冀教版九年级上册24.3 一元二次方程根与系数的关系备课ppt课件

这是一份冀教版九年级上册24.3 一元二次方程根与系数的关系备课ppt课件，共24页。PPT课件主要包含了复习回顾，课时导入，知识点，一起探究，练一练等内容，欢迎下载使用。

1.理解一元二次方程根与系数的关系，运用根与系数的关系，已知方程的一个根，求方程的另一个根及待定系数，以及根据方程求代数式的值.2.经历探索发现一元二次方程根与系数的关系，感受不完全归纳验证及演绎证明.3.提升观察、分析和综合判断的能力，勇于探索的精神.
1.解一元二次方程的方法有几种?2.如何选择解一元二次方程的方法?
格格和同学们打赌，她有一手绝活，只要同学给出两个数，她就能马上说出以这两个数为根的一元二次方程，同学们表示不相信，菲菲首先发难，恨不得考倒格格，她报的数是3，4，格格的解答是x2－7x＋12=0．菲菲验证了一下正确，接着同学们纷纷报数，格格快速准确解答．同学想不不通为什么她能快速回答，聪明的同学，你知道“源头”何在．
一元二次方程根与系数的关系
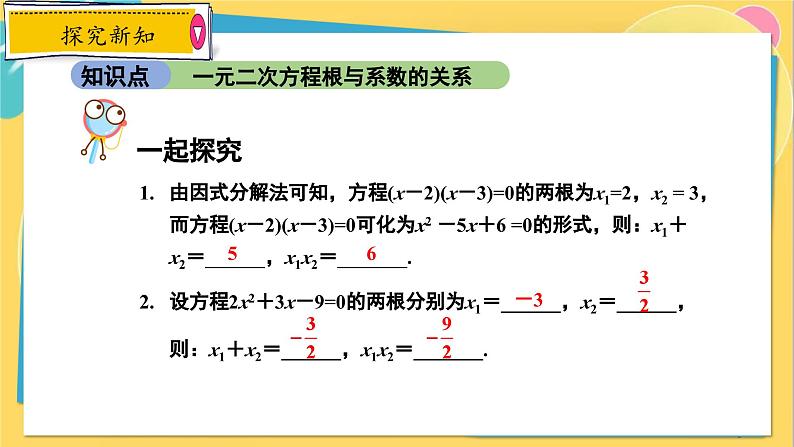
由因式分解法可知，方程(x－2)(x－3)=0的两根为x1=2，x2 = 3，而方程(x－2)(x－3)=0可化为x2 －5x＋6 =0的形式，则：x1＋x2＝______，x1x2＝_______.设方程2x2＋3x－9=0的两根分别为x1＝______，x2＝______，则：x1＋x2＝______，x1x2＝_______.
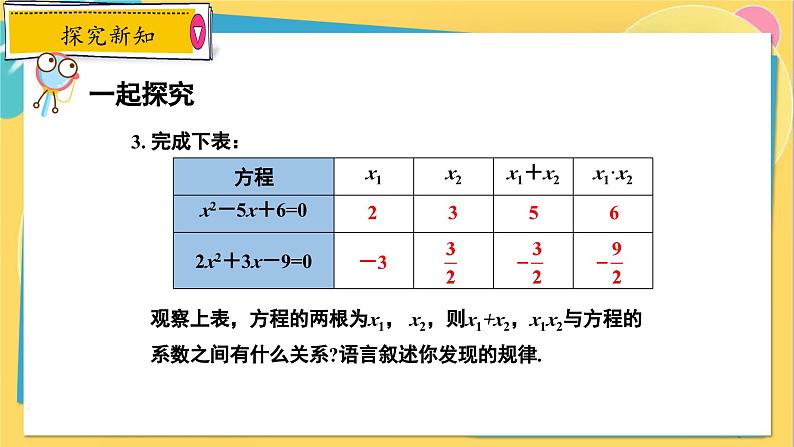
观察上表，方程的两根为x1， x2，则x1+x2，x1x2与方程的系数之间有什么关系?语言叙述你发现的规律.
4. 对于一元二次方程ax2＋bx＋c = 0，当b2－4ac≥0时，设方程的两根分别为x1，x2，请你猜想x1＋x2 ，x1x2与方程系数之间的关系，并利用求根公式验证你的结论.
1.用求根公式求解一元二次方程ax2+bx+c=0(a≠0)的两根是什么?2.分别计算x1+x2和x1·x2的值.3.归纳你验证得到的结论.
根据求根公式，得
一元二次方程根与系数的关系如果一元二次方程ax2＋bx＋c = 0的两根分别为x1，x2，那么
特别提醒：一元二次方程根与系数的关系存在的前提是a ≠ 0，b2-4ac ≥ 0.
根据一元二次方程的根与系数的关系，求 下列方程两个根的和与积： (1) x2－3x－8＝0 (2) 3x2＋4x－7＝0；
(1) 这里a＝1，b＝－3，c＝－8，且 b2－4ac＝(－3)2－4×1×(－8)＝41＞0. 所以　　　　　
(2) 3x2＋4x－7＝0；
(2) 这里a＝3，b＝4，c＝－7，且 b2－4ac＝42－4×3×(－7)＝100＞0， 所以　　　　　
求一元二次方程两根的和与积时，先要将方程整理成一般形式，然后利用根与系数的关系求出两根的和与积．
一元二次方程x2＋4x－3＝0的两根为x1，x2，则x1·x2的值是(　　)A．4　　 　B．－4　　 　C．3　 　 D．－3已知x1、x2是方程x2＋3x－1＝0的两个实数根，那么下列结论正确的是(　　)A．x1＋x2＝－1 B．x1＋x2＝－3C．x1＋x2＝1 D．x1＋x2＝3
一元二次方程的根与系数的关系的应用
已知关于x的方程x2－6x＋p2－2p＋5＝0的一个根是2，求方程的另一个根和p的值．点拨：已知二次项系数与一次项系数，利用两根之和可求出另一根，再运用两根之积求出常数项中p的值．
解： 设方程的两根为x1和x2， ∵x1＋x2＝ ＝ 6，x1＝2，∴x2＝4.　 又∵x1x2＝ ＝p2－2p＋5＝2×4＝8， ∴p2－2p－3＝0，解得 p＝3或p＝－1.　　　　
已知方程的一根求另一根：方法一：可以直接代入先求方程中待定字母的值，然后再解方程求另一根．方法二：可以直接利用根与系数的关系求另一根及待定字母的值．
方程已知关于x的一元二次方程x2＋(m＋3)x＋m＋1＝0的两个实数根为x1，x2，若x12＋x22＝4，则m的值为___________．
根据题意可得x1＋x2＝－m－3，x1x2＝m＋1，∵x12＋x22＝(x1＋x2)2－2x1x2，∴(－m－3)2－2(m＋1)＝4，解得m1＝－1，m2＝－3，并且当m＝－1或m＝－3时方程都有解，∴m的值为－1或－3.
已知方程两根的关系求待定字母系数（或代数式）的值，将两根的和与积整体代入求解.特别提醒：在解题时，注意完全平方公式及平方差公式的逆应用.
若关于x的一元二次方程x2－3x＋p＝0(p≠0)的两个不相等的实数根分别为a和b，且a2－ab＋b2＝18，则 ＋ 的值是(　　)A．3 B．－3 C．5 D．－5
若关于x的一元二次方程x2＋kx＋4k2－3＝0的两个实数根分别是x1，x2，且满足x1＋x2＝x1x2，则k的值为(　　)A．－1或　　 B．－1　　 C.　 　 D．不存在
等腰三角形三边长分别为a，b，2，且a，b是关于x的一元二次方程x2－6x＋n－1＝0的两根，则n的值为(　　)A．9　　　 B．10　　　C．9或10　　　 D．8或10
1．[2022·益阳]若x＝－1是方程x2＋x＋m＝0的一个根，则此方程的另一个根是(　　)A．－1 B．0C．1 D．2
2．[2023·乐山]若关于x的一元二次方程x2－8x＋m＝0的两根为x1，x2，且x1＝3x2，则m的值为(　　)A．4 B．8C．12 D．16