冀教版九年级上册25.6 相似三角形的应用示范课课件ppt

这是一份冀教版九年级上册25.6 相似三角形的应用示范课课件ppt，共27页。PPT课件主要包含了知识点，利用影子测高度，大纲设计的方案，利用工具测高度，利用镜子反射测高度，常见的测量方式等内容，欢迎下载使用。

1.能够利用相似三角形的知识，求出不能直接测量的物体的高度;2.在解决实际问题的过程中，进一步理解相似三角形的判定和性质，发展应用意识；3.培养学生的动手操作能力和交流与合作的意识，积累数学活动经验.
埃及金字塔到底有多高?
据史料记载：古希腊科学家泰勒斯利用相似三角形的原理，借助金字塔在太阳光线下形成的影子测出了金字塔的高度．你知道他是怎样测量的吗?
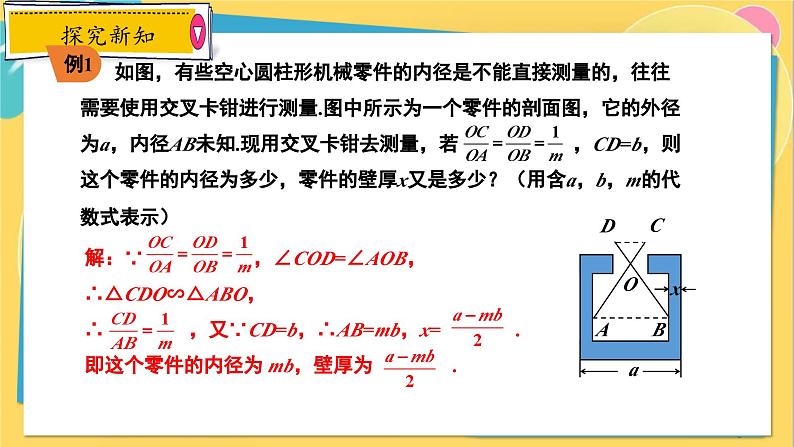
如图，有些空心圆柱形机械零件的内径是不能直接测量的，往往需要使用交叉卡钳进行测量.图中所示为一个零件的剖面图，它的外径为a，内径AB未知.现用交叉卡钳去测量，若 ，CD=b，则这个零件的内径为多少，零件的壁厚x又是多少？（用含a，b，m的代数式表示）
思考1.通过阅读题目，将实际问题可以转化为什么数学问题?
2.由已知 ，能得到两个三角形相似吗？
（根据两边成比例且夹角相等的两个三角形相似可得.)
3.根据三角形相似，能得到和内径AB有关的比例式吗?
（ ）
4.根据以上比例式，能否求出内径AB的长？根据图形能否求出壁厚x的值？
解：∵ ，∠COD=∠AOB，∴△CDO∽△ABO，∴ ，又∵CD=b，∴AB=mb，x= .即这个零件的内径为 mb，壁厚为 .
　　对于学校里旗杆的高度，我们是无法直接进行测量的．但是我们可以根据相似三角形的知识，测出旗杆的高度．结合下面图形大家思考如何求出高度？
(1)请设计一个测量旗杆高度的方案，说明理由，并与大家交流.(2)思考下面“大纲设计的方案”是否可行.如果可行，请说明其中的道理，若标杆CD=2 m，标杆影子BD=3 m，旗杆影子BO=12 m，求旗杆的高.
点拨：利用阳光下的影子测高：(1)构造相似三角形，如图.(2)测量数据：AB(身高)，BC(人影长)，BE(旗杆影长)；待求数据：DE(旗杆高)．(3)计算理由： 因为AC∥DB(平行光)，所以∠ACB＝∠DBE.∵∠ABC＝∠DEB＝90°(直立即为垂直)，∴△ABC∽△DEB，有
如图，在阳光下的某一时刻，将一根标杆CD竖立在旗杆影子上，使标杆的影子BD落在旗杆的影子BO上，且它们影子的顶端重合. 这时，量一量CD，BD，BO的长，可得旗杆AO的长为
大刚方案的设计方案可行.利用标杆与旗杆平行，得到两个三角形相似.旗杆的高为： =8 m.
1.测量方法：测量不能到达顶部的物体的高度时，常常利用光线构造相似三角形，利用相似三角形对应边的比相等列出关于物高、物影、人高、人影的比例关系式：物高：人高=物影：人影，然后通过测量物影、人高、人影来计算出物高．
2.要点精析：(1)由于太阳在不停地移动，影子的长也随着太阳的移动而发生变化．因此，测量影子的长一定要在同一时刻下进行，否则就会影响结果的准确性．(2)太阳离我们非常远，因此可以把太阳光线近似地看成平行光线．(3)此方法要求被测物体的底部可以到达，否则测不到被测物体的影长，从而计算不出物体的高．
解：过点C作CE⊥AB于点E，因此BE＝CD＝1.2 m，CE＝BD＝2.7 m，由 可得AE＝3 m，所以AB＝AE＋BE＝1.2＋3＝4.2 m.∴这棵树的高度为4.2 m.
小明想利用树影测量树高，他在某一时刻测得长为1 m的竹竿影长0.9 m，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上，如下图，他先测得留在墙上的影高1.2 m，又测得地面部分的影长2.7 m，他求得的树高是多少?
如图所示，王刚同学所在的学习小组欲测量校园里一棵大树的高度，他们选王刚作为观测者，并在王刚与大树之间的地面上直立一根高为2 m的标杆CD，然后，王刚开始调整自己的位置，当他看到标杆的顶端C与树的顶端E重合时，就在该位置停止不动，这时其他同学通过测量，发现王刚的脚离标杆底部的距离为1 m，离大树底部的距离为9 m，王刚的眼离地面的高度AB为1.5 m，那么大树EF的高为多少？
解：作AH⊥EF于H，AH交CD于G点，如图，易得BD=1，BF=9，∵DG=HF=AB=1.5，AG=BD=1，∴CG=CD－DG=2－1.5=0.5，∵CG∥EH，∴△ACG∽△AEH，∴ ，即 ，解得EH=4.5，∴EF=EH＋FH=4.5＋1.5=6（m），即大树EF的高为6 m.
　　若在一个阴天，没有太阳光，还能测量金字塔的高度吗?　
　　用镜面反射测量高度，如下图，点A是个小镜子，根据光的反射定律：由入射角等于反射角构造相似三角形．
点拨：根据光的反射定律由入射角等于反射角构造△AOB与△AFE相似，即可利用对应边的比相等求出BO.
利用相似三角形测量的一般步骤：(1)构造：利用平行线、标杆等构造相似三角形；(2)测量：测量与表示未知量的线段相对应的边长以及另外任意一组对应边的长度；(3)计算：画出示意图，利用相似三角形的性质，列出以上包括未知量在内的四个量的比例式，解出未知量，并得出答案．
如图所示，小丽为了测量高楼MN的高度，在离N点20 m的A处放了一个平面镜，小丽沿NA方向向后退到C点，正好从镜中看到楼顶M点．若AC等于1.5 m，小丽的眼睛离地面的高度BC为1.6 m，请你帮助小丽计算一下此楼的高度(精确到0.1m)．
解：如图，过点A作OA⊥CN，∵BC⊥CA，MN⊥NA，∴∠BCA＝∠MNA＝90°.又∵∠BAO＝∠MAO，∴∠BAC＝∠MAN.∴△BCA∽△MNA.∴MN≈21.3 m.即此楼的高度约为21.3 m.
如图所示，这是大家都做过的“小孔成像”实验示意图. 已知蜡烛与光屏之间的距离为l. 具有“小孔”的纸板放在什么位置时，蜡烛火焰的高度AB是它的像B'A'的高度的一半?
泰勒斯是怎样测量金字塔的高度？如图，木杆EF长2 m，它的影长FD为4 m，测得OA为274 m，求金字塔的高度BO．
解：太阳光是平行光线，因此∠BAO=∠EDF.
又∠AOB=∠DFE=90°，∴△ABO∽△DEF.
1．古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔影子的顶部直立一根木杆，借助太阳光测金字塔的高度．如图，木杆EF长2 m，它的影长FD是4 m，同一时刻测得OA是268 m，则金字塔的高度BO是_______m.
2．[2023·南充]如图，数学活动课上，为测量学校旗杆高度，小菲同学在脚下水平放置一平面镜，然后向后退(保持脚、镜和旗杆底端在同一直线上)，直到她刚好在镜子中看到旗杆的顶端．已知小菲的眼睛离地面高度为1.6 m，同时量得小菲与镜子的水平距离为2 m，镜子与旗杆的水平距离为10 m，则旗杆高度为(　　)A．6.4 m B．8 m C．9.6 m D．12.5 m