冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt

这是一份冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt，共34页。PPT课件主要包含了与测量有关的术语，巩固概念，知识点，坡度的应用，实际问题，数学模型，感悟新知，坡角的应用等内容，欢迎下载使用。

1.结合实际问题情境认识坡度、坡角等与测量有关的的术语，弄清它们的意义.2.能用解直角三角形的相关知识去解决一些简单的与坡度、坡角有关的实际问题.3.学会将实际问题抽象成数学问题，从而进一步把形和数结合起来，提高分析和解决问题的能力，进一步感受数学与实际生活的联系.
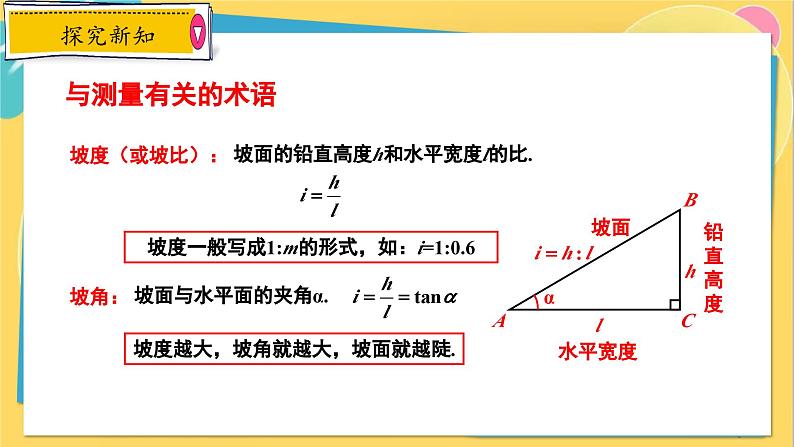
在筑坝、开渠、挖河和修路等图纸上都要注明斜坡的倾斜程度.
在筑坝、开渠、挖河和修路时，设计图上都要注明斜坡的倾斜程度.
坡面的铅直高度h和水平宽度l的比.
坡度一般写成1:m的形式，如：i=1:0.6
坡度越大，坡角就越大，坡面就越陡.
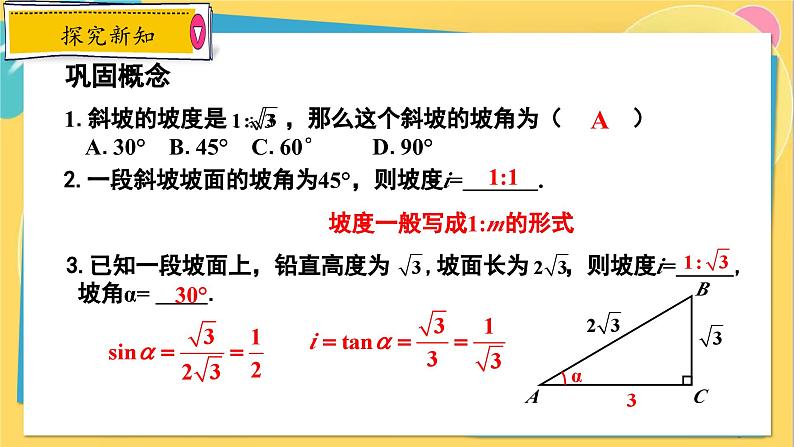
1.斜坡的坡度是 ，那么这个斜坡的坡角为（ ） A.30° B.45° C.60° D.90°
2.一段斜坡坡面的坡角为45°，则坡度i= .
坡度一般写成1:m的形式
如图所示，铁路路基的横断面为四边形ABCD，其中， BC∥AD，∠A＝∠D，根据图中标出的数据计算路基下底的宽和坡角(结果精确到1′).
(1)进行和坡度有关的计算，常作辅助线构造直角三角形，根据解直角三角形的知识求坡角.
(2)根据坡度概念及梯形的高，可以求出AE，DF的长.
(3)由矩形的性质可得EF与BC的数量关系，求出EF的长，从而求出底AD的长. (AD=AE+EF+DF)
(4)在Rt△ABE中，由坡角和坡度之间的关系可求出坡角.
如图，作BE⊥AD，CF⊥AD，垂足分别为E，F. 在四边形BEFC中，∵BC∥AD, ∠AEB=∠DFC=90°,∴四边形BEFC为矩形. ∴BC=EF，BE=CF.
在 Rt△ABE 和 Rt△DCF中，∵∠A=∠D， ∠AEB=∠DFC, BE=CF,∴Rt△ABE≌Rt△DCF.∴AE=DF.
在 Rt△ABE中，∴∠α=38°39′，AE=5.∴ AD=AE＋EF＋FD=BC＋2AE=10＋2×5 = 20. 即路基下底的宽为20 m，坡角约为38°39′.
1. 坡度是两条线段的比值，不是度数.2. 表示坡度时，通常把比的前项取作1，后项可以是小数.3. 物体的倾斜程度通常可用物体的坡度表示，坡度越大，坡角越大，坡面越陡；反之，坡度越小，坡角越小，坡面越缓.
如图，设他升高了h m， ∵i＝ BC＝h m， ∴AC＝2h m. 由BC2＋AC2＝AB2， 得h2＋(2h)2＝1 0002， ∴h2＝2×105，即h＝200
小明沿着坡比为1∶2的山坡向上走了1 000 m，则 他升高了(　　) A．200 m　 B．500 m　 C．500 m　 D．1 000 m
一个长方体木箱沿斜面下滑，当木箱滑至如图所示的位置时，AB＝3 m，已知木箱高BE＝ m，斜面坡角为30°，求木箱端点E距地面AC的高度EF.
连接AE，在Rt△ABE中求出AE，且根据∠EAB的正切值求出∠EAB的度数，进而得到∠EAF的度数，最后在Rt△EAF中解出EF即可．
连接AE，如图所示．在Rt△ABE中，AB＝3，BE＝ 则AE＝∵tan ∠EAB＝ ∴∠EAB＝30°.
在Rt△AEF中，∠EAF＝∠EAB＋∠BAC＝30°＋30°＝60°，∴EF＝AE×sin ∠EAF＝答：木箱端点E距地面AC的高度EF为3 m.
如图，一居民楼底部B与山脚P位于同一水平线上，小李在P处测得居民楼顶A的仰角为60°，然后他从P处沿坡角为45°的山坡向上走到C处，这时，PC＝30 m，点C与点A在同一水平线上，A，B，P，C在同一平面内． (1)求居民楼AB的高度； (2)求C，A之间的距离． (结果精确到0.1 m，参考数据： ≈1.41， ≈1.73， ≈2.45)
(1)过点C作CE⊥BP，交BP的延长线于点E， 易知AB＝EC. 在Rt△CPE中，由sin ∠CPE＝ 得出EC的长度，进而可求出答案．(2)在Rt△ABP中， 由tan ∠APB＝ 得出BP的长， 在Rt△CPE中， 由cs ∠CPE＝ 得出PE的长， 最后由AC＝BE＝BP＋PE得出答案．
(1)过点C作CE⊥BP，交BP的延长线于点E，易得AB＝CE. 在Rt△CPE中，PC＝30 m，∠CPE＝45°， ∵sin ∠CPE＝ ∴CE＝PC·sin ∠CPE＝30× ≈21.2(m)． ∴AB＝CE≈21.2 m.即居民楼AB的高度约为21.2 m.
(2)在Rt△ABP中，AB＝ m，∠APB＝60°， ∴BP＝ 在Rt△CPE中，PC＝30 m，∠CPE＝45°， ∴PE＝PC·cs ∠CPE＝30× 易得AC＝BE＝BP＋PE ＝5 ＋15 ≈33.4(m)， 即C，A之间的距离约为33.4 m．
修建一条铁路要经过一座高山，需在山腰B处开凿一条隧道BC.经测量，西山坡的坡度i=1:0.6，由山顶A观测到点C的俯角为60°，AC的长为60 m，如图所示，试求隧道BC的长（结果精确到0.1m).
作AD⊥BC于D，在Rt△ADC中求出AD、DC，在Rt△ABD中，根据∠ABD的正切值求出BD，进而得到BC的长．
解：如图，作AD⊥BC于点D.
∵A对山坡C处的的俯角为60°，
答：隧道BC的长约为61.2m.
1．[2023·宁夏]如图，粮库用传送带传送粮袋，大转动轮的半径为10 cm，传送带与水平面成30°角，假设传送带与转动轮之间无滑动，当大转动轮转140°时，传送带上点A处的粮袋上升的高度是________cm(传送带厚度忽略不计)．
【点拨】如图，设传送带上点A处的粮袋上升到点B，过点A作MN的平行线，过点B作MN的垂线，两线交于点C.易知△ABC为直角三角形．
2．[2023·连云港]渔湾是国家“AAAA”级风景区，图①是景区游览的部分示意图．
如图②，小卓从九孔桥A处出发，沿着坡角为48°的山坡向上走了92 m到达B处的三龙潭瀑布，再沿坡角为37°的山坡向上走了30 m到达C处的二龙潭瀑布．小卓从A处的九孔桥到C处的二龙潭瀑布上升的高度DC约为________m. (结果精确到0.1 m)(参考数据：sin 48°≈0.74，cs48°≈0.67，sin 37°≈0.60，cs 37°≈0.80)