九年级上册26.4 解直角三角形的应用背景图ppt课件

这是一份九年级上册26.4 解直角三角形的应用背景图ppt课件，共30页。PPT课件主要包含了知识回顾，知识点，感悟新知等内容，欢迎下载使用。

1.能根据题意画出数学问题的示意图.2.利用相关的解直角三角形的知识来测量与计算高大建筑物的高度.3.通过审题，借助锐角三角函数等内容建立方程，提高分析和解决问题的能力，提高学习数学的兴趣和应用意识.
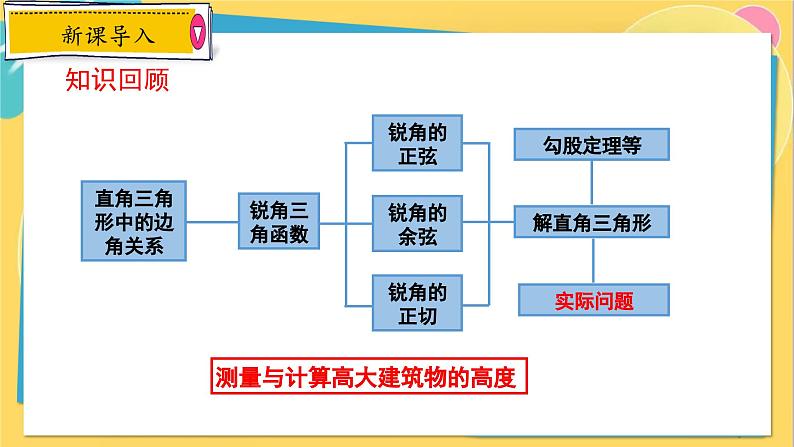
测量与计算高大建筑物的高度
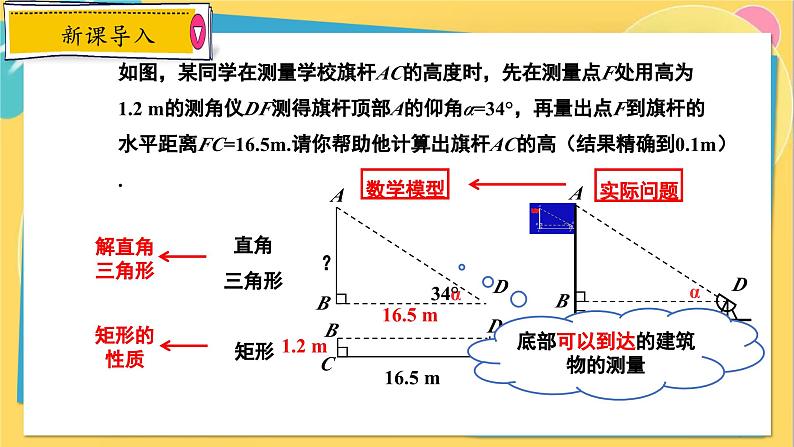
底部可以到达的建筑物的测量
底部不可以到达的高大建筑物的测量
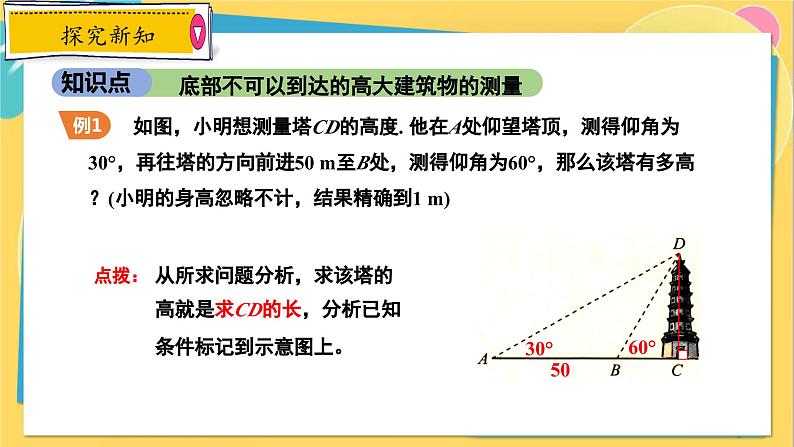
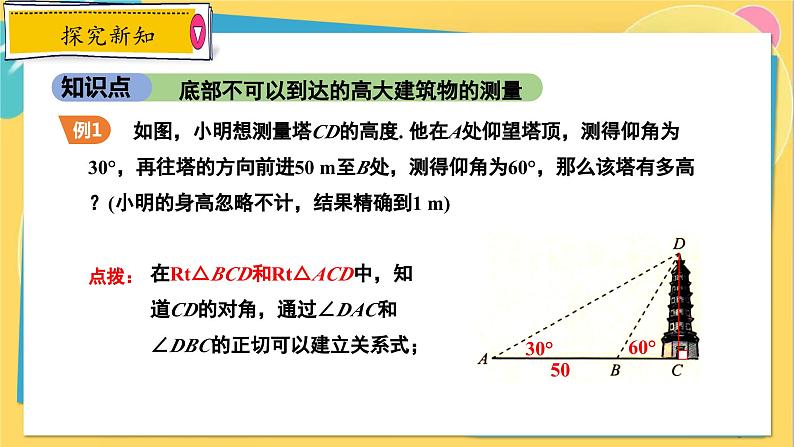
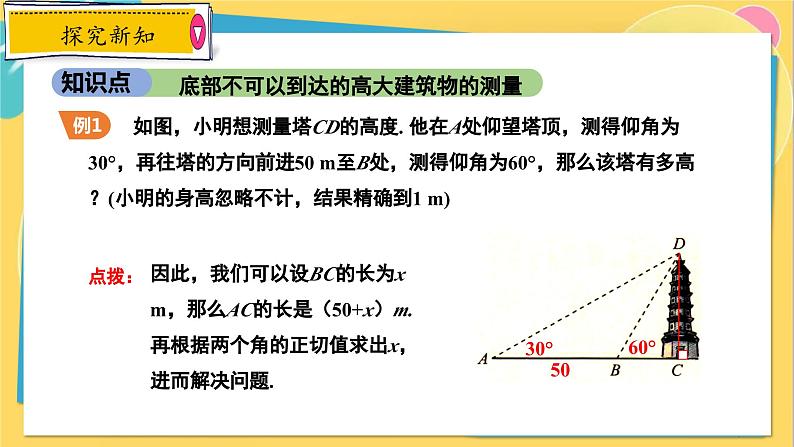
如图，小明想测量塔CD的高度. 他在A处仰望塔顶，测得仰角为30°，再往塔的方向前进50 m至B处，测得仰角为60°，那么该塔有多高？(小明的身高忽略不计，结果精确到1 m)
从所求问题分析，求该塔的高就是求CD的长，分析已知条件标记到示意图上。
在Rt△BCD和Rt△ACD中，知道CD的对角，通过∠DAC和∠DBC的正切可以建立关系式；
因此，我们可以设BC的长为x m，那么AC的长是（50+x）m.再根据两个角的正切值求出x，进而解决问题.
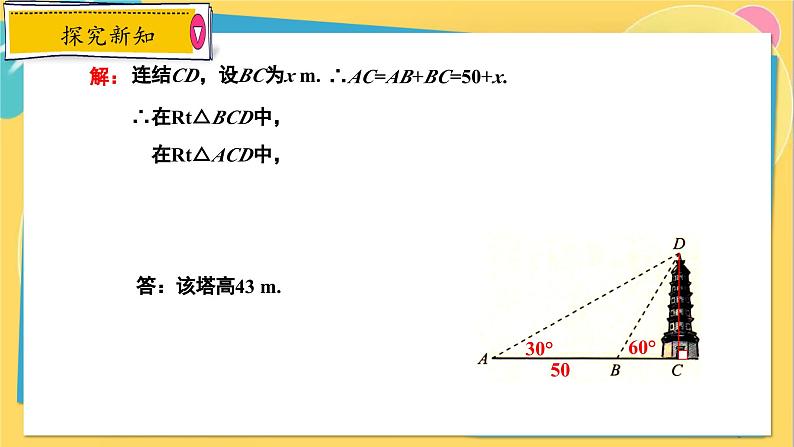
连结CD，设BC为x m.
在Rt△ACD中，
∴AC=AB+BC=50+x.
∴△ABD是等腰三角形，BD=AB=50.
在Rt△BCD中，
∵∠DBC=60°，∠DAB=30°，∴∠ADB=30°
运用锐角三角函数解决实际问题的方法： (1)弄清题意，画出示意图；(2)找出图形中的线段、角所表示的实际意义，并找到所要 解决的问题；(3)寻找要求解的直角三角形，有时需要作适当的辅助线；(4)选择合适的边角关系式，进行有关锐角三角函数的计算；(5)按照题目要求的精确度确定答案，并注明单位，作答．
在数学活动课上，老师带领学生去测量位于北京大学未名湖东南湖畔的博雅塔的高度.
在数学活动课上，老师带领学生去测量位于北京大学未名湖东南湖畔的博雅塔的高度.如图，在C处用高1.2m的测角仪CE测得塔顶A的仰角为30°，向塔的方向前进50 m到达D处，在D处测得塔顶A的仰角为71°.求博雅塔的高AB约为多少米（结果精确到1 m）.
从所求问题分析，求博雅塔的高就是求AB的长，我们将AB的长分成两部分来求，延长EF交AB于点G，AB的长就等于AG加BG. 边分析已知条件边标记图形.
由题意可得，四边形EFDC是矩形，四边形FGBD也是矩形，所以DF=BG=CE.CE的长1.2m，根据矩形的性质，EF=CD=50，BG=1.2，现在只需求AG即可！
图中一共有两个直角三角形，即Rt△AEG和Rt△AFG，这两个直角三角形，角度都可以求出来，但是因为没有直接给出的已知边长，所以Rt△AEG和Rt△AFG，都是不可以直接求解的.
我们关注到这两个直角三角形有一条公共边AG，因为知道锐角的角度，所以边之间的比值，能通过三角函数建立关系从而转化.
所以可以设AG为x m.那么其它边都可以用含x的代数式表示，再根据EG－FG=EF=50，得到关于x的方程，进而求得x的值，从而解决问题.
设EF的延长线交AB于点G，根据题意得， DF=BG=CE=1.2，EF=CD=50.设AG为x m. 在Rt△AEG和Rt△AFG中，∵∠AEF=30°， ∠AFG=71° ，∴∠EAG=60°，∠FAG=19°.
等量关系：EG－FG=EF=50
“中国益阳”网上消息，益阳市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥．
想一想，你要怎样测量？
“中国益阳”网上消息，益阳市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥． 如图，新大桥的两端位于A，B两点，小张为了测量A，B之间的河宽，在垂直于新大桥AB的直线形道路l上测得如下数据：∠BDA＝76.1°，∠BCA＝68.2°，CD＝82 m．求 AB的长．(结果精确到0.1 m．参考数据：sin76.1°≈0.97，cs 76.1°≈0.24，tan 76.1°≈4.0；sin 68.2°≈0.93，cs 68.2°≈0.37，tan 68.2°≈2.5)
设AD＝x m，在Rt△ABC中，利用∠BCA的正切值，可以用含x的代数式表示AB.同理在Rt△ABD中，利用∠BDA的正切值表示出AB，从而列出关于x的方程，求出x的值就能求出AB的长了．
设AD＝x m，则AC＝(x＋82) m. 在Rt△ABC中，tan ∠BCA＝∴AB＝AC·tan ∠BCA＝(x＋82)tan 68.2° m. 在Rt△ABD中，tan ∠BDA＝∴AB＝AD·tan ∠BDA＝xtan 76.1° m.∴(x＋82)tan 68.2°＝xtan 76.1°.∴x≈136.67.∴AB≈4×136.67≈546.7(m)． 即AB的长约为546.7 m.
解直角三角形的应用问题，需要把实际问题转化为数学模型来解决． 解决直角三角形有关的应用题最常用的方法是画图(包括作辅助线，构造直角三角形或特殊平行四边形)，根据所给数据，选用恰当的锐角三角函数求出有关的量或用含有未知数的式子表示有关的量进行求解． 警示点： (1)注意方程思想的运用； (2)注意结果必须根据题目要求进行保留．
如图，一幢楼房AB背后有一台阶CD，台阶每层高0.2 m，且AC＝17.2 m，设太阳光线与水平地面的夹角为α，当α＝60°时，测得楼房在地面上的影长AE＝10 m，现有一只小猫睡在台阶的MN这层上晒太阳( 取1.73)．(1)求楼房的高度约为多少米．(2)过了一会儿，当α＝45°时，问小猫还能否晒到太阳？请说明理由．
(1)当α＝60°时，在Rt△ABE中， ∵tan 60°＝ ∴AB＝10·tan 60°＝10 ≈10×1.73＝17.3(m)． 即楼房的高度约为17.3 m.
假设没有台阶，当α＝45°时，从点B射下的光线与地面AD的交点为点F，与射线CM的交点为点H(如图)．
(2)过了一会儿，当α＝45°时，问小猫还能否晒到太阳？请说明理由．
∵∠BFA＝45°， ∴tan 45°＝ ＝1，此时的影长AF＝AB≈17.3m． ∴CF＝AF－AC≈17.3－17.2＝0.1(m)．∴CH＝CF≈0.1 m． ∴大楼的影子落在台阶MC这个侧面上， ∴小猫仍可以晒到太阳．
1．[2023·河南]综合实践活动中，某小组用木板自制了一个测高仪测量树高，测高仪ABCD为正方形，AB＝ 30 cm，顶点A处挂了一个铅锤M.如图是测量树高的示意图，测高仪上的点D，A与树顶E在―条直线上，铅垂线AM交BC于点H.经测量，点A距地面1.8 m，到树EG的距离AF＝11 m，BH＝20 cm.求树EG的高度(结果精确到0.1 m ) .
2．[2023·鞍山]某商店窗前计划安装如图①所示的遮阳篷，其截面图如图②所示，在截面图中，墙面BC垂直于地面CE，遮阳篷与墙面连接处点B距地面高3 m，即BC＝3 m，遮阳篷AB与窗户所在墙面BC垂直，即∠ABC＝∠BCE＝90°，