冀教版九年级上册28.3 圆心角和圆周角集体备课ppt课件

这是一份冀教版九年级上册28.3 圆心角和圆周角集体备课ppt课件，共20页。PPT课件主要包含了知识点，圆内接四边形，圆内接四边形的性质，几何语言，°或150°等内容，欢迎下载使用。

1.掌握并能灵活运用“同弧（等弧）所对的圆周角相等”.2.理解圆内接四边形的概念.探究、掌握、并能灵活运用圆内接四边形的性质.
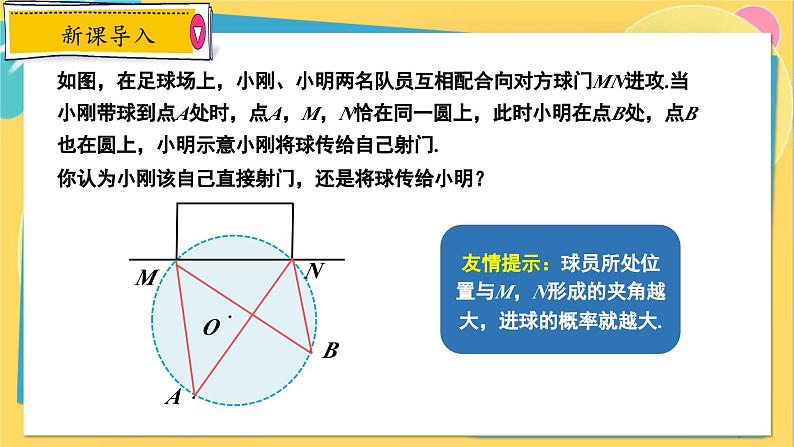
如图，在足球场上，小刚、小明两名队员互相配合向对方球门MN进攻.当小刚带球到点A处时，点A，M，N恰在同一圆上，此时小明在点B处，点B也在圆上，小明示意小刚将球传给自己射门.你认为小刚该自己直接射门，还是将球传给小明？
友情提示：球员所处位置与M，N形成的夹角越大，进球的概率就越大.
同弧（等弧）所对的圆周角相等
如图，∠ACB与∠ADB分别为⊙O上同一条弧AB所对的两个圆周角.(1)∠ACB与∠ADB之间具有怎样的大小关系？把你的猜想和大家进行交流.(2)试证明你的猜想.
解：（1）∠ACB=∠ADB;(2)证明：连接OA、OB，
∵∠ACB= ∠AOB，∠ADB= ∠AOB，
∴∠ACB=∠ADB.
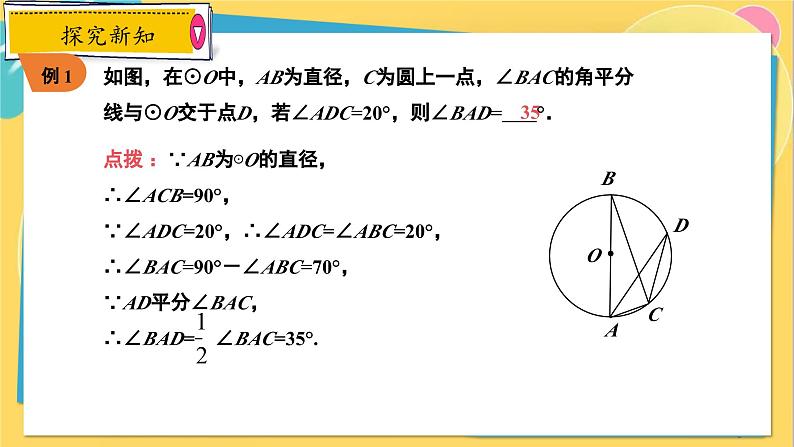
如图，在⊙O中，AB为直径，C为圆上一点，∠BAC的角平分线与⊙O交于点D，若∠ADC=20°，则∠BAD= °．
点拨 ：∵AB为⊙O的直径，∴∠ACB=90°，∵∠ADC=20°，∴∠ADC=∠ABC=20°，∴∠BAC=90°－∠ABC=70°，∵AD平分∠BAC，∴∠BAD= ∠BAC=35°.
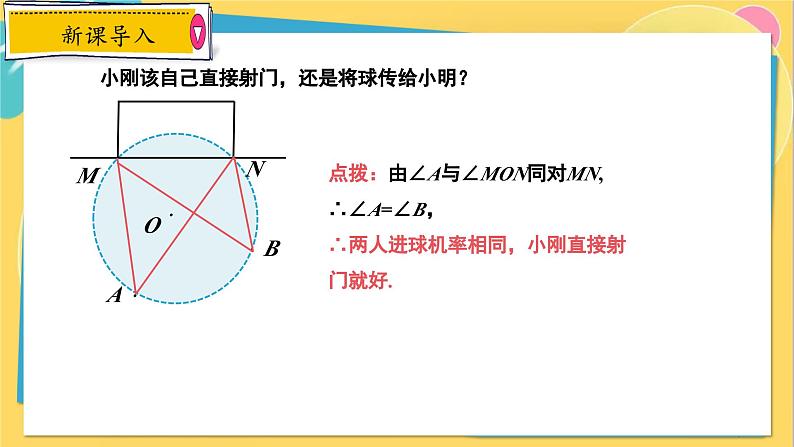
点拨：由∠A与∠MON同对MN,∴∠A=∠B，∴两人进球机率相同，小刚直接射门就好.
小刚该自己直接射门，还是将球传给小明？
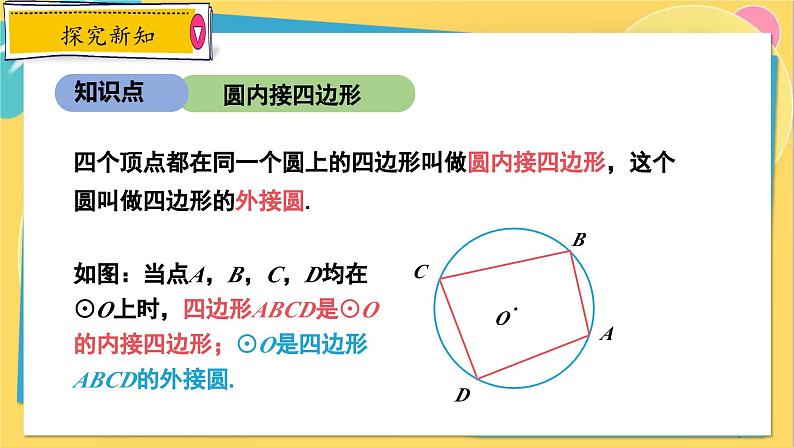
如图：当点A，B，C，D均在⊙O上时，四边形ABCD是⊙O的内接四边形；⊙O是四边形ABCD的外接圆.
四个顶点都在同一个圆上的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.
如图，四边形ABCD为⊙O的内接四边形.(1) 和 所对的圆心角之和等于多少度？∠ABC和∠ADC之间具有怎样的关系？(2)∠BAD和∠BCD之间具有怎样的关系？提出你的猜想，并和大家进行交流.
我们发现：圆内接四边形的对角互补. 下面我们对它进行证明.已知：如图，四边形ABCD为⊙O的内接四边形. 求证：∠BCD+∠BAD= 180°， ∠ABC+∠ADC= 180°.
证明：如图，连接OB，OD. ∵ 与 所对的圆心角之和为360°， ∠BCD和∠BAD分别为 和 所对的圆周角， ∴∠BCD+∠BAD= 180°. 同理可证，∠ABC+∠ADC=180°.
圆内接四边形的对角互补.
∵四边形ABCD是⊙O的内接四边形，∴∠A+∠C=180°.
如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC=130°，连接AC，则∠BAC的度数为 ．
点拨：∵四边形ABCD内接于⊙O，∠ADC=130°， ∴∠B=180°－∠ADC=180°－130°=50°， ∵AB为⊙O的直径， ∴∠ACB=90°， ∴∠BAC=90°－∠B=90°－50°=40°.
如图所示，已知四边形ABCD为☉O的内接四边形，∠DCE为四边形ABCD的一个外角. 求证∠DCE=∠BAD.
证明：∵四边形ABCD为☉O的内接四边形，
∴∠BAD+∠BCD=180°.
∵∠BCD+∠DCE=180°，
∴∠DCE=∠BAD.
圆内接四边形的外角等于它的内对角.
已知⊙O的弦AB的长等于⊙O的半径，则此弦AB所对的圆周角的度数为 ___________.
弦所对的弧有两段因此弦所对的圆周角有两种
(1)在求圆中的某一个圆周角时，根据“圆内接四边形的对角互补”，可以转化为求其所在的内接四边形的对角的度数． (2)圆内接四边形的一组对角其实是圆中一条弦所对的两类圆周角．
3．[2023·淮安]如图，四边形ABCD是⊙O的内接四边形，BC是⊙O的直径，BC＝2CD，则∠BAD的度数是________°.