初中数学冀教版八年级上册13.3 全等三角形的判定教案配套课件ppt

这是一份初中数学冀教版八年级上册13.3 全等三角形的判定教案配套课件ppt，共25页。PPT课件主要包含了BCEF，∠A∠D，∠C∠F，知识点，旋转+平移，做一做，ADE等内容，欢迎下载使用。
1. 复习并回顾全等三角形的判定方法.2. 能从图形的位置上发现两个三角形的特殊关系(平移或者旋转得到).3.会利用全等三角形的判定方法去判断两个三角形全等.
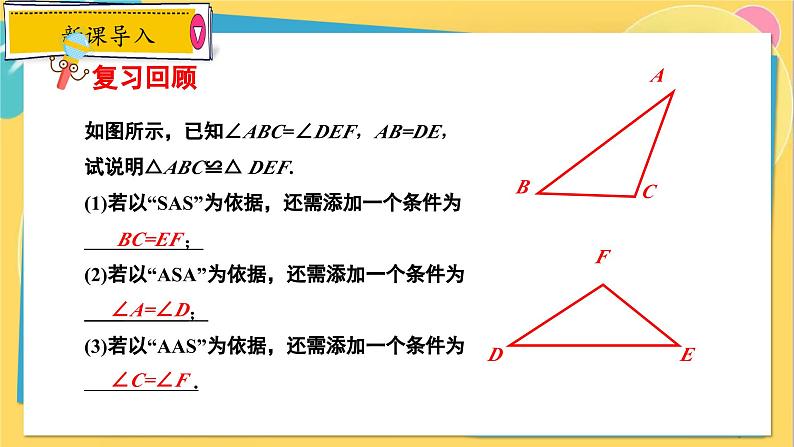
如图所示，已知∠ABC=∠DEF，AB=DE，试说明△ABC≌△ DEF.(1)若以“SAS”为依据，还需添加一个条件为　 　；(2)若以“ASA”为依据，还需添加一个条件为　　 ；(3)若以“AAS”为依据，还需添加一个条件为　 . 
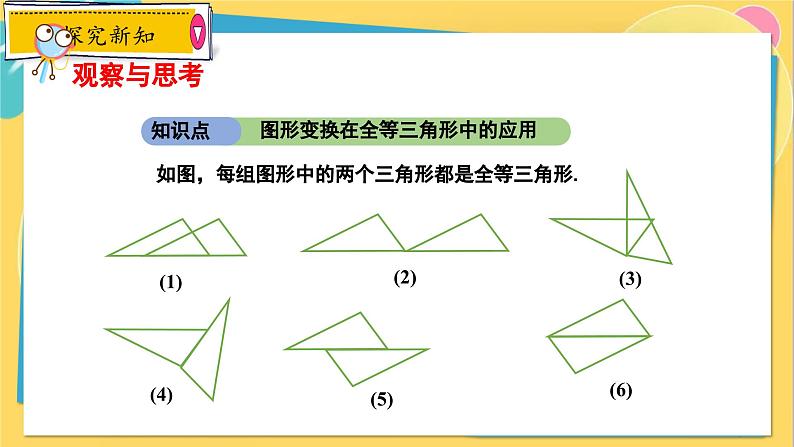
图形变换在全等三角形中的应用
如图，每组图形中的两个三角形都是全等三角形.
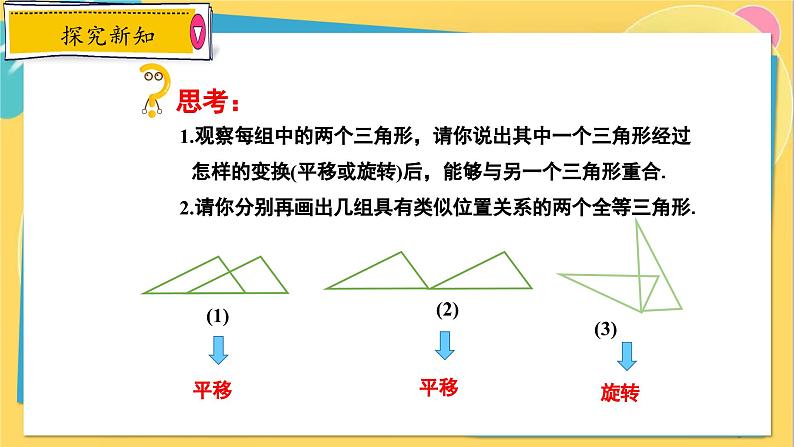
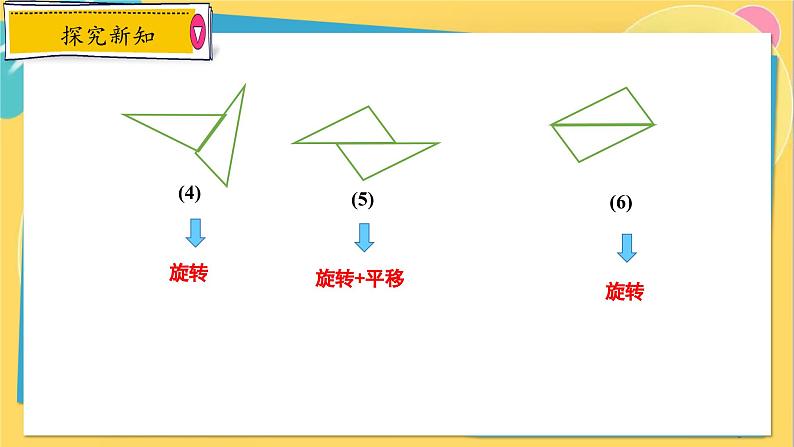
1.观察每组中的两个三角形，请你说出其中一个三角形经过怎样的变换(平移或旋转)后，能够与另一个三角形重合.2.请你分别再画出几组具有类似位置关系的两个全等三角形.
　　实际上，在我们遇到的两个全等三角形中，有些图形具有特殊的位置关系，即其中一个三角形是由另一个三角形经过平移或旋转(有时是两种变换) 得到的.发现两个三角形间的这种特殊关系，能够帮助我们找到命题证明的途径，较快地解决问题.
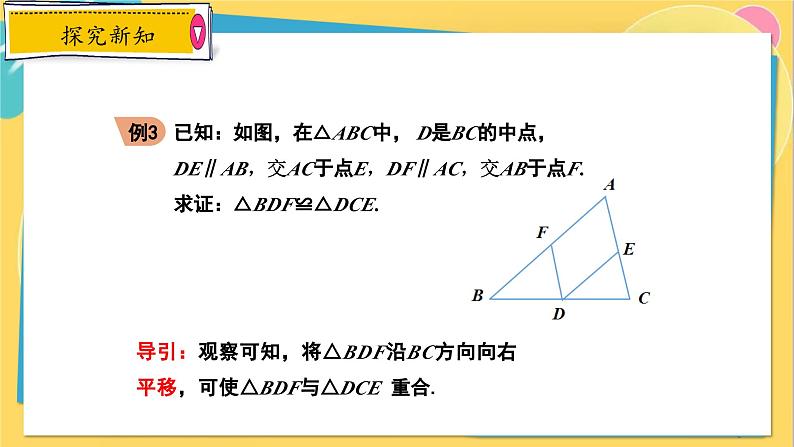
已知：如图，在△ABC中， D是BC的中点，DE∥AB，交AC于点E，DF∥AC，交AB于点F.求证：△BDF≌△DCE.
导引：观察可知，将△BDF沿BC方向向右平移，可使△BDF与△DCE 重合.
1. 已知：如图，BE = CF，AB∥ED，AC∥DF. 求证：△ABC≌△DEF.
证明：∵ AB∥ED，AC∥DF(已知)， ∴∠B =∠DEF，∠F =∠ACB(两直线平行，同位角相等). ∵ BE = CF，∴ BE + EC = CF + EC(等式的性质)，即 BC = EF. 在△ABC 和△DEF 中， ∠B =∠DEF(已证)， BC = EF(已证)， ∠ACB =∠F(已证)，∴△ABC≌△DEF (ASA).
已知：如图，在△ABC中，D，E分别是AB，AC的中点，CF∥AB，交DE 的延长线于点F.求证：DE＝FE.
导引：观察可知，将△ECF绕点E逆时针旋转180°,它可与△EAD重合.
1. 如图，在△ABC中，分别以AC，BC为边作等边三角形ACD和等边三角形BCE，连接AE，BD交于点O，则∠AOB的度数为________．
2.如图，由∠1＝∠2，BC＝DC，AC＝EC，得△ABC≌△EDC的根据是(　　)A．SAS　　　B．ASA　　　C．AAS　　　D．SSS
已知：如图，AB ∥ CD，AD∥BC. 求证：AB = CD, AD=BC.
证明：连接AC，如图：∵AB∥CD，AD∥BC(已知)，∴∠BAC＝∠DCA,∠BCA＝∠DAC,(两直线平行，内错角相等). 又∵AC=CA(公共边)，∴△ABC≌△CDA(ASA).∴AB = CD, AD=BC.
全等变换在实际中的应用
如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是(　　)A．60° B．90°C．120° D．150°
解：∵滑梯、墙、地面正好构成直角三角形，∵BC=EF，AC=DF，∴Rt△ABC≌Rt△DEF，∴∠ABC=∠DEF,∠ACB=∠DFE.∵∠DEF+∠DFE=90°.∴∠ABC+∠DFE=90°.
如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC.将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠PAE.则说明这两个三角形全等的依据是(　　)A．SASB．ASAC．AASD．SSS
两个不同点的方位角问题
1. 如图，小敏做了一个角平分仪 ABCD ，其中 AB ＝ AD ， BC ＝ DC . 将仪器上的点 A 与∠ PRQ 的顶点 R 重合，调 整 AB 和 AD ，使它们分别落在角的两边上，过点 A ， C 画一条射线 AE ， AE 就是∠ PRQ 的平分线.此角平分仪 的画图原理是：根据仪器结构，可得△ ABC ≌△ ADC ， 这样就有∠ QAE ＝∠ PAE . 则说明这两个三角形全等的 依据是(　D　)
2. 如图，∠ BAD ＝∠ CAE ， AB ＝ AD ， AC ＝ AE ，且 E ， F ， C ， D 在同一直线上.
(1)填空：观察可知，将△ ABC 绕点 逆时针旋转， 可与△ 重合.(2)求证： BC ＝ DE .
3. 如图，在四边形 ABCD 中， E ， F 分别是边 AB ， AD 上 一点， CD ＝ CE ，∠ BEC ＝∠ D ，∠ B ＋∠ AFC ＝ 180°.求证： EB ＝ DF ；