冀教版八年级上册14.1 平方根图文ppt课件

这是一份冀教版八年级上册14.1 平方根图文ppt课件，共28页。PPT课件主要包含了复习提问，引出问题，知识点，平方根的定义，做一做，平方根的性质，填写下表，求平方根开平方，大家谈谈，互为逆运算等内容，欢迎下载使用。

1. 了解数的平方根的概念，会用根号表示一个数的平方根.2. 探究平方根的性质，并能灵活运用.3. 了解开平方与平方互为逆运算，会利用这个互逆运算关系求非负数的平方根.
小明家有一块面积为100 m²的正方形花圃. 花圃周围要用护栏围起来，需要护栏多少米？
分析：要求出护栏的长，需要知道正方形的边长.求花圃的边长就是已知一个数的平方等于100，求这个数.
平方等于100的会是什么样的一个数呢？我们来探究一下吧
1. 和－ 的平方等于多少？ 10和－10的平方等于多少？
2.平方等于 的数有哪些？平方等于100的数呢？
和－ 的平方等于 , 10和－10的平方等于100.
平方等于 的数有 和－ ,平方等于100的数有10和－10.
3.满足x2 = 25的x的值是多少？
满足x2 = 25的x的值是5和-5.
感总结：平方根的定义新 一般地，如果一个数x的平方等于a，即x2=a，那么这个数x就叫做a的平方根(square rt)，也叫做a的二次方根.知
1.下列说法： ①±5是25的平方根； ②49的平方根是－7； ③8是16的平方根； ④－3是9的一个平方根． 其中正确的个数是(　　) A．1　 　B．2　 　C．3　 　D．4
2.如果x2＝a，那么下列说法错误的是(　　) A. 若x确定，则a的值是唯一的 B. 若a确定，则x的值是唯一的 C. a是x的平方 D. x是a的平方根3.4的平方根是(　　) A．±2 　B．－2　　C．2　　　D．±
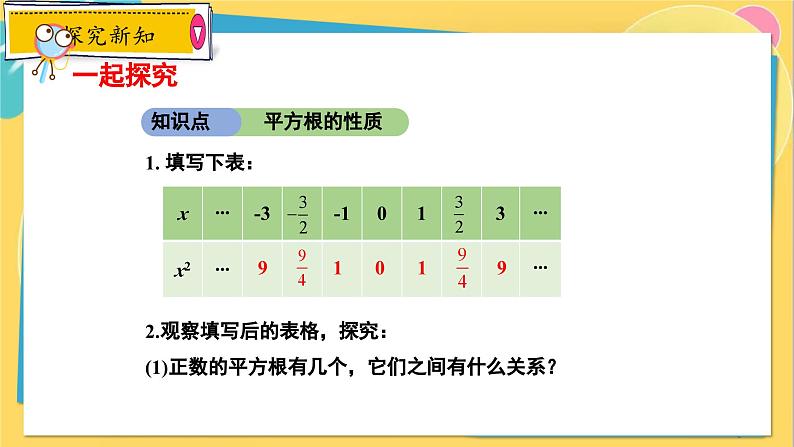
2.观察填写后的表格，探究：(1)正数的平方根有几个，它们之间有什么关系？
(2)0有平方根吗？如果有，它是什么数？ (3)负数有平方根吗？
平方根的性质：(1) 一个正数有两个平方根，它们互为相反数.
(2) 0只有一个平方根，是0本身；
(3)负数没有平方根．
平方根的表示方法： 一个正数有两个平方根：一个正数，一个负数.正数 a的正平方根用符号“ ”表示，读作“根号a”;正数a的负平方根用符号“ ”表示，读作“负根号a”.
正数a的两个平方根记为 ，其中a称为被开方数.
如4的平方根为 ，被开方数是4；0.01的平方根为 ，被开方数是0.01.
被开方数a一定是怎样的一个数？
(1)已知3＋a的平方根是±5，求a的值；(2)一个正数x的两个平方根分别是－a＋2与2a－1，求a的值和这个正数x的值．
导引：(1)由平方根的定义知3＋a等于(±5)2.
导引：(2)正数x有两个平方根，分别是－a＋2与2a－ 1，所以－a＋2与2a－1互为相反数，即－a ＋2＋2a－1＝0，解方程可求出a；根据x＝ (－a＋2)2，代入a的值可求出x的值．
解：(2)因为正数x有两个平方根， 分别是－a＋2与2a－1， 所以－a＋2+2a－1=0，解得a=－1, 所以x=
题(1)运用平方根的定义中被开方数等于它的平方根的平方列方程； 题(2)运用平方根的性质中正数的两个平方根的关系列方程，通过方程思想求相关待定字母的值是数学中常用的方法．
1.已知正数x的两个平方根分别为a＋2和2a－8，求x的值．
解：根据题意得，a＋2＋2a－8＝0，解得a＝2. 所以x＝(a＋2)2＝(2＋2)2＝42＝16.
2. 下列说法正确的有(　　) ①－2是－4的一个平方根； ②a2的平方根是a； ③2是4的一个平方根； ④4的平方根是－2. A．1个 B．2个 C．3个 D．4个
3.下列关于“0”的说法中，正确的是(　　) A．0是最小的正整数 B．0没有相反数 C．0没有倒数 D．0没有平方根
观察框图，说一说求一个数的平方运算和求一个数的平方根运算具有怎样的关系.
总结： 我们把求一个数的平方根的运算，叫做开平方.我们可以借助平方运算来求一个正数的平方根.
对于正数来说，开平方与平方互为逆运算.
求一个数a的平方根的运算，叫做开平方，其中a叫做被开方数. 平方根是一个数，是开平方的结果；开平方是和加、减、乘、除、乘方一样的一种运算，是求平方根的过程.平方和开平方互为逆运算，我们可以用平方运算来检验开平方的结果是不是正确.
求下列各数的平方根： (1)81；(2) ；(3) 0.04.
注意:平方根的通用符号是± (a≥0)，防止粗心大意漏掉“- ”而出错.
1.求下列各数的平方根： (1)16；　(2)0.49；　(3) ；　(4)－9.
(3)因为 ，所以 的平方根± ，即 (4)因为－9＜0，所以－9没有平方根．
2.下列各式正确的是(　　) A. ＝±5 B．± ＝－5 C．± ＝±5 D．± ＝5
两个不同点的方位角问题
1.36的平方根是±6的数学表达式是(　D　)
2. [母题·教材P62习题T1]填表：
3. [2023·淄博]25的平方根是 ⁠.
4. [母题·教材P62习题A组T2]下列说法正确的是(　A　)