



冀教版八年级上册17.3 勾股定理集体备课课件ppt
展开1. 会运用勾股定理解决简单的实际问题.2. 学会选择适当的数学模型解决实际问题.3. 能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
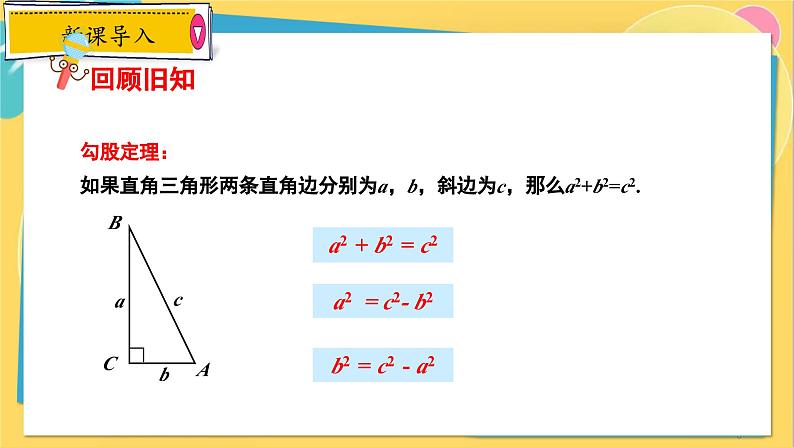
勾股定理:如果直角三角形两条直角边分别为a,b,斜边为c,那么a2+b2=c2.
a2 + b2 = c2
a2 = c2- b2
b2 = c2 - a2
历史上伦敦克里斯蒂拍卖行贴出了一个土地拍卖广告:如图所示,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能计算出池塘的准确面积,则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗?
勾股定理能解决直角三角形的许多问题,因此在现实生活中有着广泛的应用.
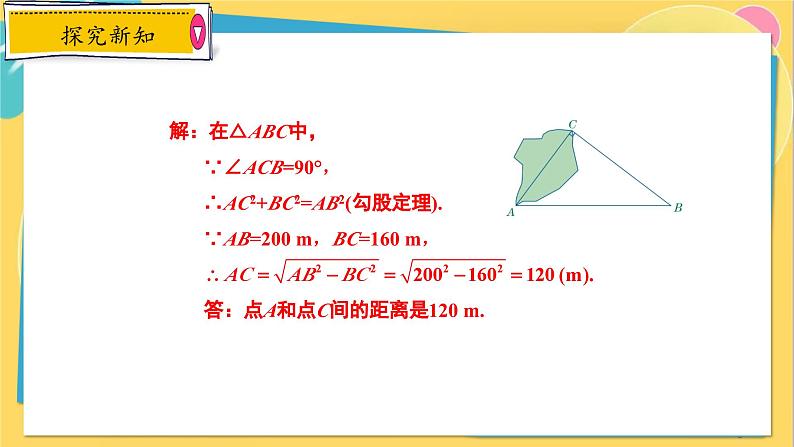
如图,为了测得湖边上点A和点C间的距离,一观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200 m,BC=160 m. 根据测量结果,求点A和点C间的距离.
基本思想方法:勾股定理把“形”与“数”有机地结合起来,即把直角三角形这个“形”与三边关系这一“数”结合起来,它是数形结合思想的典范.
解:在△ABC中, ∵∠ACB=90°, ∴AC2+BC2=AB2(勾股定理). ∵AB=200 m,BC=160 m, 答:点A和点C间的距离是120 m.
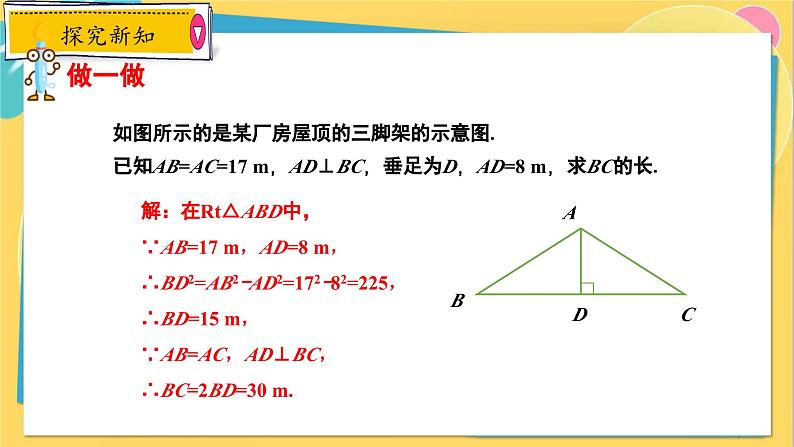
如图所示的是某厂房屋顶的三脚架的示意图. 已知AB=AC=17 m,AD⊥BC,垂足为D,AD=8 m,求BC的长.
解:在Rt△ABD中,∵AB=17 m,AD=8 m,∴BD2=AB2-AD2=172-82=225,∴BD=15 m,∵AB=AC,AD⊥BC,∴BC=2BD=30 m.
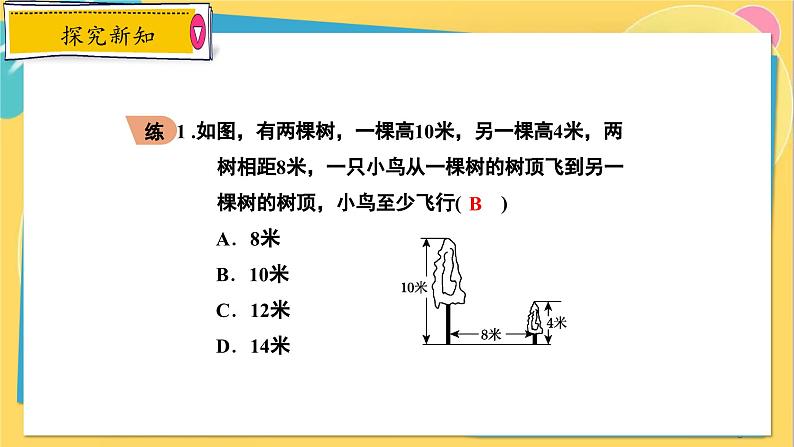
1 .如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( ) A.8米 B.10米 C.12米 D.14米
2.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1.5 m处折断,树尖B恰好碰到地面,经测量AB=2 m,则树高为 m.
解决这类实际问题的关键是根据题意,画出图形,建立数学模型,用数学知识解答,把复杂问题简单化、明朗化.
点拨:利用勾股定理求未知边长时,关键要找准斜边,找斜边,就是找直角,直角所对的边就是斜边.
如图,在长为50 mm,宽为40 mm的长方形零件上有两个圆孔,与孔中心A,B相关的数据如图所示.求孔中心A和B间的距离.
解:∵△ABC是直角三角形, ∴ AB2=AC2+BC2. ∵AC=50-15-26=9(mm), BC=40-18-10=12(mm), 答:孔中心A和B间的距离是15 mm.
1.如图所示,水池中有水,水面是一个边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边,那么它的顶端恰好到达池边的水面.水的深度和这根芦苇的长度分别是多少?
解:设水深为x尺,则芦苇长度为(x+1)尺,根据勾股定理得x2+ =(x+1)2,解得x=12,x+1=12+1=13.答:水深为12尺,芦苇的长度为13尺.
2.如图,在△ABC中,AB=AC=12,BC=16. 求△ABC的面积.
解:过点A作AD⊥BC,交BC于点D. ∵AB=AC,∴AD是△ABC底边BC上的中线, ∴BD=CD= BC= ×16=8. 在Rt△ABD中,由勾股定理, 得AD2=AB2-BD2=122-82=80,AD= . ∴S△ABC = BC·AD= ×16× = .
勾股定理的实际应用的一般步骤:
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12 cm,高是20 cm,那么所需彩带最短的是多少?
分析:要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.
解: 由图可知,彩带从易拉罐底端的 A处绕易拉罐 4 圈后到达顶端的B处,将易拉罐表面切开展开呈 长方形,则螺旋线长为四个长方形并排后的长方 形的对角线长,设彩带最短长度为x,则易拉罐底 面周长是12 cm,高是20 cm, ∴x2=202+(12×4)2, 解得:x=52 所以彩带最短是52 cm.
本题考查了平面展开——最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开呈矩形,“化曲面为平面”,用勾股定理解决.
1.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为________.
2.如图所示,一圆柱高8 cm,底面半径为2 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( ) A. 20 cm B. 10 cm C. 14 cm D.无法确定
2. [母题·教材P15习题T5]《九章算术》中有一道“引葭赴 岸”问题:今有池一丈,葭生其中央,出水一尺,引葭赴 岸,适与岸齐,问水深、葭长各几何?题意是:有一个池 塘,其池面是边长为10尺的正方形,一棵芦苇 AC 生长在 它的中央,高出水面部分 BC 为1尺,如果把该芦苇沿与 水池边垂直的方向拉向岸边,那么芦苇的顶部 C 恰好碰到 岸边的C'处(如图),问水深和芦苇长各多少尺?则该问题 中的水深是 尺.
3. [2023·广安]如图,圆柱形玻璃杯的杯高为9 cm,底面周长 为16 cm,在杯内壁离杯底4 cm的点 A 处有一滴蜂蜜,此 时,一只蚂蚁正好在杯外壁上,它在离杯上沿1 cm,且与 蜂蜜相对的点 B 处,则蚂蚁从外壁 B 处到内壁 A 处所走的 最短路程为 cm.(杯壁厚度不计)
初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理评课课件ppt: 这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理评课课件ppt,文件包含SectionBpptx、SectionA-1ppt、SectionA-2pptx、SelfCheckppt、SectionA1bmp3、SectionA2amp3、SectionA2bmp3、SectionA2dmp3、SectionB1cmp3、SectionB1dmp3、SectionB2bmp3、wordsandexpressionsUnit2mp3等12份课件配套教学资源,其中PPT共143页, 欢迎下载使用。
初中数学北师大版八年级上册第一章 勾股定理3 勾股定理的应用课文配套ppt课件: 这是一份初中数学北师大版八年级上册第一章 勾股定理3 勾股定理的应用课文配套ppt课件,共16页。PPT课件主要包含了回顾与思考,问题的提出,问题的延伸,做一做,试一试,算一算,x24,知识小结,作业见作业本2,补充练习等内容,欢迎下载使用。
人教版八年级下册第十七章 勾股定理17.1 勾股定理示范课ppt课件: 这是一份人教版八年级下册第十七章 勾股定理17.1 勾股定理示范课ppt课件,共19页。PPT课件主要包含了教学目标,复习回顾,什么是勾股定理,问题1,几何语言,新知探究,探究一,问题2,探究二,∴OB1等内容,欢迎下载使用。













