天一实验学校八年级下第一次月考数学试卷含答案解析

这是一份天一实验学校八年级下第一次月考数学试卷含答案解析，共20页。试卷主要包含了若式子有意义，则x的取值范围是，若反比例函数y=，下列计算正确的是，如图，点P是反比例函数y=，在函数y=等内容，欢迎下载使用。
一．选择题：（本大题共10小题，每题3分，共30分.）
1．若式子有意义，则x的取值范围是（ ）
A．x≥3 B．x≤3 C．x＞3 D．x=3
2．下列函数中，y是x的反比例函数有（ ）
（1）y=3x；（2）y=﹣；（3）；（4）﹣xy=3；（5）；（6）；（7）y=2x；（8）．
A．（2）（4） B．（2）（3）（5）（8） C．（2）（7）（8） D．（1）（3）（4）（6）
3．若反比例函数y=（k≠0）的图象经过点（﹣2，3），则k的值是（ ）
A．﹣B．﹣C．6 D．﹣6
4．下列计算正确的是（ ）
A．=﹣4 B．（）=4 C．+=D．÷=3
5．一元二次方程3x﹣2x=1的二次项系数、一次项系数、常数项分别是（ ）
A．3，2，1 B．3，2，1 C．3，﹣2，﹣1 D．﹣3，2，1
6．关于反比例函数y=﹣，下列说法正确的是（ ）
A．图象过（1，2）点 B．图象在第一、三象限
C．当x＞0时，y随x的增大而减小 D．当x＜0时，y随x的增大而增大
7．如图，点P是反比例函数y=（x＞0）的图象上的任意一点，过点P分别作两坐标轴的垂线，与坐标轴构成矩形OAPB，点D是矩形OAPB内任意一点，连接DA、DB、DP、DO，则图中阴影部分的面积是（ ）
A．1 B．2 C．3 D．4．
8．已知x关于的一次函数y=mx+n的图象如上图，则|n﹣m|﹣可化简（ ）
A．n B．n﹣2m C．m D．2n﹣m
9．在函数y=（k为常数）的图象上有三个点（x，﹣2），（x，﹣1），（x，3），则x，x，x的大小关系为（ ）
A．x＜x＜xB．x＜x＜xC．x＜x＜xD．x＜x＜x
10．对于两个已知图形G、G，在G上任取一点P，在G上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G、G的“密距”．例如，如上图，A（﹣2，3），B（1，3），C（1，0），则点A与射线OC之间的“密距”为，点B与射线OC之间的“密距”为3．如果直线y=x﹣1和双曲线y=之间的“密距”为，则k值为（ ）
A．k=4 B．k=﹣4 C．k=6 D．k=﹣6

二．填空题：（本大题共8小题，每空2分，共18分.）
11．已知y=（m+1）是反比例函数，则m= ．
12．写出的一个同类二次根式 ；把（a﹣2）根号外的因式移到根号内后，其结果是 ．
13．实数x、y满足y=﹣+2，则x﹣y= ．
14．若关于x的一元二次方程x2﹣2x+m=0有实数根，则m的最大整数值为 ．
15．已知在同一坐标系中，某正比例函数与某反比例函数的图象交于A，B两点，若点A的坐标为（﹣1，4），则点B的坐标为 ．
16．已知函数y1=x（x＞0），y2=（x＞0）的图象如图，有下列结论：
①两函数图象的交点A的坐标为（3，3）；
②当x＞3时，y2＞y1；
③BC=4；
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确的结论有 ．
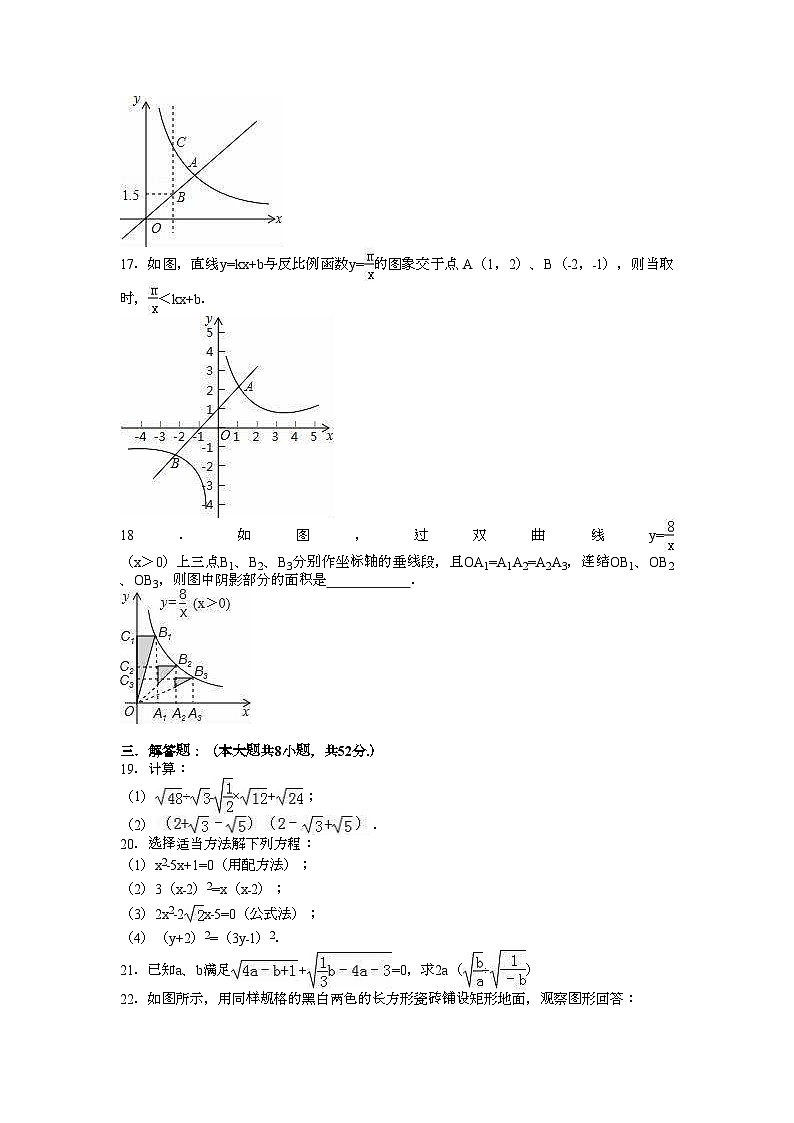
17．如图，直线y=kx+b与反比例函数y=的图象交于点 A（1，2）、B（﹣2，﹣1），则当取 时，＜kx+b．
18．如图，过双曲线y=（x＞0）上三点B1、B2、B3分别作坐标轴的垂线段，且OA1=A1A2=A2A3，连结OB1、OB2、OB3，则图中阴影部分的面积是 ．

三．解答题：（本大题共8小题，共52分.）
19．计算：
（1）÷﹣×+；
（2）．
20．选择适当方法解下列方程：
（1）x2﹣5x+1=0（用配方法）；
（2）3（x﹣2）2=x（x﹣2）；
（3）2x2﹣2x﹣5=0（公式法）；
（4）（y+2）2=（3y﹣1）2．
21．已知a、b满足+=0，求2a（÷）
22．如图所示，用同样规格的黑白两色的长方形瓷砖铺设矩形地面，观察图形回答：
（1）第n个图形中每一横行共有 块瓷砖，每一竖列共有 块瓷砖（用含n的代数式表示）；
（2）设铺设地面所用瓷砖总块数为y，请写出用n表示y的关系式；
（3）按上述铺设方案，铺一块这样的矩形地面只需506块砖，求此时的n的值．
23．如图，一次函数 y1=kx+2的图象与反比例函数y2=﹣（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且BC=2AB．
（1）求一次函数的解析式，并直接写出使得y1≤y2的x的取值范围；
（2）设函数y3=（x＞0）的图象与y2=﹣（x＜0）的图象关于y轴对称，在y3=（x＞0）的图象上取一点P（P点的横坐标大于2），过P作PQ⊥x轴，垂足为Q，若四边形BCQP的面积等于2，求P点的坐标．
24．阅读下列材料，然后回答问题．在进行二次根式的化简与运算时，我们有时会碰上如，，一样的式子，其实我们还可以将其进一步化简：
==；（一）
==（二）
===﹣1（三）
以上这种化简的步骤叫做分母有理化．
化简：．
25．我们知道，一次函数y=x+1的图象可以由正比例函数y=x的图象向左平移1个单位得到；爱动脑的小聪认为：函数y=也可以由反比例函数y=通过平移得到，小明通过研究发现，事实确实如此，并指出了平移规律，即只要把y=（双曲线）的图象向左平移1个单位（如图1虚线所示），同时函数y=的图象上下都无限逼近直线x=﹣1．
如图2，已知反比例函C：y=与正比例函数L：y=k2x的图象相交于点A（1，2）和点B．
（1）写出点B的坐标，并求k1和k2的值；
（2）将函数y=的图象C与直线L同时向右平移n（n＞0）个单位长度，得到的图象分别记为C′和L′，已知图象L′经过点M（3，2）；
则①n的值为；②写出平移后的图象C′对应的函数关系式为 ；
③利用图象，直接写出不等式＞2x﹣4的解集为 ．
26．已知点P（a，b）是反比例函数y=﹣（x＜0）图象上的动点，PA∥x轴，PB∥y轴，分别交反比例函数y=﹣（x＜0）的图象于点A，B，交坐标轴于C，D．
（1）记△POD的面积为S1，△BOD的面积为S2，直接写出S1：S2= （求比值）
（2）请用含a的代数式分别表示P，A，B三点的坐标；
（3）在点P运动过程中，连接AB，设△PAB的面积为S，则S是否变化？若不变化，请求出S的值；若改变，请写出S关于a的函数关系式．

2022-2023江苏省无锡市天一实验学校八年级（下）第一次月考数学试卷
参考答案与试题解析

一．选择题：（本大题共10小题，每题3分，共30分.）
1．若式子有意义，则x的取值范围是（ ）
A．x≥3 B．x≤3 C．x＞3 D．x=3
【考点】二次根式有意义的条件．
【分析】根据二次根式有意义的条件即可求解．
【解答】解：根据题意得：x﹣3≥0，
解得：x≥3．
故选：A．

2．下列函数中，y是x的反比例函数有（ ）
（1）y=3x；（2）y=﹣；（3）；（4）﹣xy=3；（5）；（6）；（7）y=2x﹣2；（8）．
A．（2）（4） B．（2）（3）（5）（8） C．（2）（7）（8） D．（1）（3）（4）（6）
【考点】反比例函数的定义．
【分析】分别利用正比例函数以及反比例函数的定义分析得出答案．
【解答】解：（1）y=3x，是正比例函数，故此选项错误；
（2）y=﹣，是反比例函数，故此选项正确；
（3）是正比例函数，故此选项错误；
（4）﹣xy=3是反比例函数，故此选项正确；
（5），y是x+1的反比例函数，故此选项错误；
（6），y是x2的反比例函数，故此选项错误；
（7）y=2x﹣2，y是x2的反比例函数，故此选项错误；
（8），k≠0时，y是x的反比例函数，故此选项错误．
故选：A．

3．若反比例函数y=（k≠0）的图象经过点（﹣2，3），则k的值是（ ）
A．﹣B．﹣C．6 D．﹣6
【考点】反比例函数图象上点的坐标特征．
【分析】直接根据反比例函数图象上点的坐标特征求解．
【解答】解：∵反比例函数y=（k≠0）的图象经过点（﹣2，3），
∴k=﹣2×3=﹣6．
故选D．

4．下列计算正确的是（ ）
A．=﹣4 B．（）2=4 C．+=D．÷=3
【考点】二次根式的混合运算．
【分析】根据二次根式的性质对A、B进行判断；根据二次根式的加减法对C进行判断；根据二次根式的除法法则对D进行判断．
【解答】解：A、原式=|﹣4|=4，所以A选项错误；
B、原式=2，所以B选项错误；
C、与不能合并，所以C选项错误；
D、原式==3，所以D选项正确．
故选D．

5．一元二次方程3x2﹣2x=1的二次项系数、一次项系数、常数项分别是（ ）
A．3，2，1 B．3，2，1 C．3，﹣2，﹣1 D．﹣3，2，1
【考点】一元二次方程的一般形式．
【分析】要确定二次项系数、一次项系数和常数项，首先要把方程化成一般形式．
【解答】解：∵方程3x2﹣2x=1化成一般形式是3x2﹣2x﹣1=0，
∴二次项系数是3，一次项系数为﹣2，常数项为﹣1．
故选：C．

6．关于反比例函数y=﹣，下列说法正确的是（ ）
A．图象过（1，2）点 B．图象在第一、三象限
C．当x＞0时，y随x的增大而减小 D．当x＜0时，y随x的增大而增大
【考点】反比例函数的性质．
【分析】反比例函数y=（k≠0）的图象k＞0时位于第一、三象限，在每个象限内，y随x的增大而减小；k＜0时位于第二、四象限，在每个象限内，y随x的增大而增大；在不同象限内，y随x的增大而增大，根据这个性质选择则可．
【解答】解：∵k=﹣2＜0，所以函数图象位于二四象限，在每一象限内y随x的增大而增大，图象是轴对称图象，故A、B、C错误．
故选D．

7．如图，点P是反比例函数y=（x＞0）的图象上的任意一点，过点P分别作两坐标轴的垂线，与坐标轴构成矩形OAPB，点D是矩形OAPB内任意一点，连接DA、DB、DP、DO，则图中阴影部分的面积是（ ）
A．1 B．2 C．3 D．4．
【考点】反比例函数系数k的几何意义．
【分析】首先根据反比例系数k的几何意义，可知矩形OAPB的面积=6，然后根据题意，得出图中阴影部分的面积是矩形OAPB的面积的一半，从而求出结果．
【解答】解：∵P是反比例函数的图象的任意点，过点P分别做两坐标轴的垂线，
∴与坐标轴构成矩形OAPB的面积=6．
∴阴影部分的面积=×矩形OAPB的面积=3．
故选C．

8．已知x关于的一次函数y=mx+n的图象如上图，则|n﹣m|﹣可化简（ ）
A．n B．n﹣2m C．m D．2n﹣m
【考点】一次函数图象与系数的关系．
【分析】根据一次函数图象与系数的关系，确定m、n的符号，然后由绝对值、二次根式的化简运算法则解得即可．
【解答】解：根据图示知，关于x的一次函数y=mx+n的图象经过第一、二、四象限，
∴m＜0，n＞0；
∴|n﹣m|﹣
=n﹣m﹣（﹣m）+（n﹣m）
=2n﹣m．
故选D．

9．在函数y=（k为常数）的图象上有三个点（x1，﹣2），（x2，﹣1），（x3，3），则x1，x2，x3的大小关系为（ ）
A．x1＜x2＜x3B．x3＜x1＜x2C．x3＜x2＜x1D．x2＜x1＜x3
【考点】反比例函数图象上点的坐标特征．
【分析】先根据反比例的解析式判断出函数图象所在的象限及增减性，再根据各点横坐标的特点即可得出结论．
【解答】解：∵y=（k为常数）中﹣k2﹣1＜0，
∴函数图象的两个分式分别位于二、四象限，且在每一象限内y随x的增大而增大．
∵﹣2＜0，﹣1＜0，
∴点（x1，﹣2），（x2，﹣1）位于第四象限，
∴x1＞0，x2＞0，
∵﹣2＜﹣1＜0，
∴0＜x1＜x2．
∵3＞0，
∴点（x3，3）位于第二象限，
∴x3＜0，
∴x3＜x1＜x2．
故选B．

10．对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1、G2的“密距”．例如，如上图，A（﹣2，3），B（1，3），C（1，0），则点A与射线OC之间的“密距”为，点B与射线OC之间的“密距”为3．如果直线y=x﹣1和双曲线y=之间的“密距”为，则k值为（ ）
A．k=4 B．k=﹣4 C．k=6 D．k=﹣6
【考点】反比例函数与一次函数的交点问题．
【分析】由题意设双曲线上的D到直线的距离最近，过D作直线l和直线y=x﹣1的平行线，结合条件可求得l的解析式，联立l与双曲线解析式，则该方程组只有一组解，可求得k的值．
【解答】解：
根据“密距”的定义可知双曲线图象在二、四象限，且离第四象限最近，
设双曲线上点D到直线y=x﹣1距离最近，如图，设直线y=x﹣1与y轴交于点E，过D作直线y=x﹣1的平行线，交y轴于点G，过D作直线y=x﹣1的垂线，垂足为E，过E作EH⊥DG，垂足为H，
则由题意可知DF=EH=，
又∠OEF=45°，
∴∠EGH=45°，
∴EH=HG=，
∴EG=EH=×=3，
又OE=1，
∴OG=4，
∴直线DG的解析式为y=x﹣4，
联立直线DG和双曲线解析式可得，消去y整理可得x2﹣4x﹣k=0，
∵直线DG与双曲线只有一个交点，
∴方程x2﹣4x﹣k=0有两个相等的实数根，
∴△=0，即（﹣4）2+4k=0，解得k=﹣4，
故选B．

二．填空题：（本大题共8小题，每空2分，共18分.）
11．已知y=（m+1）是反比例函数，则m= 1 ．
【考点】反比例函数的定义．
【分析】根据反比例函数的定义．即y=（k≠0），只需令m2﹣2=﹣1、m+1≠0即可．
【解答】解：∵y=（m+1）是反比例函数，
∴，
解之得m=1．
故答案为：1．

12．写出的一个同类二次根式 3 ；把（a﹣2）根号外的因式移到根号内后，其结果是 ﹣ ．
【考点】同类二次根式；二次根式的性质与化简．
【分析】先将化简为最简二次根式，然后根据同类项二次根式的定义回答即可；先确定出2﹣a的正负，然后再进行变形即可．
【解答】解：=2，的一个同类二次根式可以是3；
∵被开方数等于0．分母不为0，
∴2﹣a＞0．
∴a﹣2＜0．
∴原式=﹣（2﹣a）=﹣=﹣．
故答案为：3（答案不唯一）；﹣．

13．实数x、y满足y=﹣+2，则x﹣y= ﹣1 ．
【考点】二次根式有意义的条件．
【分析】根据二次根式有意义的条件可得x﹣1≥0，1﹣x≥0，从而可确定x的值为1，进而可得y的值，然后再计算出x﹣y即可．
【解答】解：由题意得：x﹣1≥0，1﹣x≥0，
解得x=1，
则y=2，
x﹣y=﹣1，
故答案为：﹣1．

14．若关于x的一元二次方程x2﹣2x+m=0有实数根，则m的最大整数值为 1 ．
【考点】根的判别式．
【分析】方程有实数根即△≥0，根据△建立关于m的不等式，求m的取值范围，进一步确定m的最大整数值．
【解答】解：由题意知，△=4﹣4m≥0，
∴m≤1
m的最大整数值是1．
故答案为：1．

15．已知在同一坐标系中，某正比例函数与某反比例函数的图象交于A，B两点，若点A的坐标为（﹣1，4），则点B的坐标为 （1，﹣4） ．
【考点】反比例函数图象的对称性．
【分析】根据反比例函数图象上点的坐标特征，正比例函数与反比例函数的两交点坐标关于原点对称．
【解答】解：∵反比例函数是中心对称图形，正比例函数与反比例函数的图象的两个交点关于原点对称，
∵一个交点的坐标为（﹣1，4），
∴它的另一个交点的坐标是（1，﹣4），
故答案为：（1，﹣4）．

16．已知函数y1=x（x＞0），y2=（x＞0）的图象如图，有下列结论：
①两函数图象的交点A的坐标为（3，3）；
②当x＞3时，y2＞y1；
③BC=4；
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确的结论有 ①④ ．
【考点】反比例函数与一次函数的交点问题．
【分析】根据题意可以求得两函数图象的交点A的坐标，从而可以判断①；根据点A的坐标可以判断②；根据点B的纵坐标可以分别求出点B、C的坐标，从而可以得到BC的值，从而可以判断③；根据函数图象可以判断④．
【解答】解：由题意可得，
（x＞0）
解得，x=3，
将x=3代入y1=x，得y1=3，
∴两函数图象的交点A的坐标为（3，3），故①正确；
由图象可知，当x＞3时，y1＞y2，故②错误；
将y=1.5代入y1=x得，x=1.5，
将x=1.5代入y2=得，y2=6，
∴BC=6﹣1.5=4.5，故③错误；
由图象可知，当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小，故④正确；
故答案为：①④．

17．如图，直线y=kx+b与反比例函数y=的图象交于点 A（1，2）、B（﹣2，﹣1），则当取 ﹣2＜x＜0或x＞1 时，＜kx+b．
【考点】反比例函数与一次函数的交点问题．
【分析】根据函数图象可以明确x＜﹣2，﹣2＜x＜0，0＜x＜1，x＞1时直线y=kx+b与反比例函数y=对应的函数值的大小，从而可以解答本题．
【解答】解：由图象可知，当x＜﹣2时，＞kx+b，
当﹣2＜x＜0时，＜kx+b，
当0＜x＜1时，＞kx+b，
当x＞1时，＜kx+b．
故答案为：﹣2＜x＜0或x＞1．

18．如图，过双曲线y=（x＞0）上三点B1、B2、B3分别作坐标轴的垂线段，且OA1=A1A2=A2A3，连结OB1、OB2、OB3，则图中阴影部分的面积是 ．
【考点】反比例函数系数k的几何意义．
【分析】先根据反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值得到S△OB1C1=S△OB2C2=S△OB3C3=k=4，再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和．
【解答】解：根据题意可知S△OB1C1=S△OB2C2=S△OB3C3=k=4
∵OA1=A1A2=A2A3，A1B1∥A2B2∥A3B3∥y轴
设图中阴影部分的面积从左向右依次为s1，s2，s3
则s1=k=4，
∵OA1=A1A2=A2A3，
∴s2：S△OB2C2=1：4，s3：S△OB3C3=1：9
∴图中阴影部分的面积分别是s1=4，s2=1，s3=
∴图中阴影部分的面积之和=4+1+=．
故答案为：．

三．解答题：（本大题共8小题，共52分.）
19．计算：
（1）÷﹣×+；
（2）．
【考点】二次根式的混合运算．
【分析】（1）先进行二次根式的乘除运算，然后化简后合并即可；
（2）先变形得到原式=[2+（3﹣）][2﹣（3﹣）]，然后利用平方差公式和完全平方公式计算即可．
【解答】解：（1）原式=﹣+2
=4﹣+2
=4+；
（2）原式=[2+（3﹣）][2﹣（3﹣）]
=22﹣（3﹣）2
=4﹣（9﹣6+5）
=4﹣14+6
=﹣10+6．

20．选择适当方法解下列方程：
（1）x2﹣5x+1=0（用配方法）；
（2）3（x﹣2）2=x（x﹣2）；
（3）2x2﹣2x﹣5=0（公式法）；
（4）（y+2）2=（3y﹣1）2．
【考点】解一元二次方程-因式分解法；解一元二次方程-配方法；解一元二次方程-公式法．
【分析】（1）利用配方法得到（x﹣）2=，然后根据直接开平方法求解；
（2）先变形得到3（x﹣2）2﹣x（x﹣2）=0，然后利用因式分解法解方程；
（3）先计算判别式的值，然后利用求根公式法求解；
（4）先变形得到（y+2）2﹣（3y﹣1）2=0，然后利用因式分解法解方程．
【解答】解：（1）x2﹣5x=﹣1，
x2﹣5x+（）2=﹣1+（）2，
（x﹣）2=，
x﹣=±，
所以x1=，x2=；
（2）3（x﹣2）2﹣x（x﹣2）=0，
（x﹣2）（3x﹣6﹣x）=0，
所以x1=2，x2=3；
（3）△=（﹣2）2﹣4×2×（﹣5）=48
x===，
所以x1=，x2=；
（4）（y+2）2﹣（3y﹣1）2=0，
（y+2+3y﹣1）（y+2﹣3y+1）=0，
y+2+3y﹣1=0或y+2﹣3y+1=0，
所以y1=﹣，y2=．

21．已知a、b满足+=0，求2a（÷）
【考点】二次根式的化简求值；非负数的性质：算术平方根．
【分析】根据非负数性质可得关于a、b的方程组，求得a、b的值代入计算即可．
【解答】解：根据题意，得：，
解得：，
故2a（÷）
=2×（﹣1）×（÷）
=﹣2×（×）
=﹣2×3
=﹣6．

22．如图所示，用同样规格的黑白两色的长方形瓷砖铺设矩形地面，观察图形回答：
（1）第n个图形中每一横行共有 n+3 块瓷砖，每一竖列共有 n+2 块瓷砖（用含n的代数式表示）；
（2）设铺设地面所用瓷砖总块数为y，请写出用n表示y的关系式；
（3）按上述铺设方案，铺一块这样的矩形地面只需506块砖，求此时的n的值．
【考点】一元二次方程的应用；规律型：图形的变化类．
【分析】（1）根据每行瓷砖数量得出规律，即可得出答案；
（2）找出瓷砖每行与每列与图形数之间的规律，即可解答；
（3）利用因式分解法解一元二次方程求出即可．
【解答】解：（1）（n+3），（n+2）；
（2）y=（n+3）（n+2）=n2+5n+6；
（3）当y=506时，
n2+5n+6=506，
n2+5n﹣500=0，
（n﹣20）（n+25）=0，
解得：n=20或n=﹣25（舍去）．
答：此时n为20．

23．如图，一次函数 y1=kx+2的图象与反比例函数y2=﹣（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且BC=2AB．
（1）求一次函数的解析式，并直接写出使得y1≤y2的x的取值范围；
（2）设函数y3=（x＞0）的图象与y2=﹣（x＜0）的图象关于y轴对称，在y3=（x＞0）的图象上取一点P（P点的横坐标大于2），过P作PQ⊥x轴，垂足为Q，若四边形BCQP的面积等于2，求P点的坐标．
【考点】反比例函数与一次函数的交点问题．
【分析】（1）在一次函数中令y=0可求得x=2，可求得B点坐标，过A作AH⊥x轴于H，由条件可求得A点坐标，代入一次函数解析式可求得k的值，可求得一次函数解析式，结合图象可求得y1≤y2的x的取值范围；
（2）由对称性可求得y3=的解析式，设P点坐标为（m，n），连接OP，利用四边形BCQP的面积可求得m的值，可求得P点坐标．
【解答】解：（1）在y1=kx+2中，令x=0，可求得y1=2，
∴B（0，2），
如图1，作AH⊥x轴于H，
∵BC=2AB，
∴AC=BC，
∴AH=OB=3，
∴A（﹣1，3），
代入y1=kx+2，可得3=﹣k+2，解得k=﹣1，
∴一次函数解析式为y1=﹣x+2，
∵A点坐标为（﹣1，3），
∴当﹣1≤x＜0时，y1≤y2；
（2）∵y3=（x＞0）的图象与y2=﹣（x＜0）的图象关于y轴对称，
∴y3=（x＞0），
设P（m，n），其中m＞2，如图2，连接OP，
则S四边形BOQP=S△BOP+S△POQ=S△BOC+S四边形BCQP，
即×2×m+×3=×2×2+2，解得m=，
∴P（，）．

24．阅读下列材料，然后回答问题．在进行二次根式的化简与运算时，我们有时会碰上如，，一样的式子，其实我们还可以将其进一步化简：
==；（一）
==（二）
===﹣1（三）
以上这种化简的步骤叫做分母有理化．
化简：．
【考点】分母有理化．
【分析】原式各项分母有理化，计算即可得到结果．
【解答】解：原式=++…+
=（﹣1+﹣+…+﹣）
=（﹣1）．

25．我们知道，一次函数y=x+1的图象可以由正比例函数y=x的图象向左平移1个单位得到；爱动脑的小聪认为：函数y=也可以由反比例函数y=通过平移得到，小明通过研究发现，事实确实如此，并指出了平移规律，即只要把y=（双曲线）的图象向左平移1个单位（如图1虚线所示），同时函数y=的图象上下都无限逼近直线x=﹣1．
如图2，已知反比例函C：y=与正比例函数L：y=k2x的图象相交于点A（1，2）和点B．
（1）写出点B的坐标，并求k1和k2的值；
（2）将函数y=的图象C与直线L同时向右平移n（n＞0）个单位长度，得到的图象分别记为C′和L′，已知图象L′经过点M（3，2）；
则①n的值为；②写出平移后的图象C′对应的函数关系式为 y= ；
③利用图象，直接写出不等式＞2x﹣4的解集为 x＜1或2＜x＜3 ．
【考点】反比例函数综合题．
【分析】（1）由反比例函数的对称性根据A的坐标求出B的坐标，把A坐标代入反比例解析式求出k1的值，代入正比例解析式求出k2的值即可；
（2）①利用平移规律表示出直线L′解析式，把M坐标代入求出n的值即可；②把n的值代入即可确定出C′解析式；③画出两函数图象，找出反比例函数图象位于一次函数图象上方时x的范围即可．
【解答】解：（1）由对称性得到B（﹣1，﹣2），
把A（1，2）代入反比例解析式得：k1=2，代入正比例解析式得：k2=2；
（2）①直线L向右平移n个单位，得到y=2（x﹣n），
把M（3，2）代入得：2=2（3﹣n），即n=2；
②平移后的图象C′对应的函数关系式为y=；
③如图所示，由平移规律得：A′（3，2），B′（1，﹣2），
则不等式＞2x﹣4的解集为x＜1或2＜x＜3，
故答案为：（2）②y=；③x＜1或2＜x＜3

26．已知点P（a，b）是反比例函数y=﹣（x＜0）图象上的动点，PA∥x轴，PB∥y轴，分别交反比例函数y=﹣（x＜0）的图象于点A，B，交坐标轴于C，D．
（1）记△POD的面积为S1，△BOD的面积为S2，直接写出S1：S2= 3 （求比值）
（2）请用含a的代数式分别表示P，A，B三点的坐标；
（3）在点P运动过程中，连接AB，设△PAB的面积为S，则S是否变化？若不变化，请求出S的值；若改变，请写出S关于a的函数关系式．
【考点】反比例函数综合题．
【分析】（1）利用点P的坐标可求出S：，S2的值，即可得出S1：S2；
（2）由P（a，b）是反比例函数y=﹣（x＜0）图象上的动点，可得P（a，﹣），再由点A、B在反比例函数y=﹣（x＜0）即可得出点A、B的坐标；
（3）由S=|AP|•|BP|=，即可得出S不变化．
【解答】解：（1）∵P（a，b）是反比例函数y=﹣（x＜0）图象上的动点，
∵P（a，﹣），
∴S1=•（﹣a）•（﹣）=3，
∵B（a，﹣），
∴S2=•（﹣a）•（﹣）=1，
∴S1：S2=3：1=3．
故答案为：3．
（2）∵P（a，b）是反比例函数y=﹣（x＜0）图象上的动点，
∵P（a，﹣），
∵点B在反比例函数y=﹣（x＜0）上且横坐标为a，
∴B（a，﹣），
∵点A在反比例函数y=﹣（x＜0）上且纵坐标为﹣，
∴A（，﹣），
（3）不变化．
∵P（a，﹣），B（a，﹣），A（，﹣），PA∥x轴，PB∥y轴，
∴S=|AP|•|BP|=×（﹣a）[（﹣）﹣（﹣）]=．

4月30日