2023-2024学年江西省稳派上进联考高一下学期7月期末调研测试数学试题（含答案）

这是一份2023-2024学年江西省稳派上进联考高一下学期7月期末调研测试数学试题（含答案），共10页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。
1.已知向量a=(1,2x)，b=(2,−8)，若a/​/b，则x=( )
A. 2B. −2C. 4D. −4
2.若复数z=1−i+2i2，则|z|=( )
A. 2B. 3C. 2D. 1
3.已知sin(π2−α)=13，则cs(π+α)=( )
A. −13B. 13C. −2 23D. 2 23
4.已知平面α/​/平面β，a，b是平面α，β外两条不同的直线，则下列结论错误的是( )
A. 若a/​/α，则a/​/βB. 若b⊥α，则b⊥β
C. 若a/​/α，b/​/β，则a/​/bD. 若a⊥α，b⊥β，则a/​/b
5.已知函数f(x)=sin(x+φ)+ 3cs(x+φ)是奇函数，则tanφ=( )
A. 33B. − 33C. 3D. − 3
6.已知函数f(x)=12tan(2x−φ)(|φ|<π2)的单调递增区间是(kπ2−π6,kπ2+π3)(k∈Z)，则φ=( )
A. π3B. π4C. π6D. π12
7.在△ABC中，内角A，B，C的对边分别为a，b，c，已知a=3，b=1，csC=−13，则边c上的高为( )
A. 62B. 63C. 32D. 33
8.已知函数f(x)=4cs2(ωx2−π6)−1(ω>0)，若对任意的实数t，f(x)在区间(t,t+2π3)上的值域均为[−1,3]，则ω的取值范围为( )
A. (0,2)B. (0,3)C. (2,+∞)D. (3,+∞)
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
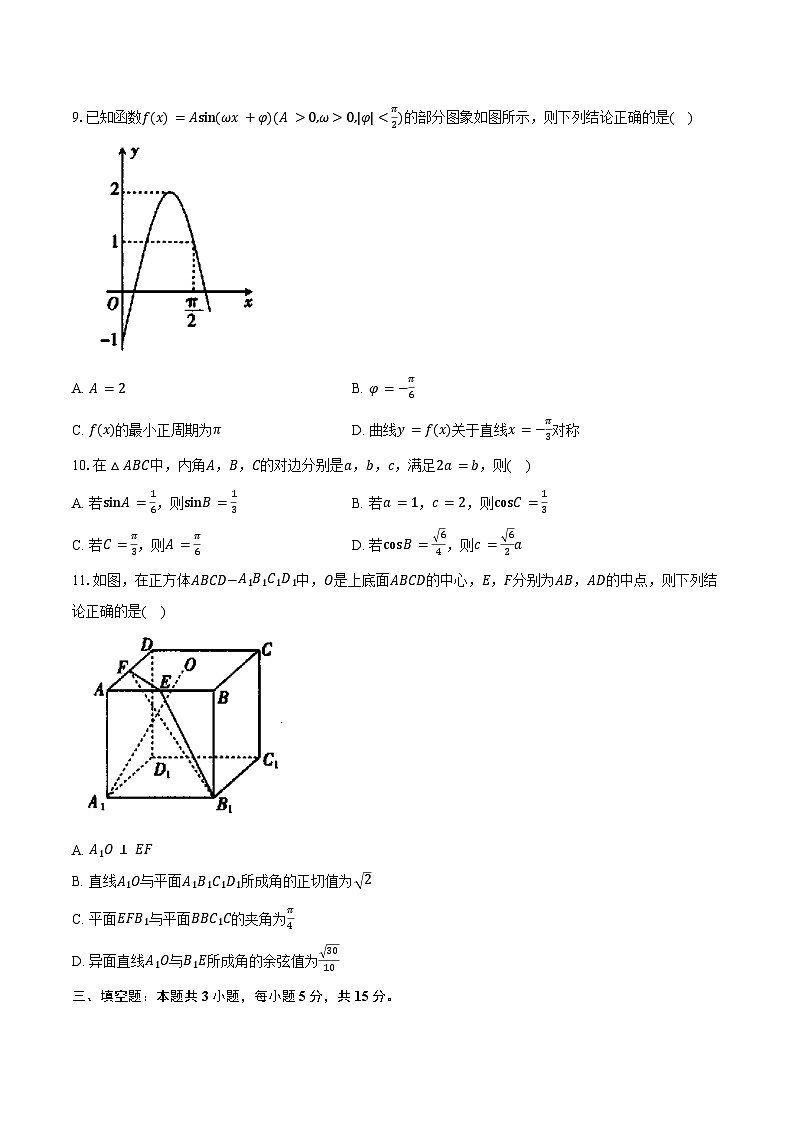
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示，则下列结论正确的是( )
A. A=2B. φ=−π6
C. f(x)的最小正周期为πD. 曲线y=f(x)关于直线x=−π3对称
10.在△ABC中，内角A，B，C的对边分别是a，b，c，满足2a=b，则( )
A. 若sinA=16，则sinB=13B. 若a=1，c=2，则csC=13
C. 若C=π3，则A=π6D. 若csB= 64，则c= 62a
11.如图，在正方体ABCD−A1B1C1D1中，O是上底面ABCD的中心，E，F分别为AB，AD的中点，则下列结论正确的是( )
A. A1O⊥EF
B. 直线A1O与平面A1B1C1D1所成角的正切值为 2
C. 平面EFB1与平面BBC1C的夹角为π4
D. 异面直线A1O与B1E所成角的余弦值为 3010
三、填空题：本题共3小题，每小题5分，共15分。
12.已知复数z=(2a−1)+ai(a∈R)在复平面内对应的点位于第二象限，则a的取值范围是 ．
13.已知三棱台ABC−A1B1C1的体积为V，记上底面A1B1C1、下底面ABC的面积分别为S1，S2，若S1:S2=1:4，则三棱锥B−A1B1C1的体积为 V.
14.如图，在Rt△ABC中，C=π2，A=π3，AB=2，O为斜边AB的中点，点M，N分别在边AC，BC上(不包括端点)，∠MON=2π3，若OM⋅ON=−14，则∠BON= ．
四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题13分)
已知|a|=2，|b|=3，且a⋅b=−4．
(1)若(a+kb)⊥a，求k的值;
(2)求b与a+b夹角的余弦值．
16.(本小题15分)
在△ABC中，内角A，B，C的对边分别是a，b，c，已知acsB2=bsin2A．
(1)证明：csAsinB2=14;
(2)若b2+c2=a2+ 2bc，求csB.
17.(本小题15分)
如图，正方体ABCD−A1B1C1D1的棱长为2，G，H分别是棱BB1，CC1的中点，M是棱C1D1上的一点，点N在棱AB上，BN=12，HCE−GBF是三棱柱，B，C分别是线段AF，DE的中点．
(1)证明：直线GN⊥平面EFGH;
(2)若四棱锥M−EFGH的体积为 56，求D1M的长度．
18.(本小题17分)
如图，某公园里的摩天轮的旋转半径为45米，最高点距离地面100米，某游客在最低点的位置坐上摩天轮，此时摩天轮开始运行，运行一周的时间不低于20分钟，在运行到5分钟时，他距地面大约32.5米．
(1)摩天轮运行一周约需要多少分钟?
(2)该公园规定每次游玩摩天轮只能运行一周，则该游客距地面大约77.5米时，摩天轮运行的时间是多少分钟?
19.(本小题17分)
对于平面向量xi(i=1,2,⋯,m,m≥3且m∈N)，记，Sm=x1+x2+⋯+xm，若存在xp(p∈{1,2,⋯,m})，使得|xp|≥|Sm+kxp|，k∈Z，则称xp是的“k向量”．
(1)设xn=(n,l−n)，n∈N∗，若x3是的“−3向量”，求实数l的取值范围;
(2)若xn=(cs2nπ3,sin2nπ3)，n∈N∗，则Ω3i+1(i∈N∗)是否存在“1向量”?若存在，求出“1向量”;若不存在，请说明理由;
(3)已知x1，x2，x3均为的“−1向量”，其中x1=(csx,−5sinx)，x2=(2csx,sinx).设平面直角坐标系xOy中的点列P1，P2，⋯，Pt(t∈N∗,t≥3)满足P1P2=x3(P1与原点O重合)，且P2k与P2k+1(k∈N∗)关于点P1对称，P2k+1与P2k+2关于点P2对称.求|P99P100|的取值范围．
参考答案
1.B
2.C
3.A
4.C
5.D
6.C
7.B
8.D
9.ABC
10.AC
11.ABD
12.(0,12)
13.17
14.π6
15.解：(1)因为(a+kb)⊥a，所以(a+kb)⋅a=0，
即a2+ka⋅b=0，
因为|a|=2，a⋅b=−4，
所以22−4k=0，解得k=1．
(2)b⋅(a+b)=a⋅b+b2=−4+32=5，
|a+b|= a2+2a⋅b+b2= 4−8+9= 5，
所以cs=b⋅(a+b)|b|⋅|a+b|=53× 5= 53，
所以b与a+b的夹角的余弦值为 53．
16.(1)证明：由acsB2=bsin2A，得acsB2=2bsinAcsA，
由正弦定理，得sinAcsB2=2sinBsinAcsA，
因为sinA≠0，所以csB2=2sinBcsA，
由二倍角公式得csB2=4sinB2csB2csA，
因为csB2≠0，所以csAsinB2=14．
(2)解：由b2+c2=a2+ 2bc，
得b2+c2−a2= 2bc，
所以csA=b2+c2−a22bc= 2bc2bc= 22，
因为csAsinB2=14，
所以 22sinB2=14，得sinB2= 24，
所以csB=1−2sin2B2=1−2×( 24)2=34．
17.(1)证明：依题意，GN2=1+14=54，
GF2=22+12=5，FN=12+2=52，
所以FN2=GN2+GF2，
所以△NGF是直角三角形，GN⊥GF．
因为BC⊥平面A1B1BA，GN⊂平面A1B1BA，所以BC⊥GN，
因为G，H分别是棱BB1，CC1的中点，
所以BC/​/GH，则GN⊥GH，
因为GH∩GF=G，GH，GF⊂平面EFGH，
所以GN⊥平面EFGH．
(2)解：连接D1H，A1G，
因为D1D//HC，D1D=2HC=2，C为DE的中点，
所以D1，H，E共线，
同理A1，G，F共线．
易知平面C1D1DC⊥平面EFGH，过点M作MO⊥平面EFGH，
则垂足O在交线D1E上，
则四棱锥M−EFGH的体积V=13S矩形EFGH⋅MO=13×2× 5⋅MO= 56，得MO=14．
因为△D1MO∽△D1HC1，
所以D1M 5=141，得D1M= 54．

18.解：如图，设AC为地面，圆O为摩天轮，其旋转半径为45米，最高点距离地面100米，则摩天轮的最低点B距离地面10米，即AB=10，以AC所在直线为x轴，BO所在直线为y轴，建立平面直角坐标系，(3分)某人在最低点B的位置坐上摩天轮，设第t分钟时所在位置的高度为ℎ(t)，则ℎ(t)=45sin(ωt−π2)+55(ω>0)．
(1)当t=5时，ℎ(5)=45sin(5ω−π2)+55=32.5，整理得sin(5ω−π2)=−12，
所以5ω−π2=−π6或5ω−π2=7π6，由于摩天轮运行一周的时间不低于20分钟，所以5ω−π2=7π6，不符合实际情况，舍去，所以5ω−π2=−π6，得ω=π15，所以周期T=2πω=30，所以摩天轮运行一周约需要30分钟．
(2)由(1)知ℎ(t)=45sin(π15t−π2)+55，当该游客距地面大约77.5米时，
得ℎ(t)=45sin(π15t−π2)+55=77.5，即sin(π15t−π2)=12，
所以π15t−π2=π6或π15t−π2=5π6，得t=10或t=20．
所以当该游客距地面大约77.5米时，摩天轮运行了10分钟或20分钟．
19.解：(1)因为x3是的“−3向量”，所以|x3|≥S3−3x3=|x1+x2−2x3|.
因为x1+x2−2x3=1,l−1+2,l−2−23,l−3=−3,3，
所以 32+(l−3)2≥ (−3)2+32，即l2−6l⩾0，解得l ≤0或l ≥6，
因此实数l 的取值范围是(−∞,0]∪[6,+∞).
(2)因为xn=(cs2nπ3,sin2nπ3)，所以xn = cs2 2nπ3+sin22nπ3=1．
因为x3j+n=(cs2(3j+n)π3,sin2(3j+n)π3)=(cs2nπ3,sin2nπ3)=xn (j∈N)，所以Ω3i+1 中的向量依次以3为周期．
若存在“1向量”xp，只需|S3i+1+xp|≤1.
因为x1+x2+x3=0，
所以S3i+1=(x1+x2+x3)+(x4+x5+x6)+⋯+(x3i−2+x3i−1+x3i)+x3i+1=x3i+1=x1=(cs2π3,sin2π3)=(−12, 32)，
因此由|S3i+1+xp|≤1得 (−12+cs2pπ3)2+( 32+sin2pπ3)2≤1，即 2+2sin(2pπ3−π6)≤1，
即0≤2+2sin(2pπ3−π6)≤1，即−1≤sin(2pπ3−π6)≤−12，
所以当p=2，3，5，6，⋯，3i−1，3i(i∈N∗)时，符合要求，因此存在“1向量”，且“1向量”为x2，x3，x5，x6，⋯，x3i−1，x3i(i∈N∗).
(3)因为x1 为 的“−1向量”，所以|x1|≥|x2+x3|，即x12≥(x2+x3)2，即x12≥x22+x32+2x2⋅x3．
同理可得：x22≥x12+x32+2x1⋅x3，x32≥x12+x22+2x1⋅x2，
以上三式相加，整理得：0≥x12+x22+x32+2x1⋅x2+2x2⋅x3+2x1⋅x3，即(x1+x2+x3)2≤0，即x1+x2+x3⩽0，
因此x1+x2+x3=0．
因为x1=(csx,−5sinx)，x2=(2csx,sinx)，所以x3=−x1+x2=(−3csx,4sinx)．
设Pi(xi,yi).
因为P2k与P2k+1(k∈N∗)关于点P1对称，P2k+1与P2k+2关于点P2对称，
所以(x2k+1,y2k+1)=2(x1,y1)−(x2k,y2k)(x2k+2,y2k+2)=2(x2,y2)−(x2k+1,y2k+1)，因此(x2k+2,y2k+2)=2[(x2,y2)−(x1,y1)]+(x2k，y2k)，
所以(x2k+2,y2k+2)=2k[(x2,y2)−(x1,y1)]+(x2，y2)，(x2k+1,y2k+1)=2k[(x1,y1)−(x2,y2)]+(x2，y2)，
因此P2k+1P2k+2=(x2k+2−x2k+1,y2k+2−y2k+1)=4k[(x2,y2)−(x1,y1)]=4kP1P2．
因为P1P2=x3，所以P1P22=x32=−3csx2+4sinx2=9+7sin2x∈9,16，
当且仅当x=k1π+π2(k1∈Z)时，|P1P2|2=16；x=k2π(k2∈Z)时，|P1P2|2=9，因此|P1P2|∈[3,4]．
因为P99P100=P2×49+1P2×49+2=4×49P1P2，所以P99P100=4×49P1P2∈4×49×3,4×49×4=588,784，
即|P9P100|的取值范围是[588,784]．