高考数学一轮复习【考点题型归纳讲练】导学案（新高考专用）专题研究概率与统计的综合问题(原卷版+解析)

这是一份高考数学一轮复习【考点题型归纳讲练】导学案（新高考专用）专题研究概率与统计的综合问题(原卷版+解析)，共22页。
【例1】某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200千瓦时的部分按元/千瓦时收费，超过200千瓦时但不超过400千瓦时的部分按元/千瓦时收费，超过400千瓦时的部分按元/千瓦时收费.
(1)求某户居民的用电费用（单位：元）关于月用电量（单位：千瓦时）的函数解析式；
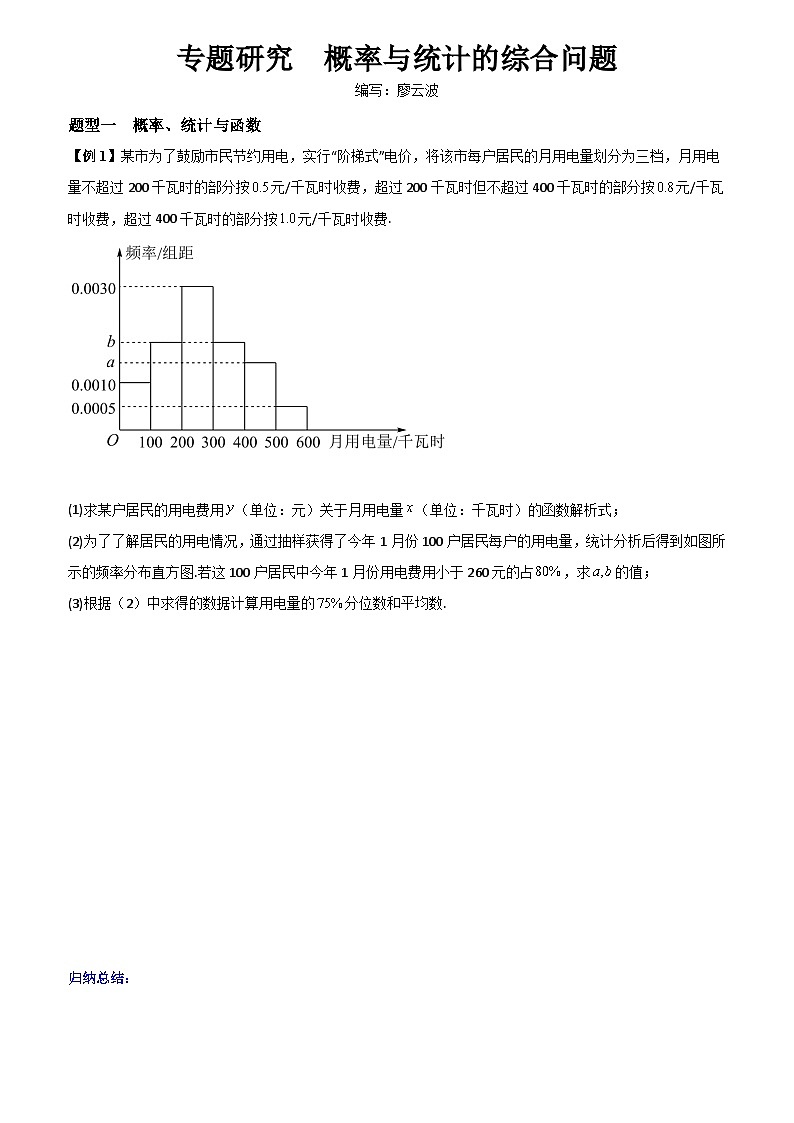
(2)为了了解居民的用电情况，通过抽样获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图.若这100户居民中今年1月份用电费用小于260元的占，求的值；
(3)根据（2）中求得的数据计算用电量的分位数和平均数.
归纳总结：
【练习1】某花店每天以每枝8元的价格从农场购进若干枝玫瑰花，然后以每枝18元的价格出售．如果当天卖不完，剩下的玫瑰花回收给农场，每枝可换取3元．花店记录了100天玫瑰花的日销量（单位：枝），整理得下表．
(1)若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天销量n（单位；枝，）的函数解析式；
(2)根据所列表格数据，以100天记录的日销量的频率作为概率．
①若花店两天的销量互不影响，求两天一共售出30枝玫瑰花的概率；
②若花店计划一天购进16枝或17枝玫瑰花，求两种情况下一天利润的分布列，并以两种情况的利润的期望值作为依据，判断应购进16枝还是17枝？
题型二 概率、统计与导数
【例2】2．随着中国经济的迅速发展，市场石料需求急增．西部某县有丰富的优质石料，当地政府决定有序开发本县石料资源．因建立石料厂会破坏生态，该县决定石料开发走“开发治理结合，人类生态友好”的路线.当地政府请国家环保机构每年对该县与石料开发相关的生态（以下简称生态）进行评估．若生态开始变差，则下一年石料厂将停产（本问题中，时间以整数年为单位），生态友好后复产．该县在建石料厂之初投入巨资进行与之有关的生态建设，考虑到可持续发展，这种生态投入（以下简称生态投入）将逐年减少（a是常数，）亿元．该县从2021年起，若某年生态友好，则下一年生态变差的概率是；若某年生态变差，则下一年生态友好的概率为．模型显示，生态变差的概率不大于0.16683时，该县生态将不再变差，生态投入结束．
(1)若2021年该县生态变差的概率为，求该县2022年生态友好的概率；
(2)若2021年该县生态变差概率为，生态投入是40亿元，a为何值时，从2021年开始到生态投入结束，对该县总生态投入额最小？并求出其最小值．
归纳总结：
【练习2】某盒子装有60个小球（除颜色之外其他完全相同），其中有若干黑球，其他均为白球．为了估计黑球的数目，设计如下实验：从盒子中有放回地抽取4个球，记录该次所抽取的黑球数目X，作为一次实验结果．进行上述实验共5次，记录下第i次实验中实际抽到黑球的数目．已知从该盒子中任意抽取一个球，抽到黑球的概率为．
(1)求X的分布列；
(2)实验结束后，已知第i次实验中抽到黑球的数目如下表所示．
设函数．
（ⅰ）求的极大值点；
（ⅱ）据（ⅰ）估计该盒子中黑球的数目，并说明理由．
题型三 概率、统计与数列
【例3】2022年4月23日是第27个“世界读书日”，某校组织“读书使青春展翅，知识让生命飞翔”主题知识竞赛，规定参赛同学每答对一题得2分，答错得1分，不限制答题次数.已知小明能正确回答每题的概率都为，且每次回答问题是相互独立的，记小明得分的概率为，.
(1)求，的值；
(2)求.
归纳总结：
【练习3】足球是一项大众喜爱的运动.2022卡塔尔世界杯揭幕战将在2022年11月21日打响，决赛定于12月18日晚进行，全程为期28天.
(1)为了解喜爱足球运动是否与性别有关，随机抽取了男性和女性各100名观众进行调查，得到22列联表如下：
依据小概率值a=0.001的独立性检验，能否认为喜爱足球运动与性别有关?
(2)校足球队中的甲、乙、丙、丁四名球员将进行传球训练，第1次由甲将球传出，每次传球时，传球者都等可能的将球传给另外三个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到．记开始传球的人为第1次触球者，第次触球者是甲的概率记为，即．
（i）求（直接写出结果即可）；
（ii）证明：数列为等比数列，并判断第19次与第20次触球者是甲的概率的大小．
【请完成课时作业（七十三）】
【课时作业（七十三）】
1.为响应“双减政策”，丰富学生课余生活，某校举办趣味知识竞答活动，每班各选派两名同学代表班级回答4道题，每道题随机分配给其中一个同学回答．小明，小红两位同学代表高二1班答题，假设每道题小明答对的概率为，小红答对的概率为，且每道题是否答对相互独立．记高二1班答对题目的数量为随机变量X．
(1)若，求x的分布列和数学期望；
(2)若高二1班至少答对一道题的概率不小于，求p的最小值．
2．一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代…，该微生物每代繁殖的个数是相互独立的，且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，．
(1)已知，，，，求；
(2)设表示该生物临近灭绝的概率，当时，证明：p是关于x的方程的最小正实根．
3．某科技公司新研制生产一种特殊疫苗，为确保疫苗质量，定期进行质量检验．某次检验中，从产品中随机抽取100件作为样本，测量产品质量体系中某项指标值，根据测量结果得到如下频率分布直方图：
（1）求频率分布直方图中a的值；
（2）技术分析人员认为，本次测量的该产品的质量指标值X服从正态分布，若同组中的每个数据用该组区间的中间值代替，计算，并计算测量数据落在内的概率；
（3）设生产成本为y元，质量指标值为x，生产成本与质量指标值之间满足函数关系假设同组中的每个数据用该组区间的中间值代替，试计算生产疫苗的平均成本．
参考数据：，则，．
4．一种掷骰子走跳棋的游戏：棋盘上标有第站、第站、第站、、第站，共站，设棋子跳到第站的概率为，一枚棋子开始在第站，棋手每掷一次骰子，棋子向前跳动一次．若掷出奇数点，棋子向前跳一站；若掷出偶数点，棋子向前跳两站，直到棋子跳到第站（获胜）或第站（失败）时，游戏结束（骰子是用一种均匀材料做成的立方体形状的游戏玩具，它的六个面分别标有点数、、、、、）．
(1)求、、，并根据棋子跳到第站的情况，试用和表示；
(2)求证：为等比数列；
(3)求玩该游戏获胜的概率．
日销量（枝）
14
15
16
17
18
19
20
频数
20
20
10
15
12
11
12
1
2
3
4
5
2
3
2
3
3
喜爱足球运动
不喜爱足球运动
合计
男性
60
40
100
女性
20
80
100
合计
80
120
200
专题研究 概率与统计的综合问题
编写：廖云波
题型一 概率、统计与函数
【例1】某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200千瓦时的部分按元/千瓦时收费，超过200千瓦时但不超过400千瓦时的部分按元/千瓦时收费，超过400千瓦时的部分按元/千瓦时收费.
(1)求某户居民的用电费用（单位：元）关于月用电量（单位：千瓦时）的函数解析式；
(2)为了了解居民的用电情况，通过抽样获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图.若这100户居民中今年1月份用电费用小于260元的占，求的值；
(3)根据（2）中求得的数据计算用电量的分位数和平均数.
【答案】(1)
(2)
(3)电量的分位数为375千瓦时.平均数275千瓦时
【分析】（1）根据题目条件，列出函数解析式即可；
（2）将代入（1）中解析式得到的值，再结合频率分布直方图求的值；
（3）根据百分位数和平均数的定义，结合频率分布直方图中的数据，计算即可.
（1）
当时，；
当时，；
当时，.
所以与之间的函数解析式为
（2）
由（1）可知，当时，，即用电量小于400千瓦时的占，
结合频率分布直方图可知，
解得.
（3）
设75%分位数为，
由题图知，用电量低于300千瓦时的频率为
，
用电量低于400千瓦时的频率为，
所以分位数在内，所以，解得，
即用电量的分位数为375千瓦时.
平均数= 千瓦时.
归纳总结：
【练习1】某花店每天以每枝8元的价格从农场购进若干枝玫瑰花，然后以每枝18元的价格出售．如果当天卖不完，剩下的玫瑰花回收给农场，每枝可换取3元．花店记录了100天玫瑰花的日销量（单位：枝），整理得下表．
(1)若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天销量n（单位；枝，）的函数解析式；
(2)根据所列表格数据，以100天记录的日销量的频率作为概率．
①若花店两天的销量互不影响，求两天一共售出30枝玫瑰花的概率；
②若花店计划一天购进16枝或17枝玫瑰花，求两种情况下一天利润的分布列，并以两种情况的利润的期望值作为依据，判断应购进16枝还是17枝？
【答案】(1)()
(2)①;②分布列见解析，应购进17枝.
【分析】（1）根据利润等于总收入减去进货总价，再加上退货收入即可得出答案；
（2）设购进16枝玫瑰花时，一天的利润为，写出的所有可能取值，根据表格求出对应概率，再根据期望公式求出的期望，同理求出购进17枝玫瑰花时，一天的利润为的期望，在比较期望的大小，即可得出结论.
(1)
当时，()；
当时，.
所以().
(2)
①当一天销量为14枝另一天销量为16枝时，
两天一共售出30枝玫瑰花的概率为，
当两天销量都是15枝时，
两天一共售出30枝玫瑰花的概率为，
所以两天一共售出30枝玫瑰花的概率为；
②若花店计划一天购进16枝玫瑰花时，设一天的利润为，
则可取，
，
，
，
则（元），
若花店计划一天购进17枝玫瑰花时，设一天的利润为，
则可取，
，
，
，
，
则（元），
因为，
所以应购进17枝.
题型二 概率、统计与导数
【例2】2．随着中国经济的迅速发展，市场石料需求急增．西部某县有丰富的优质石料，当地政府决定有序开发本县石料资源．因建立石料厂会破坏生态，该县决定石料开发走“开发治理结合，人类生态友好”的路线.当地政府请国家环保机构每年对该县与石料开发相关的生态（以下简称生态）进行评估．若生态开始变差，则下一年石料厂将停产（本问题中，时间以整数年为单位），生态友好后复产．该县在建石料厂之初投入巨资进行与之有关的生态建设，考虑到可持续发展，这种生态投入（以下简称生态投入）将逐年减少（a是常数，）亿元．该县从2021年起，若某年生态友好，则下一年生态变差的概率是；若某年生态变差，则下一年生态友好的概率为．模型显示，生态变差的概率不大于0.16683时，该县生态将不再变差，生态投入结束．
(1)若2021年该县生态变差的概率为，求该县2022年生态友好的概率；
(2)若2021年该县生态变差概率为，生态投入是40亿元，a为何值时，从2021年开始到生态投入结束，对该县总生态投入额最小？并求出其最小值．
【答案】(1)
(2)当时，对该县总生态投入额最小，最小值为亿元
【分析】（1）考虑到有“该县2021年生态友好，那么它2022年生态友好与该县年生态变差，而年生态友好”两种情况，故分别求出每种情况的概率，再根据互斥事件的概率公式求得答案;
（2）由题意推出该县从年开始的第年生态变差的概率，列出不等式求得，再求出对该县总生态总投入额的表达式，利用导数求得其最小值，可得答案.
(1)
设“该县2021年生态友好”，“该县2022年生态友好”，
∵该县2021年生态变差的概率为，即，，
∴如果该县2021年生态友好，那么它2022年生态友好的概率为
，
该县2021年变差，那么它2022年友好的概率为
．
因为“该县2021年生态友好，那么它2022年生态友好”与“该县年生态变差，而年生态友好”是互斥事件，
所以，,
所以，该县2022年生态友好的概率为．
(2)
设该县2021年生态变差的概率为,
同（1）可得，该县年生态友好的概率为，
∴该县年生态变差的概率为，
∴该县年生态变差的概率为，
该县从年开始的第年生态变差的概率为
,,
∴若从年开始到生态投入结束共有年，则，
即,
∴，
对该县总生态投入额
,
∴．
若，则，单调递减；若，则，单调递增,
由于时，，所以，当时，最小，且最小值是亿元,
也就是说，当时，对该县总生态投入额最小，最小值为亿元．
归纳总结：
【练习2】某盒子装有60个小球（除颜色之外其他完全相同），其中有若干黑球，其他均为白球．为了估计黑球的数目，设计如下实验：从盒子中有放回地抽取4个球，记录该次所抽取的黑球数目X，作为一次实验结果．进行上述实验共5次，记录下第i次实验中实际抽到黑球的数目．已知从该盒子中任意抽取一个球，抽到黑球的概率为．
(1)求X的分布列；
(2)实验结束后，已知第i次实验中抽到黑球的数目如下表所示．
设函数．
（ⅰ）求的极大值点；
（ⅱ）据（ⅰ）估计该盒子中黑球的数目，并说明理由．
【答案】(1)分布列见解析
(2)（ⅰ）；（ⅱ）39，理由见解析
【分析】（1）由，列出分布列；
（2）结合（1）得到，利用导数法求解；由取得最大值，即取得最大值，出现上述实验结果的概率最大求解．
(1)
由题可知．所以X的分布列为
(2)
（ⅰ）由（1）可知，
，
；
则．
令可得．
列表如下：
所以存在唯一极大值点；
（ⅱ）估计该盒子中黑球的数目为．理由如下：
由（ⅰ）可知，当且仅当时，取得最大值，即取得最大值，出现上述实验结果的概率最大，因此可以认为从盒子中任意抽取一个球，抽到黑球的概率为，从而估计该盒子中黑球的数目为39是合理的．
题型三 概率、统计与数列
【例3】2022年4月23日是第27个“世界读书日”，某校组织“读书使青春展翅，知识让生命飞翔”主题知识竞赛，规定参赛同学每答对一题得2分，答错得1分，不限制答题次数.已知小明能正确回答每题的概率都为，且每次回答问题是相互独立的，记小明得分的概率为，.
(1)求，的值；
(2)求.
【答案】(1)，
(2)
【分析】（1）由得2分即回答1题正确或者回答2题都错误，得3分即回答2题1题正确，1题错误或者回答3题都错误，根据互斥事件概率加法公式及相互独立事件概率乘法公式即可求解；
（2）由小明得分有两种情况，一种是小明在得分的情况下又答1题错误；另一种是小明在得分的情况下又答1题正确，可得，进而利用配凑法，根据等比数列的定义可得是以为首项，为公比的等比数列，则有，从而利用累加法可求.
(1)
解：得2分即回答1题正确或者回答2题都错误，所以，
得3分即回答2题1题正确，1题错误或者回答3题都错误，所以；
(2)
解：因为小明得分有两种情况，一种是小明在得分的情况下又答1题错误；
另一种是小明在得分的情况下又答1题正确.
所以，即，
因为，
所以，
因此是以为首项，为公比的等比数列，
所以，
当时，，
，
又符合上式，
所以.
归纳总结：
【练习3】足球是一项大众喜爱的运动.2022卡塔尔世界杯揭幕战将在2022年11月21日打响，决赛定于12月18日晚进行，全程为期28天.
(1)为了解喜爱足球运动是否与性别有关，随机抽取了男性和女性各100名观众进行调查，得到22列联表如下：
依据小概率值a=0.001的独立性检验，能否认为喜爱足球运动与性别有关?
(2)校足球队中的甲、乙、丙、丁四名球员将进行传球训练，第1次由甲将球传出，每次传球时，传球者都等可能的将球传给另外三个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到．记开始传球的人为第1次触球者，第次触球者是甲的概率记为，即．
（i）求（直接写出结果即可）；
（ii）证明：数列为等比数列，并判断第19次与第20次触球者是甲的概率的大小．
【答案】(1)喜爱足球运动与性别有关
(2)（i）；（ii）证明见解析，甲的概率大
【分析】（1）计算出卡方，与10.828比较得到结论；
（2）（i）根据传球的等可能性推出，（ii）推导出，构造出等比数列，
求出，得到，比较出大小.
（1）
假设：喜爱足球运动与性别独立，即喜爱足球运动与性别无关．
根据列联表数据，经计算得
根据小概率值的独立性检验，我们推断不成立，
即认为喜爱足球运动与性别有关，此推断犯错误的概率不超过0.001．
（2）
（i）由题意得：第二次触球者为乙，丙，丁中的一个，第二次触球者传给包括甲的三人中的一人，故传给甲的概率为，故．
（ii）第次触球者是甲的概率记为，则当时，第次触球者是甲的概率为，
第次触球者不是甲的概率为，
则，
从而，
又，是以为首项，公比为的等比数列．
则，
∴，，
，故第19次触球者是甲的概率大
【请完成课时作业（七十三）】
【课时作业（七十三）】
1.为响应“双减政策”，丰富学生课余生活，某校举办趣味知识竞答活动，每班各选派两名同学代表班级回答4道题，每道题随机分配给其中一个同学回答．小明，小红两位同学代表高二1班答题，假设每道题小明答对的概率为，小红答对的概率为，且每道题是否答对相互独立．记高二1班答对题目的数量为随机变量X．
(1)若，求x的分布列和数学期望；
(2)若高二1班至少答对一道题的概率不小于，求p的最小值．
【答案】(1)分布列见解析，数学期望为
(2)
【分析】（1）X的可能取值为0，1，2，3，4．，由二项分布求得各概率得分布列，由期望公式得期望；
（2）由对立事件的概率公式求得事件“至少答对一道题的概率”的概率，列不等式求解．
(1)
X的可能取值为0，1，2，3，4．
高二1班答对某道题的概率，
则，．
则X得分布列为
则．
(2)
高二1班答对某道题的概率为，
答错某道题的概率为．
则，解得，
所以p的最小值为．
2．一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代…，该微生物每代繁殖的个数是相互独立的，且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，．
(1)已知，，，，求；
(2)设表示该生物临近灭绝的概率，当时，证明：p是关于x的方程的最小正实根．
【答案】(1)1.1
(2)证明见解析
【分析】（1）根据期望公式直接计算可得；
（2）构造函数，利用导数讨论函数的单调性，结合，讨论可知.
(1)
由题知：，
(2)
因为
所以，p是方程的正实根
令，则
令，所以当时，
所以在区间上单调递增
又因为，
当时，
所以存在，使得
当时，，所以在上单调递减；
当时，，所以在上单调递增；
又因为，
所以在上存在唯一零点，
综上，所以p是方程的最小正实根
3．某科技公司新研制生产一种特殊疫苗，为确保疫苗质量，定期进行质量检验．某次检验中，从产品中随机抽取100件作为样本，测量产品质量体系中某项指标值，根据测量结果得到如下频率分布直方图：
（1）求频率分布直方图中a的值；
（2）技术分析人员认为，本次测量的该产品的质量指标值X服从正态分布，若同组中的每个数据用该组区间的中间值代替，计算，并计算测量数据落在内的概率；
（3）设生产成本为y元，质量指标值为x，生产成本与质量指标值之间满足函数关系假设同组中的每个数据用该组区间的中间值代替，试计算生产疫苗的平均成本．
参考数据：，则，．
【答案】（1）；（2）；；（3）元．
【分析】（1）由频率之和等于1求出a的值；
（2）先由频率分布直方图求平均数的方法得出，再由参考数据得出数据落在内的概率；
（3）先由频率分布直方图得出每组的质量指标值，再根据生产成本与质量指标值之间的函数关系得出生产疫苗的平均成本．
【详解】解：（1）由
解得．
（2）依题意，
故
所以
故测量数据落在内的概率约为
（3）根据题意得
故生产该疫苗的平均成本为．
【点睛】关键点睛：解决问题二的关键在于由频率分布直方图计算平均数的方法得出，进而由正态分布的性质得出概率.
4．一种掷骰子走跳棋的游戏：棋盘上标有第站、第站、第站、、第站，共站，设棋子跳到第站的概率为，一枚棋子开始在第站，棋手每掷一次骰子，棋子向前跳动一次．若掷出奇数点，棋子向前跳一站；若掷出偶数点，棋子向前跳两站，直到棋子跳到第站（获胜）或第站（失败）时，游戏结束（骰子是用一种均匀材料做成的立方体形状的游戏玩具，它的六个面分别标有点数、、、、、）．
(1)求、、，并根据棋子跳到第站的情况，试用和表示；
(2)求证：为等比数列；
(3)求玩该游戏获胜的概率．
【答案】(1)，，，且.
(2)证明见解析
(3)
【分析】（1）根据题意可直接求得、、，然后讨论棋子跳到第站，所包括两种情形，可得出关于和的表达式；
（2）计算得出，结合等比数列的定义可证得结论成立；
（3）求得，利用累加法可求得，即可得解.
(1)
解：棋子开始在第站是必然事件，所以，
棋子跳到第站，只有一种情形，第一次掷骰子出现奇数点，其概率为，所以；
棋子跳到第站，包括两种情形，①第一次掷骰子出现偶数点，其概率为；②前两次掷骰子都出现奇数点，其概率为，所以；
棋子跳到第站，包括两种情形，①棋子先跳到第站，又掷骰子出现偶数点，其概率为；
②棋子先跳到第站，又掷骰子出现奇数点，其概率为，
故，
棋子跳到站只有一种情况，棋子先跳到第站，又掷骰子出现偶数点，其概率为，所以，.
(2)
证明：由（1）可得且，
所以，数列为等比数列，且公比为.
(3)
解：由（2）可知，
所以，
.
所以，玩该游戏获胜的概率为.
日销量（枝）
14
15
16
17
18
19
20
频数
20
20
10
15
12
11
12
1
2
3
4
5
2
3
2
3
3
X
0
1
2
3
4
P
区间
符号
正
负
递增
递减
喜爱足球运动
不喜爱足球运动
合计
男性
60
40
100
女性
20
80
100
合计
80
120
200
X
0
1
2
3
4
P