

所属成套资源:高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)(原卷版+解析)
- 高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第08课时直线与双曲线的位置关系(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第08课时离散型随机变量的分布列、均值与方差(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第09课时n次独立重复试验与二项分布(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第09课时抛物线及其性质(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第9课时函数与方程(原卷版+解析) 试卷 0 次下载
高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第8课时函数的图像(原卷版+解析)
展开
这是一份高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第8课时函数的图像(原卷版+解析),共37页。
【回归教材】
1.平移变换
①函数的图像是把函数的图像沿轴向 个单位得到的;
②函数的图像是把函数的图像沿轴向 个单位得到的;
③函数的图像是把函数的图像沿轴向 个单位得到的;
④函数的图像是把函数的图像沿轴向 个单位得到的;
2.对称变换
①函数与函数的图像关于 对称;
函数与函数的图像关于 对称;
函数与函数的图像关于坐标 对称;
②的图像是将函数的图像保留轴上方的部分不变,将轴下方的部分关于轴对称翻折上来得到的(如图(a)和图(b))所示
③的图像是将函数的图像只保留轴右边的部分不变,并将右边的图像关于轴对称得到函数左边的图像即函数是一个偶函数(如图(c)所示).
④函数与的图像关于 对称.
3.伸缩变换
①的图像,可将的图像上的每一点的 伸长或缩短 到原来的倍得到.
②的图像,可将的图像上的每一点的 伸长或缩短 到原来的倍得到.
【方法技巧与总结】
(1)若恒成立,则的图像关于直线 对称.
(2)设函数定义在实数集上,则函数与的图象关于直线 对称.
(3)若,对任意恒成立,则的图象关于直线 对称.
(4)函数与函数的图象关于直线 对称.
(5)函数与函数的图象关于直线 对称.
(6)函数与函数的图象关于点 中心对称.
(7)函数平移遵循自变量“左加右减”,函数值“上加下减”.
【典例讲练】
题型一 作出函数图像
【例1-1】已知函数.
(1)用分段函数的形式表示函数f(x); (2)画出函数f(x)的图象,并写出函数f(x)的值域.
【例1-2】已知函数
(1)在所给的直角坐标系内画出的图象并写出的单调区间;
(2)求不等式的解集.
【练习1-1】已知函数
请在给定的坐标系中画出此函数的图象,并根据图象说出函数的值域及单调减区间
题型二 图形的变换
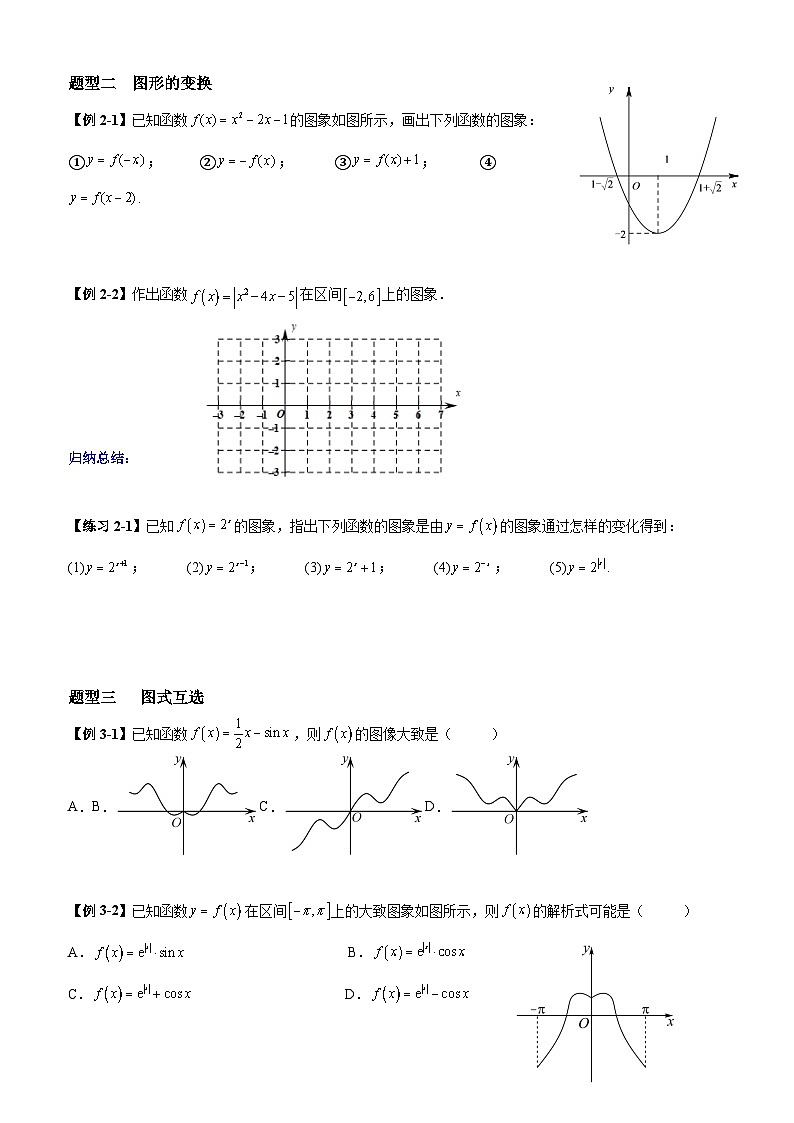
【例2-1】已知函数的图象如图所示,画出下列函数的图象:
①; ②; ③; ④.
【例2-2】作出函数在区间上的图象.
归纳总结:
【练习2-1】已知的图象,指出下列函数的图象是由的图象通过怎样的变化得到:
(1); (2); (3); (4); (5).
题型三 图式互选
【例3-1】已知函数,则的图像大致是( )
A.B.C.D.
【例3-2】已知函数在区间上的大致图象如图所示,则的解析式可能是( )
A. B.
C.D.
【练习3-1】函数的大致图象是( )
A. B. C.D.
题型四 函数图象的应用
【例4-1】已知,,若,则的最值是( )
最大值为3,最小值B.最大值为,无最小值
C.最大值为3,无最小值D.无最大值,最小值为
【例4-2】【多选题】若函数()是周期为2的奇函数.则下列选项一定正确的是( )
A.函数的图象关于点对称 B.2是函数的一个周期
C. D.
【例4-3】已知函数若函数有2个零点,则实数的取值范围是( )
A.B.C.D.
【练习4-1】【多选题】已知函数,若函数恰有3个零点,则m的取值可能是( )
A.B.C.D.
【练习4-2】已知函数,如果互不相等的实数,满足,则实数的取值范围_____.
【练习4-3】已知定义在R上的函数满足,且是奇函数,则( )
A.是偶函数 B.的图象关于直线对称
C.是奇函数 D.的图象关于点对称 【请完成课时作业(十四)】
【课时作业(十四)】
A组 基础题
1.函数的图象大致为( )
A. B. C. D.
2.若函数满足,则下列函数中为奇函数的是( )
A.B.C.D.
3.如右图所示是一鱼缸的轴截面图,已知该鱼缸装满水时储水量为V,缸高为H,其底部破了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是( )
A.B.C.D.
4.已知函数的图象如图所示,则下列说法错误的是( )
A. B.
C. D.
5.将函数的图像向左、向下各平移1个单位长度,得到的函数图像,则( )
A. B. C. D.
6.已知函数关于x的方程有3个不同的解,则a的取值范围是( )
A.B.C.D.
7.已知函数,则满足不等式的的取值范围是( )
A.B.C.D.
8.已知函数的定义域为,为奇函数,为偶函数,则( )
A.B.C.D.
9.【多选题】已知定义在上的函数满足条件,且函数为奇函数,下列有关命题的说法正确的是( )
A.为周期函数B.为上的偶函数
C.为上的单调函数D.的图象关于点对称
10.【多选题】已知函数,若有三个不等实根,且,则( )
A.的单调递减区间为B.的取值范围是
C.的取值范围是D.函数有4个零点
11.已知函数.
(1)求的单调区间; (2)求在区间上的最大值和最小值;
(3)画出的函数图像(标出极值点).
B组 能力提升能
1.已知函数,若方程有4个不同的根,,,,且,则的取值范围是( )
A.B.C.D.
2.已知函数的图像如右图所示,则函数的解析式可能是( )
A. B. C.D.
3.函数是R上的奇函数,函数图像与关于对称,则( )
A.0B.-1C.2D.1
4.【多选题】记实数中的最大数为,最小数为,则关于函数的说法中正确的是( )
A.方程有三个根B.的单调减区间为和
C.的最大值为D.的最小值为
第 8 课时 函数的图像
编写:廖云波
【回归教材】
1.平移变换
①函数的图像是把函数的图像沿轴向左平移个单位得到的;
②函数的图像是把函数的图像沿轴向右平移个单位得到的;
③函数的图像是把函数的图像沿轴向上平移个单位得到的;
④函数的图像是把函数的图像沿轴向下平移个单位得到的;
2.对称变换
①函数与函数的图像关于轴对称;
函数与函数的图像关于轴对称;
函数与函数的图像关于坐标原点对称;
②的图像是将函数的图像保留轴上方的部分不变,将轴下方的部分关于轴对称翻折上来得到的(如图(a)和图(b))所示
③的图像是将函数的图像只保留轴右边的部分不变,并将右边的图像关于轴对称得到函数左边的图像即函数是一个偶函数(如图(c)所示).
④函数与的图像关于对称.
3.伸缩变换
①的图像,可将的图像上的每一点的纵坐标伸长或缩短 到原来的倍得到.
②的图像,可将的图像上的每一点的横坐标伸长或缩短 到原来的倍得到.
【方法技巧与总结】
(1)若恒成立,则的图像关于直线对称.
(2)设函数定义在实数集上,则函数与的图象关于直线对称.
(3)若,对任意恒成立,则的图象关于直线对称.
(4)函数与函数的图象关于直线对称.
(5)函数与函数的图象关于直线对称.
(6)函数与函数的图象关于点中心对称.
(7)函数平移遵循自变量“左加右减”,函数值“上加下减”.
【典例讲练】
题型一 作出函数图像
【例1-1】已知函数.
(1)用分段函数的形式表示函数f(x);
(2)画出函数f(x)的图象,并写出函数f(x)的值域.
【答案】(1)
(2)作图见解析,的值域为
【解析】
【分析】
(1)根据零点分段法去绝对值,由此将表示为分段函数的形式.
(2)根据的解析式画出的图象,结合图象求得的值域.
(1)
当时,,
当时,,
所以.
(2)
由(1)得,由此画出的图象如下图所示:
由图像知,的值域为.
【例1-2】已知函数
(1)在所给的直角坐标系内画出的图象并写出的单调区间;
(2)求不等式的解集.
【答案】(1)图象见解析,单调递增区间为,单调递减区间为;
(2).
【解析】
【分析】
(1)根据解析式得到函数图象的坐标列表,在坐标系中描点画出函数图象,结合图象确定单调区间即可.
(2)求对应自变量值,再结合图象求不等式的解集.
(1)
由解析式知:
的图象如下图所示:
由图象知,的单调递增区间为,单调递减区间为.
(2)
令,解得或,
结合图象知:的解集为.
归纳总结:
【练习1-1】已知函数
(1)求的值;
(2)若,求的值;
(3)请在给定的坐标系中画出此函数的图象,并根据图象说出函数的值域及单调减区间
【答案】(1)
(2)或
(3)值域为,减区间为,,
【解析】
【分析】
(1)分段函数求值,根据自变量所在区间代相应对应关系(2)分类讨论即可求解(3)分段函数图象分段作
(1)
因为
所以
(2)
当时,,不合题意,应舍去
当时,
解之得或(舍)
当时,,则
综上,或
(3)
值域为
减区间为,,
题型二 图形的变换
【例2-1】已知函数的图象如图所示,画出下列函数的图象:
①; ②;
③; ④.
【答案】(1)函数与的图象关于y轴对称.
(2)答案见解析.
【解析】
【分析】
(1)从图象上的点的变换可以推导出图象的变换;(2)①是原图象关于y轴对称得到的;②是原图象关于x轴对称得到的;③是原图象向上平移一个单位长度得到的;④是原图象向右平移两个单位长度得到的.
【详解】
(1)函数与的图象关于y轴对称.
理由如下:在上任取一点,所以,可得点在的图象上,点和点关于y轴对称,所以函数与的图象关于y轴对称.
(2)①,如图1
②,如图2
③,如图3
④,如图4
【例2-2】作出函数在区间上的图象.
【答案】作图见解析
【解析】
【分析】
先作二次函数的图象,然后取绝对值变换,轴下方图象沿轴翻折上来,再截取区间的部分.
【详解】
解:先作出二次函数的图象,再把图象在轴下方的部分沿轴翻折到轴上方,保留轴上及其上方的部分,并截取在区间的部分,即得函数的图象,如图所示.
归纳总结:
【练习2-1】已知的图象,指出下列函数的图象是由的图象通过怎样的变化得到:
(1);
(2);
(3);
(4);
(5).
【答案】(1)向左平移1个单位;
(2)向右平移1个单位;
(3)向上平移1个单位;
(4)关于轴对称;
(5)保留时,的图象,再作关于轴对称.
【解析】
【分析】
根据指数函数的图象和函数图象的平移变换的特点,即可得出答案.
(1)
解:的图象是由的图象向左平移1个单位得到.
(2)
解:的图象是由的图象向右平移1个单位得到.
(3)
解:的图象是由的图象向上平移1个单位得到.
(4)
解:∵与的图象关于轴对称,
∴作的图象关于轴的对称图形便可得到的图象.
(5)
解:∵为偶函数,故其图象关于轴对称,
故先作出当时,的图象,再作关于轴的对称图形,即可得到的图象.
题型三 图式互选
【例3-1】已知函数,则的图像大致是( )
A.B.
C.D.
【答案】A
【解析】
【分析】
根据的奇偶性和的符号可选出答案.
【详解】
因为,所以是奇函数,故排除BD,
因为,所以可排除C,
故选:A
【例3-2】已知函数在区间上的大致图象如图所示,则的解析式可能是( )
A.B.
C.D.
【答案】B
【解析】
【分析】
分析图像的特点即可判断.
【详解】
由图可知,函数 是关于y轴对称的偶函数,当x=0时, ,
当 时, ,
对于A, 是奇函数,不符合题意;
对于B, 是偶函数, , ,符合题意;
对于C, 是偶函数, ,不符合题意;
对于D, 是偶函数, ,不符合题意;
故选:B.
归纳总结:
【练习3-1】函数的大致图象是( )
A.B.
C.D.
【答案】B
【解析】
【分析】
利用导数求出函数的单调区间,即可判断;
【详解】
解:因为,所以,
当时,当或时,
即在上单调递增,在、上单调递减,结合图象可知只有B符合题意.
故选:B
题型四 函数图象的应用
【例4-1】已知,,若,则的最值是( )
最大值为3,最小值B.最大值为,无最小值
C.最大值为3,无最小值D.无最大值,最小值为
【答案】B
【解析】
【分析】
作出的图象,其实表示的是较小的值.如图实线部分,知有最大值而无最小值,且最大值不是3,故可得答案.
【详解】
解:根据已知条件,可以求出,
如图所示,在A处取得最大值,没有最小值.
由得.
所以有最大值,无最小值.
故选:B.
【例4-2】【多选题】若函数()是周期为2的奇函数.则下列选项一定正确的是( )
A.函数的图象关于点对称
B.2是函数的一个周期
C.
D.
【答案】AC
【解析】
【分析】
本题考查抽象函数的对称性与周期性,利用函数是奇函数得到关系式和,即可逐个判断出选项.
【详解】
函数是奇函数,,函数图象关于点对称,故A正确;
函数是周期为2,所以的周期为4,故B错误;
函数是周期为2的奇函数, ,故C正确;
,无法判断的值,故D错误.
故选:AC.
【例4-3】已知函数若函数有2个零点,则实数的取值范围是( )
A.B.C.D.
【答案】A
【解析】
【分析】
根据的性质画出函数图像,将问题化为与有2个交点,数形结合求的范围.
【详解】
由题意,与有2个交点,
当时,递增且值域为;
当时,在上递减,上递增且值域为;
所以的图像如下:
由图知:时,有2个零点.
故选:A
归纳总结:
【练习4-1】【多选题】已知函数,若函数恰有3个零点,则m的取值可能是( )
A.B.C.D.
【答案】AD
【解析】
【分析】
利用导数研究函数的性质,作出函数的大致图象,利用数形结合可得.
【详解】
依题意可得的图象与直线有3个公共点.
∵函数,
∴,
当时,单调递增;当时,单调递减;
当时,单调递减;当时,单调递增.
故的极小值为,极大值为.
作出的大致图象,如图所示,
由图可知,m的取值范围是.
故选:AD.
【练习4-2】已知函数,如果互不相等的实数,满足,则实数的取值范围_____.
【答案】
【解析】
【分析】
画出函数图象,数形结合得到,,从而求出的取值范围.
【详解】
,画出函数图象,如图所示:不妨设,其中,故,且,所以的取值范围是.
故答案为:
【练习4-3】已知定义在R上的函数满足,且是奇函数,则( )
A.是偶函数B.的图象关于直线对称
C.是奇函数D.的图象关于点对称
【答案】C
【解析】
【分析】
由周期函数的概念易知函数的周期为2,根据图象平移可得的图象关于点对称,进而可得奇偶性.
【详解】
由可得2是函数的周期,
因为是奇函数,所以函数的图象关于点对称,
所以,,所以是奇函数,
故选:C.
【请完成课时作业(十四)】
【课时作业(十四)】
A组 基础题
1.函数的图象大致为( )
A.B.
C.D.
【答案】A
【解析】
【分析】
判断函数的奇偶性排除两个选项,再结合特殊的函数值排除一个选项后得正确结论.
【详解】
由题可得函数定义域为,且,故函数为奇函数,故排除BD,
由,,故C错误,
故选:A.
2.若函数满足,则下列函数中为奇函数的是( )
A.B.C.D.
【答案】D
【解析】
【分析】
首先得到关于对称,再根据函数平移规则得到关于对称,即可判断;
【详解】
解:因为,所以关于对称,所以将向左平移一个单位,再向上平移一个单位得到函数,该函数的对称中心为,故为奇函数,
故选:D
3.如图所示是一鱼缸的轴截面图,已知该鱼缸装满水时储水量为V,缸高为H,其底部破了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是( )
A.B.C.D.
【答案】B
【解析】
【分析】
利用函数的单调性和变化率分析判断得解.
【详解】
由题得是增函数,曲线的变化率是先慢慢变大,后慢慢变小.
故选:B.
4.已知函数的图象如图所示,则下列说法错误的是( )
A.B.
C.D.
【答案】C
【解析】
【分析】
根据函数图象,判断函数的奇偶性、周期性、对称性等性质,逐项判断即可.
【详解】
解:由函数的图象可得,函数为偶函数,函数关于对称,且最小正周期为2,最大值为1,最小值为0,
A项中,,故A项正确;
B项中,,故B项正确;
C项中,因为,则函数的周期为1,而函数的最小正周期为2,故C项错误.
D项中,,则函数关于对称,故D项正确.
故选:C.
5.将函数的图像向左、向下各平移1个单位长度,得到的函数图像,则( )
A.B.
C.D.
【答案】B
【解析】
【分析】
根据函数的图象变换的原则,结合对数的运算性质,准确运算,即可求解.
【详解】
由题意,将函数的图像向左、向下各平移1个单位长度,
可得.
故选:B.
6.已知函数关于x的方程有3个不同的实数解,则a的取值范围是( )
A.B.C.D.
【答案】B
【解析】
【分析】
由题意可得:与有三个交点,结合图象分析,并把代入检验.
【详解】
由题意可得:与有三个交点
如图,当时,符合题意
当时,与只有一个交点
令,则或
∴,符合题意
综上所述:
故选:B.
7.已知函数,则满足不等式的的取值范围是( )
A.B.C.D.
【答案】C
【解析】
【分析】
先画出图象,结合图象得到或,解不等式即可.
【详解】
画出的图象如图所示,要使不等式成立,必有或,
由可得;由可得,综上可得.
故选:C.
8.已知函数的定义域为,为奇函数,为偶函数,则( )
A.B.C.D.
【答案】A
【解析】
【分析】
根据函数图象之间的平移变换及所给奇、偶函数判断A,给出满足条件的特殊函数排除BCD.
【详解】
因为为奇函数,
所以的图象经过原点,即,
由的图象向右平移2个单位可得函数的图象知,图象过点,
即,
因为为偶函数,所以,
所以当时,,故A正确;
令,则满足为奇函数,为偶函数,
显然BCD不满足.
故选:A
9.【多选题】已知定义在上的函数满足条件,且函数为奇函数,下列有关命题的说法正确的是( )
A.为周期函数B.为上的偶函数
C.为上的单调函数D.的图象关于点对称
【答案】ABD
【解析】
【分析】
由周期性的定义可判断A,由奇偶性的定义可判断B,由偶函数的单调性的特点可判断C,由奇函数的对称性结合图像平移可判断D
【详解】
对于:函数,
是周期为的函数,故正确;
对于B:,
即
又的周期为,
又是奇函数,
,令,则
是偶函数,即是偶函数,故B正确;
对于C:由B知是偶函数,
在和上的单调性相反,
在上不单调,故C错误;
对于D:函数为奇函数,
的图象关于点对称,
的函数图象是由的图象向右平移个单位得到的,
的函数图象关于点对称,故D正确.
故选:ABD
10.【多选题】已知函数,若有三个不等实根,且,则( )
A.的单调递减区间为B.的取值范围是
C.的取值范围是D.函数有4个零点
【答案】ACD
【解析】
【分析】
作出函数和有三个交点的图象,结合图象逐个判断即可求解
【详解】
作出函数和有三个交点的图象,
可知,的单调递减区间为,故A正确;
的取值范围是,故B错误;
由,得,即,
故,则.
又因为,所以的取值范围为,故C正确;
令,则或,
则函数的零点可转化为或的零点,
由图象可知只有一个零点,有3个零点,
即函数有4个零点,故D正确;
故选:ACD
11.已知函数.
(1)求的单调区间;
(2)求在区间上的最大值和最小值;
(3)画出的草图(要求尽量精确).
【答案】(1)增区间为,减区间为;
(2)最小值为,最大值为;
(3)图象见解析.
【解析】
【分析】
(1)利用导数研究的单调性,即可得单调区间;
(2)由(1)确定区间单调性,并得到极值、端点值,进而得到最值.
(3)五点法画出函数图象.
(1)
由题设,
所以、上,上,
所以的单调增区间为、,单调减区间为.
(2)
由(1)可得如下列表:
当时,在的最小值为,
当或时,在的最大值为.
(3)
结合(1)的结论,函数图象如下:
B组 能力提升能
1.已知函数,若方程有4个不同的根,,,,且,则的取值范围是( )
A.B.C.D.
【答案】D
【解析】
【分析】
作出函数与的图像,得到关于对称,化简条件,利用对勾函数的性质可求解.
【详解】
作函数与的图像如下:
方程有4个不同的根,,,,且,
可知关于对称,即,且,
则,即,则
即,则;
当得或,则;;
故,;
则函数,在上为减函数,在上为增函数;
故取得最小值为,而当时,函数值最大值为.
即函数取值范围是.
故选:D.
【点睛】
本题主要考查了分段函数的运用,主要考查函数的单调性的运用,运用数形结合的思想方法是解题的关键,属于难题.
2.已知函数的图像如图所示,则函数的解析式可能是( )
A.B.
C.D.
【答案】C
【解析】
【分析】
从奇偶性分析,排除BD选项,求导研究函数单调性,排除A选项,C选项满足要求.
【详解】
从图像可以看出关于原点对称,为奇函数,
B选项,定义域为R,且
,为偶函数,排除B;
D选项,定义域为R,且,为偶函数,排除D;
A选项,,
当时,,即单调递减,显然与图像不符,排除A;
C选项,定义域为R,且,为奇函数,且经检验,符合函数的单调性,故C为正确答案.
故选:C
3.函数是R上的奇函数,函数图像与函数关于对称,则( )
A.0B.-1C.2D.1
【答案】C
【解析】
【分析】
由函数是R上的奇函数,可得函数的图像关于点对称,根据条件可得函数的图像关于对称,从而得出答案.
【详解】
函数是R上的奇函数,则
设,则,则函数的图像关于点对称
函数图像与函数关于对称,
所以函数的图像关于对称,所以
故选:C
4.【多选题】记实数中的最大数为,最小数为,则关于函数的说法中正确的是( )
A.方程有三个根B.的单调减区间为和
C.的最大值为D.的最小值为
【答案】AC
【解析】
【分析】
由的定义可得图象,结合图象依次判断各个选项即可.
【详解】
由的含义可得图象如下图所示,
由图象可知:
对于A,与有且仅有三个不同交点,即有三个根,A正确;
对于B,的单调递减区间为和,B错误;
对于C,,C正确;
对于D,无最小值,D错误.
故选:AC.
0
1
2
3
4
5
0
0
0
0
0
4
7
递增
递减
递增
0
4
7
4
相关试卷
这是一份高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第05课时椭圆及其性质(原卷版+解析),共36页。
这是一份高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第4课时复数(原卷版+解析),共23页。
这是一份高考数学一轮复习【考点题型归纳讲练】导学案(新高考专用)第04课时排列与组合(原卷版+解析),共27页。










