数学4.2 不等式的基本性质说课ppt课件

这是一份数学4.2 不等式的基本性质说课ppt课件，共21页。PPT课件主要包含了等式有哪些性质，你发现了什么规律，-2x，AB＞AC－BC等内容，欢迎下载使用。
1. 能通过探究，归纳出不等式的基本性质1； 2. 能用不等式的基本性质1对不等式进行变形； 3. 理解不等式的移项的概念，初步学会移项的方法； 4. 经历把不等式变形的过程，培养思维的灵活性.
等式性质1 等式两边都加上(或减去)同一个数(或式)，所得结果仍是等式.
等式性质2 等式两边都乘(或除以)同一个数(或式)(除数或除式不能为0)，所得结果仍是等式.
不等式有什么性质呢？运用等式的性质可以对等式变形，运用不等式的性质如何对不等式变形呢？
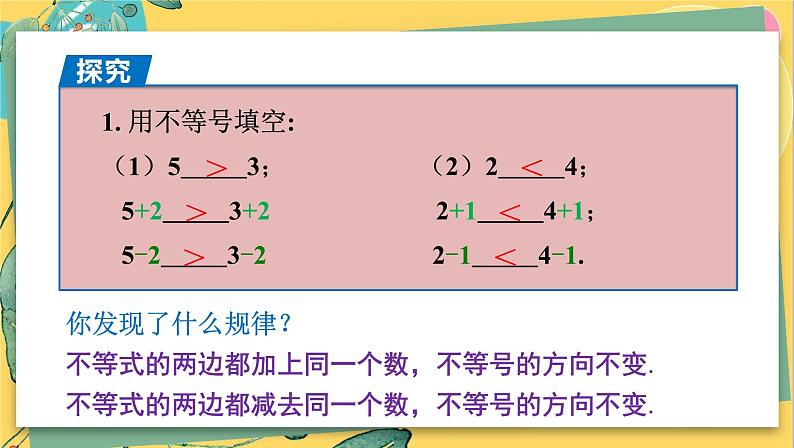
不等式的两边都加上同一个数，不等号的方向不变.
不等式的两边都减去同一个数，不等号的方向不变.
不等式两边都加上或减去同一个式子，不等号方向不变.
同问题1一样，我们发现：不等式的两边都加上(或减去)同一个数，不等号的方向不变.
综合所述我们得到，一般地，不等式具有如下性质：
即， 如果a＞b，那么a+c＞b+c， a-c＞b-c.
例1 用“＞”或“＜”填空：(1) 已知a＞b，则a+3 b+3；(2) 已知a＜b，则a-5 b-5.
解：(1)因为a＞b，所以两边都加上3，由不等式性质1，得 a+3＞b+3.
(2) 因为a＜b，两边都减去5，由不等式性质1，得a-5＜b-5.
解：(1)根据由不等式性质1，可得x+6 ＞5 ，
例2 把下列不等式化为x＞a或x＜a的形式：(1) x+6＞5； (2) 3x＜2x-2.
即 x＞-1.
由上可知，在不等式的两边都减去-6，不等式的左边就只有含未知数的项，从而把不等式化为x＞a的形式.
解：(2)根据由不等式性质1，可得3x ＜2x-2 ，
例2 把下列不等式化为x＞a或x＜a的形式：(1) x+6＞5； (2) 3x＜-2.
即 x＜-2.
由上可知，在不等式的两边都减去-2x，就只有不等式的左边含有未知数x的项了，而右边含未知数x的项没有了。从而把不等式化成x＜a的形式.
其实，对于(2)的化简过程，不等式两边同时减去2x，就是把3x＜2x-2作了如下变形：
这种变形就是把不等式一边的某一项变号后移到另一边，我们把这种变形称为移项.
根据不等式基本性质1，我们可以把不等式AB+BC＞AC中的BC移动右边，得
同理， AB－AC＜BC， BC－AB＜AC.
即 AC－BC＜AB.
由此可得，三角形任意两边之差小于第三边.
1. 用不等号填空： (1)若x+2≥9，则x 7； (2) 若x+2y≤y，则x 7； (3) 若x＞3y，则x+m 3y+m； (4)若x＜3y，则3y+4 x+1.
解析：根据不等式性质1，在不等式x+7＞-5 两边都减去2x得x+7＞-5，故A正确，选A。
2. 若3x+7＞2x-5，则下列不等式中正确的是（ ） A. x+7＞-5 B. 3x+7＞2x+2 C. 3x＞2x-12 D. 3x+2＞2x
3. 若a＜b＜c，则下列不等式中错误的是（ ） A. a+c＜b+c B. a+2c＜b+2c C. a-c＜b-c D. b-a＜c-b
解析：根据不等式性质1，A，B，C正确。而D是在不等式b＜c的两边减去不同的数，不符合不等式性质1，因此是错误的，故选D.
4. 下面不等式中，移项正确的是 （ ） A. 把-3x+1≤x-3移项得-3x+x≤-3+1 B. 把x-3≥2x-3移项得x-2x≥-3-3 C. 把4-y＜2y+5移项得y-2y≥5-4 D. 把6-2y＞7y+5移项得-2y-7y＞5-6
解析：不等式的移项，一定要把从一边移到另一边的项改变符号，而不移动到另一边的项就不能改变符号.
1. 不等式的性质1是什么？
不等式的两边都加上(或减去)同一个数(或式)，不等号的方向不变。
2. 什么叫做不等式的移项？移项应注意什么？
把不等式一边的某一项变号后移到另一边，叫做不等式的移项.注意：移项要变号.
3. 如何把不等式化为x＞a或x＜a的形式？
把含未知数的项移到不等式的左边，把常数项移到右边，然后合并同类项。
4. 三角形任意一边与另外两边的和、差有何大小关系？
三角形任意一边大于另两边的差，而小于另两边的和.
可表示为 b-c＜a＜b+c，a-c＜b＜a+c，a-b＜c＜a+b.
第131页课后练习第1、2题：
1. 已知a ＜ b ，用“＞”或“＜”填空：(1) a+12 b+12； (2) b-10 a-10.