广东省惠州市惠东县2023-2024学年八年级下学期期末数学试题(无答案)

这是一份广东省惠州市惠东县2023-2024学年八年级下学期期末数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
本试卷共4页，23小题，满分120分．考试用时120分钟．
一、选择题：本大题10小题，每小题3分，共30分。在每小题列出的四个选项中，只有一个是符合题目要求的．
1．下列根式是最简二次根式的是（ ）
A．B．C．D．
2．下列函数是正比例函数的是（ ）
A．B．C．D．
3．如图，在平行四边形中，，，的平分线交于，交的延长线于点，则（ ）
第3题图
A．4B．3C．2D．1
4．“1000米跑”是体育中考男生必考项目，体育老师一声令下，小明立即开始慢慢加速，途中一直保持匀速，最后400米时奋力冲刺跑完全程，下列最符合小明跑步时的速度（单位：米／分）与时间（单位：分）之间的大致图象的是（ ）
A．B．
C．D．
5．某校要从三名学生中选取一位参加县中学生体育运动会的跳远项目，对甲、乙、丙3位同学的跳远成绩进行了分析，这3位同学三次跳远平均成绩大致相同，他们的方差分别是，，，则这3位同学三次跳远成绩发挥最稳定的是（ ）
A．甲B．乙C．丙D．无法确定
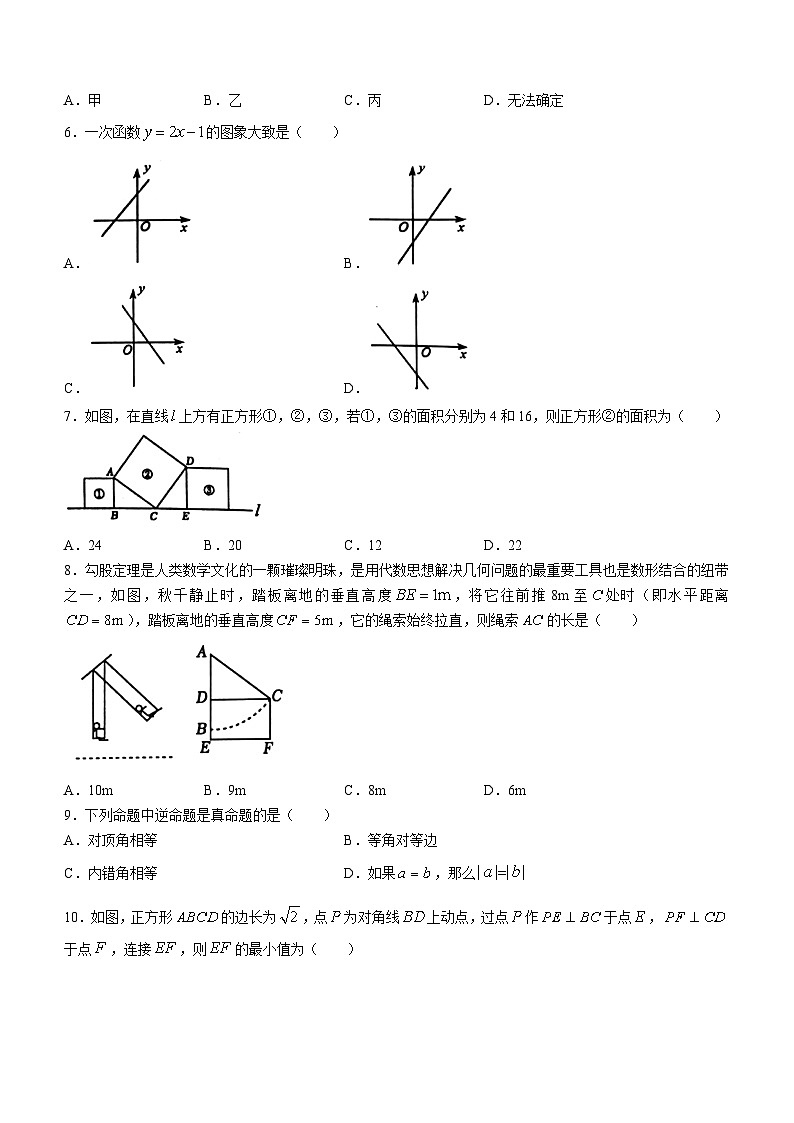
6．一次函数的图象大致是（ ）
A．B．
C．D．
7．如图，在直线上方有正方形①，②，③，若①，③的面积分别为4和16，则正方形②的面积为（ ）
A．24B．20C．12D．22
8．勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题的最重要工具也是数形结合的纽带之一，如图，秋千静止时，踏板离地的垂直高度，将它往前推8m至处时（即水平距离），踏板离地的垂直高度，它的绳索始终拉直，则绳索的长是（ ）
A．10mB．9mC．8mD．6m
9．下列命题中逆命题是真命题的是（ ）
A．对顶角相等B．等角对等边
C．内错角相等 D．如果，那么
10．如图，正方形的边长为，点为对角线上动点，过点作于点，于点，连接，则的最小值为（ ）
A．2B．4C．D．1
二、填空题：本大题5小题，每小题3分，共15分．
11．使代数式有意义的的取值范围是________．
12．化简：_________．
13．如图，点是直线上的一点．已知▱的面积为，则的面积为________．
第13题图
14．如图，直线经过点，则不等式的解集为_________．
第14题图
15．如图，在中，是边上的中点，过点作一条直线，交的平分线于点，交外角的平分线于点．当时，四边形的形状是_________．
第15题图
三、解答题（一）：本大题共3小题，第16题10分，第17、18题各7分，共24分．
16．计算：（1）；
（2）．
17．如图，在四边形中，已知，，，，．求证：是直角三角形．
18．我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形，如图，在四边形中，，，，分别是边，，，的中点，依次连接各边中点得到中点四边形，连接，证明：四边形是平行四边形．
四、解答题（二）：本大题3小题，每小题9分，共27分．
19．某校八年级（1）班学生以跨学科主题学习为载体，综合运用体育、数学、生物学等知识，研究体育课的运动负荷．在体育课基本部分运动后，测量统计了部分学生的心率情况，按心率次数（次／分钟），分为如下五组：组：，组：，组：，组：，组：．
根据统计数据绘制了不完整的统计图（如图所示），请结合统计图解答下列问题：
（1）其中组数据为：70，65，65，50，50，60，60，60．组数据的中位数是________次，众数是________次，平均数是________次。
（2）这部分学生共有________人，组频数是________人。
（3）一般运动的适宜心率为（次／分钟），即、组都是适宜的心率。该校共有2000名学生，依据此次跨学科研究结果，估计该校大约有多少名学生达到适宜心率．
20．如图，在四边形中，，，对角线，交于点，平分，过点作，交的延长线于点，连接．
（1）求证：四边形是菱形．
（2）若，，求的长．
21．“五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游。甲乙两公司出租汽车每日所需费用和租车时间成函数关系如图所示，设租车时间为小时，租用甲公司的车每日所需费用为元，租用乙公司的车每日所需费用为元。根据以上信息，解答下列问题：
（1）分别求出，关于x的函数表达式（）；
（2）求出当租车时间为多少时，两公司所需费用相同？直接写出当租车时间范围为多少时，甲公司费用便宜？
五、解答题（三）：本大题2小题，每小题12分，共24分．
22．【阅读与应用】如图1已知平面内两点、，过这两点分别做垂直于轴和轴的虚线相交于点，则间的距离为，则，同理间的距离为，则，由勾股定理得：，即：，则平面内任意两点间的距离公式为．
图l 图2
图3 图4
（1）如图2，已知点、，试利用两点间的距离公式求、两点间的距离？
（2）课本阅读：如果一个三角形的三边长分别为，，，记，那么这个三角形的面积为．这个公式叫“海伦公式”。
如图3，在（1）的条件下，中，，，，试利用“海伦公式”，求的面积？
（3）如图4，在（2）的条件下。过点作，垂足为，求线段的长？
23．【综合探究】
在平面直角坐标系中，点、，点为线段的中点，则线段的中点的坐标为

图l 图2 图3
（1）如图l，已知点、，则线段的中点坐标为_________；
（2）如图2，在（1）的条件下，过点、的直线交轴于点，交轴于点，图中点为轴上的动点，当时，求点的坐标．
（3）如图3，在（1）（2）的条件下，且点在轴的负半轴时，点是轴上的动点，点是直线上的动点，存在以，，，为顶点的四边形为平行四边形，则点的坐标为______________________．