






还剩34页未读,
继续阅读
所属成套资源:全套华东师大版初中数学九年级上册素养测试+综合测试课件
成套系列资料,整套一键下载
华东师大版初中数学九年级上册第23章素养基础测试卷课件
展开
这是一份华东师大版初中数学九年级上册第23章素养基础测试卷课件,共42页。
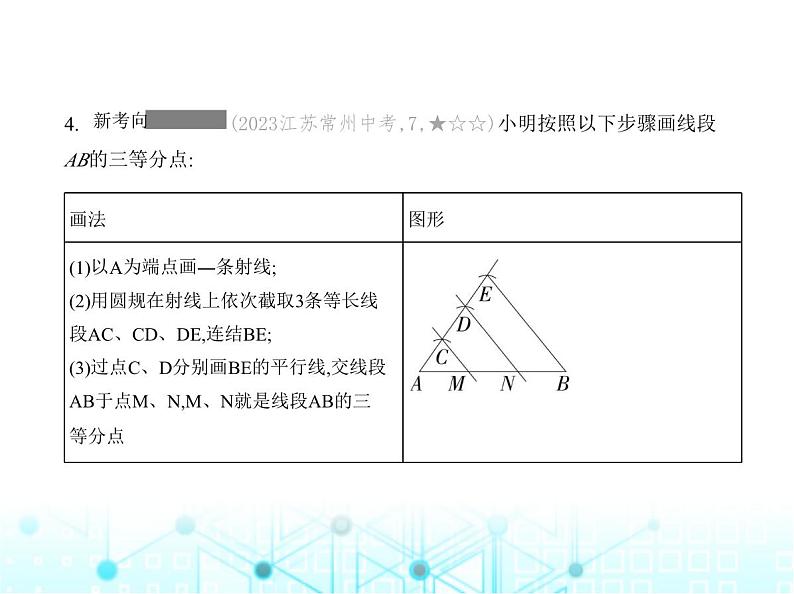
九年级 上册 第23章 素养基础测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2023江苏扬州邗江月考,1,★☆☆)下列图形中,不是相似图形的一组是 对应目标编号M9123001 ( ) D解析 D A.形状相同,但大小不同,符合相似形的定义,故不符合题意;B.形状相 同,但大小不同,符合相似形的定义,故不符合题意;C.形状相同,但大小不同,符合 相似形的定义,故不符合题意;D.形状不相同,不符合相似形的定义,故符合题意. 故选D.2. (新独家原创,★☆☆)在一幅比例尺为1∶10 000 000的东三省地图上,量得哈 尔滨与长春之间的直线距离约为2.4 cm,则哈尔滨、长春两地之间的实际直线 距离大约是 对应目标编号M9123001 ( )A. 24×102 km B. 2.4×103 kmC. 2.4×102 km D. 2.3×102 kmC解析 C 实际直线距离约为2.4×10 000 000 cm=2.4×102 km.3. (2023河南洛阳伊川期末,3,★☆☆)下列各组的四条线段是成比例线段的是 对应目标编号M9123001 ( )A. a=4,b=6,c=5,d=10 B. a=1,b=2,c=3,d=4C. a= ,b=3,c=2,d= D. a=2,b= ,c=2 ,d= D解析 D ∵4×10≠6×5,∴选项A中的四条线段不是成比例线段;∵1×4≠2×3,∴选项B中的四条线段不是成比例线段;∵ ×3≠2× ,∴选项C中的四条线段不是成比例线段;∵2× = ×2 ,∴选项D中的四条线段是成比例线段.4. (2023江苏常州中考,7,★☆☆)小明按照以下步骤画线段 AB的三等分点:这一画图过程体现的数学依据是 对应目标编号M9123002 ( )A. 两直线平行,同位角相等B. 两条平行线之间的距离处处相等C. 垂直于同一条直线的两条直线平行D. 两条直线被一组平行线所截,所得的对应线段成比例D解析 D ∵CM∥DN∥BE,∴AC∶CD∶DE=AM∶MN∶NB,∵AC=CD=DE,∴AM=MN=NB,∴这一画图过程体现的数学依据是两条直线被一组平行线所截,所 得的对应线段成比例.5. (2024河南南阳卧龙一模,8,★☆☆)如图,添加下列条件, 仍不能判定△ADB∽△ABC的是 对应目标编号M9123003 ( ) A. ∠ABD=∠ACB B. ∠ADB=∠ABCC. AB2=AD·AC D. AD·BC=AB·DBD解析 D ∵∠ABD=∠ACB,∠A=∠A,∴△ADB∽△ABC,故选项A不符合题意; ∵∠ADB=∠ABC,∠A=∠A,∴△ADB∽△ABC,故选项B不符合题意;根据AB2= AD·AC可得AB∶AC=AD∶AB,结合∠A=∠A能判定△ADB∽△ABC,故选项C不 符合题意;若添加AD·BC=AB·DB,仍不能判定△ADB∽△ABC,故选项D符合题意.模型解读 相似三角形模型——母子型此模型中的两个三角形有一个“公共角”,只需再找一对等角或证明夹这个公 共角的两边成比例,就可说明这两个三角形相似.6. (2024四川眉山仁寿期末,5,★☆☆)如图,以点O为位似中心,把△ABC的各边放 大为原来的2倍得到△A'B'C',以下说法中错误的是 对应目标编号M9123006( ) A. AO∶AA'=1∶3B. A,O, A'三点在同一条直线上C. S△ABC∶S△A'B'C'=1∶2D. BC∥B'C'C解析 C ∵点O为位似中心,把△ABC的各边放大为原来的2倍得到△A'B'C',∴△ABC∽△A'B'C',BC∥B'C',OA∶OA'=AB∶A'B'=1∶2,A,O,A'三点在同一条直线 上,∴S△ABC∶S△A'B'C'= =1∶4,AO∶AA'=1∶3.故选C.7. (2024吉林长春第二实验中学期中,4,★☆☆)如图,在△ABC中,∠ACD=∠B,若 AD=2,AC= ,则AB的长为( ) A. 5 B. 7 C. 2 D. 2 A8. (2023四川绵阳中考,10,★☆☆)黄金分割由于其美学性质,受到摄影爱好者和 艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理:如图,已知正方形 ABCD,取BC边的中点E,以E为圆心,线段DE的长为半径作圆,与BC边的延长线交 于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形.若CF=4a,则AB = 对应目标编号M9123001 ( ) A. ( -1)a B. (2 -2)a C. ( +1)a D. (2 +2)aD解析 D 设AB=x,∵四边形ABCD是正方形,∴AB=BC=x,∵矩形ABFG是黄金 矩形,∴ = ,∴ = ,解得x=(2+2 )a,经检验,x=(2+2 )a是原方程的根,∴AB=(2+2 )a.9. (2022广东佛山南海外国语学校模拟,7,★☆☆)如图, 已知△ABC的面积为1,连结△ABC三边中点构成第2个三角形,再连结第2个三角 形的三边中点构成第3个三角形,……,以此类推,则第2 021个三角形的面积为 对应目标编号M9123003 ( ) A. B. C. D. C解析 C ∵连结△ABC各边中点构成第2个三角形,∴第2个三角形与△ABC相似,且相似比为1∶2,∴第2个三角形与△ABC的面积比为1∶4,∵△ABC的面积为1,∴第2个三角形的面积为1× = ,同理,第3个三角形的面积为1× × = ,第4个三角形的面积为1× × × = ,∴第n个三角形的面积为 ,故第2 021个三角形的面积为 .10. (2024江苏南京鼓楼期末,6,★★★)如图,将等边三角形纸片ABC折叠,使点A 落在边BC上的D处,MN为折痕.若 = ,则 的值为 ( ) A. B. C. D. C解析 C ∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∴∠BDM+∠BMD=120°,由折叠可知DM=AM,DN=AN,∠MDN=∠A=60°,∴∠BDM+∠CDN=120°,∴∠BMD=∠CDN,∴△BDM∽△CND,∴ = = ,∵ = ,∴可设BD=x,CD=2x,∴BC=AB=AC=3x,设AM=DM=k,∴BM=3x-k,∴ = , = ,∴CN= ,DN= ,∵DN+CN=AN+CN=AC=3x,∴ + =3x,∴k= x,∴DN= = x,∴ = = × = .二、填空题(共6小题,每小题4分,计24分)11. [教材变式P96T9](2023贵州中考,14,★☆☆)如图所示的是贵阳市城市轨道 交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为x轴、y轴的正 方向建立平面直角坐标系,若贵阳北站的坐标是(-2,7),则龙洞堡机场的坐标是 . 对应目标编号M9123007 (9,-4)解析 依题意建立平面直角坐标系如下,点O即为平面直角坐标系原点,则龙洞 堡机场的坐标为(9,-4). 12. (2024陕西西安长安期末,15,★☆☆)已知两个相似三角形的周长比为2∶3,它 们的面积之差为40,那么它们的面积之和为 . 对应目标编号M9123003104解析 ∵两个相似三角形的周长比为2∶3,∴它们的相似比为2∶3,∴它们的面 积比为4∶9,设两个三角形的面积分别为4k,9k,由题意得9k-4k=40,解得k=8,∴两 个三角形的面积分别为32,72,∴它们的面积之和是32+72=104.13. [一题多解](2023吉林长春绿园期末,17,★☆☆)如图所示,已知△ABC,延长 BC到点D,使CD=BC,取AB的中点F,连结FD交AC于点E,则 的值为 . 对应目标编号M9123003 解析 解法1:如图1,连结AD.∵CD=BC,∴点C为BD的中点.又∵点F为AB的中点,AC和DF交于点E,∴点E为△ABD的重心,∴ = .解法2:如图2,连结AD,FC. ∵CD=BC,点F为AB的中点,∴FC是△ABD的中位线,∴ = ,FC∥AD.∴△FEC∽△DEA,∴ = = ,∴EA=2EC,∴ = . 图1 图214. (2024浙江杭州拱墅公益中学月考,14,★☆☆)小明和几位同学做手的影子游 戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为: 可以借助物体的影子长度计算光源到物体的距离.于是,他们做了以下尝试.如 图,垂直于地面放置的正方形框架ABCD,边AB的长为40 cm,在其上方点P处有一 灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为16 cm,那么灯 泡到地面的距离为 cm. 对应目标编号M9123004 140解析 ∵AD∥A'D',∴△PAD∽△PA'D',∴ = ,∴ = ,∴PM=140 cm,∴灯泡到地面的距离为140 cm.15. (2023山东泰安中考,17,★★☆)如图,在△ABC中,AC=BC=16,点D在AB上,点E 在BC上,点B关于直线DE的对称点为点B',连结DB',EB',分别与AC相交于F点,G 点,若AF=8,DF=7,B'F=4,则CG的长度为 . 解析 ∵△BDE与△B'DE关于直线DE对称,∴∠B=∠B'.∵AC=BC,∴∠A=∠B,∴∠A=∠B',又∵∠AFD=∠B'FG,∴△ADF∽ △B'GF,∴ = .∵AF=8,DF=7,B'F=4,∴ = ,∴GF= ,∴CG=AC-AF-GF=16-8- = .16. (2024河南南阳淅川期中,18,★★☆)如图,在矩形ABCD中,E是AD边的中点, BE⊥AC于点F,则下列结论:①△AEF∽△CAB;②BF=2EF;③ = .其中正确结论的个数是 . 3解析 ∵BE⊥AC,∴∠AFE=90°,∴∠CAE+∠AEB=90°,∵四边形ABCD是矩形, ∴∠BAD=90°,∴∠BAC+∠CAE=90°,∴∠BAC=∠AEB,∵∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;∵E是AD边的中点,∴AD=2AE,∵四边形ABCD是矩 形,∴AD=BC,AD∥BC,∴△AFE∽△CFB,∴ = =2,∴BF=2EF,故②正确;∵∠BEA+∠ABE=90°,∠BEA+∠CAD=90°,∴∠ABE=∠CAD,∵∠BAE=∠ADC=90°,∴△BAE∽△ADC,∴ = ,∵AB=DC,∴DC2=AD·AE= ,∴ = ,故③正确.故正确结论的个数为3.三、解答题(共5小题,计56分)17. (2024陕西商洛商南湘河中学期末,16,★☆☆)(8分)如图,直线AD,BC交于点O, AB∥EF∥CD,若AO=2,OF=1,FD=3,求 的值. 对应目标编号M9123002 解析 ∵AO=2,OF=1,FD=3,∴AF=AO+OF=2+1=3,AD=AO+OF+FD=3+3=6,∵AB∥EF∥CD,∴ = = = .18. (2024安徽六安期末16,★☆☆)(10分)如图,在平面直角坐标系中,△ABC的三 个顶点分别为A(-2,1),B(-1,4),C(-3,2).(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出点C1的坐标.(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形 △A2B2C2,并直接写出点C2的坐标. 解析 (1)如图所示,△A1B1C1即为所求,点C1的坐标为(3,2).(2)如图所示,△A2B2C2即为所求,点C2的坐标为(-6,4). 19. (2023山西长治潞城期末,18,★☆☆)(12分)如图,小明画了一个锐角△ABC,并 作出了它的两条高AD和BE,两高相交于点P.图中共有多少对相似三角形?请你 任选一对进行证明. 对应目标编号M9123003 解析 题图中共有6对相似三角形,它们分别是△CBE∽△CAD;△AEP∽△ADC;△BDP∽△BEC;△BDP∽△AEP;△BEC∽△AEP;△BDP∽△ADC.答案不唯一,如选择△BDP∽△AEP:证明:∵BE⊥AC,AD⊥BC,∴∠AEP=∠BDP=90°,又∠APE=∠BPD,∴△BDP∽△AEP.20. (2024山西省实验中学一模,24,★★☆)(12分)为了加强视力保护意识,欢欢想 在书房里挂一张测试距离为5 m的视力表,但两面墙之间的距离只有3 m.在一次 课题学习课上,欢欢向全班同学征集“解决空间过小,如何放置视力表问题”的 方案,其中甲、乙两位同学设计方案新颖,构思巧妙. 对应目标编号M9123004(1)甲同学的方案:如图①,根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应位置 “E”的高度是多少?(2)乙同学的方案:使用平面镜来解决房间小的问题.如图②,若使墙面镜子能呈现 完整的视力表,由平面镜成像原理,作出了光路图,其中视力表AB的上、下边 沿A、B发出的光线经平面镜MM'的上、下边沿反射后射入人眼C.如果视力表的 全长为0.8 m,请计算出平面镜的长. 解析 (1)∵FD∥BC,∴△ADF∽△ABC,∴ = ,∴ = ,∴FD=2.1 cm,故小视力表中相应位置“E”的高度是2.1 cm.(2)如图,作CD⊥MM',垂足为D,延长CD交A'B'于E,∵AB∥MM'∥A'B',∴CE⊥A'B',∴△CMM'∽△CA'B',∴ = ,∵CD=CE-DE=5-3=2(m),CE=5 m,A'B'=AB=0.8 m,∴ = ,∴MM'=0.32 m,∴平面镜的长为0.32 m.21. (2024吉林长春双阳期末,22,★★☆)(14分) 【教材呈现】华师版九年级上册63页例1.如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长. 【应用拓展】(1)如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连结DF,交AC 于点E,若DE∶EF=3∶1,DG∥AC,EC=2,求AC的长.(2)如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连结DE交AC 于点F,若点A为DB的中点,CE∶EB=1∶2,△DBE的面积为4,求△CFE(阴影部分)的面积. 解析 【教材呈现】∵点D是边AB的三等分点,∴ = ,∵DE∥BC,∴△ADE∽△ABC,∴ = = ,∵DE=5,∴BC=15.【应用拓展】(1)∵DE∶EF=3∶1,∴ = ,∵DG∥AC,∴△FEC∽△FDG,∴ = ,即 = ,解得DG=8.∵点D是边AB的中点,DG∥AC,∴DG是△ABC的中位线,∴AC=2DG=16. (2)如图,过点A作AG∥DE,∵点A为DB的中点,∴ = = ,∵CE∶EB=1∶2,∴BG=EG=CE,∵△DBE的面积为4,∴△ABG的面积为1,∴△ACG的面积为2,∴ = ,即 = ,∴△CFE的面积为 .
九年级 上册 第23章 素养基础测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2023江苏扬州邗江月考,1,★☆☆)下列图形中,不是相似图形的一组是 对应目标编号M9123001 ( ) D解析 D A.形状相同,但大小不同,符合相似形的定义,故不符合题意;B.形状相 同,但大小不同,符合相似形的定义,故不符合题意;C.形状相同,但大小不同,符合 相似形的定义,故不符合题意;D.形状不相同,不符合相似形的定义,故符合题意. 故选D.2. (新独家原创,★☆☆)在一幅比例尺为1∶10 000 000的东三省地图上,量得哈 尔滨与长春之间的直线距离约为2.4 cm,则哈尔滨、长春两地之间的实际直线 距离大约是 对应目标编号M9123001 ( )A. 24×102 km B. 2.4×103 kmC. 2.4×102 km D. 2.3×102 kmC解析 C 实际直线距离约为2.4×10 000 000 cm=2.4×102 km.3. (2023河南洛阳伊川期末,3,★☆☆)下列各组的四条线段是成比例线段的是 对应目标编号M9123001 ( )A. a=4,b=6,c=5,d=10 B. a=1,b=2,c=3,d=4C. a= ,b=3,c=2,d= D. a=2,b= ,c=2 ,d= D解析 D ∵4×10≠6×5,∴选项A中的四条线段不是成比例线段;∵1×4≠2×3,∴选项B中的四条线段不是成比例线段;∵ ×3≠2× ,∴选项C中的四条线段不是成比例线段;∵2× = ×2 ,∴选项D中的四条线段是成比例线段.4. (2023江苏常州中考,7,★☆☆)小明按照以下步骤画线段 AB的三等分点:这一画图过程体现的数学依据是 对应目标编号M9123002 ( )A. 两直线平行,同位角相等B. 两条平行线之间的距离处处相等C. 垂直于同一条直线的两条直线平行D. 两条直线被一组平行线所截,所得的对应线段成比例D解析 D ∵CM∥DN∥BE,∴AC∶CD∶DE=AM∶MN∶NB,∵AC=CD=DE,∴AM=MN=NB,∴这一画图过程体现的数学依据是两条直线被一组平行线所截,所 得的对应线段成比例.5. (2024河南南阳卧龙一模,8,★☆☆)如图,添加下列条件, 仍不能判定△ADB∽△ABC的是 对应目标编号M9123003 ( ) A. ∠ABD=∠ACB B. ∠ADB=∠ABCC. AB2=AD·AC D. AD·BC=AB·DBD解析 D ∵∠ABD=∠ACB,∠A=∠A,∴△ADB∽△ABC,故选项A不符合题意; ∵∠ADB=∠ABC,∠A=∠A,∴△ADB∽△ABC,故选项B不符合题意;根据AB2= AD·AC可得AB∶AC=AD∶AB,结合∠A=∠A能判定△ADB∽△ABC,故选项C不 符合题意;若添加AD·BC=AB·DB,仍不能判定△ADB∽△ABC,故选项D符合题意.模型解读 相似三角形模型——母子型此模型中的两个三角形有一个“公共角”,只需再找一对等角或证明夹这个公 共角的两边成比例,就可说明这两个三角形相似.6. (2024四川眉山仁寿期末,5,★☆☆)如图,以点O为位似中心,把△ABC的各边放 大为原来的2倍得到△A'B'C',以下说法中错误的是 对应目标编号M9123006( ) A. AO∶AA'=1∶3B. A,O, A'三点在同一条直线上C. S△ABC∶S△A'B'C'=1∶2D. BC∥B'C'C解析 C ∵点O为位似中心,把△ABC的各边放大为原来的2倍得到△A'B'C',∴△ABC∽△A'B'C',BC∥B'C',OA∶OA'=AB∶A'B'=1∶2,A,O,A'三点在同一条直线 上,∴S△ABC∶S△A'B'C'= =1∶4,AO∶AA'=1∶3.故选C.7. (2024吉林长春第二实验中学期中,4,★☆☆)如图,在△ABC中,∠ACD=∠B,若 AD=2,AC= ,则AB的长为( ) A. 5 B. 7 C. 2 D. 2 A8. (2023四川绵阳中考,10,★☆☆)黄金分割由于其美学性质,受到摄影爱好者和 艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理:如图,已知正方形 ABCD,取BC边的中点E,以E为圆心,线段DE的长为半径作圆,与BC边的延长线交 于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形.若CF=4a,则AB = 对应目标编号M9123001 ( ) A. ( -1)a B. (2 -2)a C. ( +1)a D. (2 +2)aD解析 D 设AB=x,∵四边形ABCD是正方形,∴AB=BC=x,∵矩形ABFG是黄金 矩形,∴ = ,∴ = ,解得x=(2+2 )a,经检验,x=(2+2 )a是原方程的根,∴AB=(2+2 )a.9. (2022广东佛山南海外国语学校模拟,7,★☆☆)如图, 已知△ABC的面积为1,连结△ABC三边中点构成第2个三角形,再连结第2个三角 形的三边中点构成第3个三角形,……,以此类推,则第2 021个三角形的面积为 对应目标编号M9123003 ( ) A. B. C. D. C解析 C ∵连结△ABC各边中点构成第2个三角形,∴第2个三角形与△ABC相似,且相似比为1∶2,∴第2个三角形与△ABC的面积比为1∶4,∵△ABC的面积为1,∴第2个三角形的面积为1× = ,同理,第3个三角形的面积为1× × = ,第4个三角形的面积为1× × × = ,∴第n个三角形的面积为 ,故第2 021个三角形的面积为 .10. (2024江苏南京鼓楼期末,6,★★★)如图,将等边三角形纸片ABC折叠,使点A 落在边BC上的D处,MN为折痕.若 = ,则 的值为 ( ) A. B. C. D. C解析 C ∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∴∠BDM+∠BMD=120°,由折叠可知DM=AM,DN=AN,∠MDN=∠A=60°,∴∠BDM+∠CDN=120°,∴∠BMD=∠CDN,∴△BDM∽△CND,∴ = = ,∵ = ,∴可设BD=x,CD=2x,∴BC=AB=AC=3x,设AM=DM=k,∴BM=3x-k,∴ = , = ,∴CN= ,DN= ,∵DN+CN=AN+CN=AC=3x,∴ + =3x,∴k= x,∴DN= = x,∴ = = × = .二、填空题(共6小题,每小题4分,计24分)11. [教材变式P96T9](2023贵州中考,14,★☆☆)如图所示的是贵阳市城市轨道 交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为x轴、y轴的正 方向建立平面直角坐标系,若贵阳北站的坐标是(-2,7),则龙洞堡机场的坐标是 . 对应目标编号M9123007 (9,-4)解析 依题意建立平面直角坐标系如下,点O即为平面直角坐标系原点,则龙洞 堡机场的坐标为(9,-4). 12. (2024陕西西安长安期末,15,★☆☆)已知两个相似三角形的周长比为2∶3,它 们的面积之差为40,那么它们的面积之和为 . 对应目标编号M9123003104解析 ∵两个相似三角形的周长比为2∶3,∴它们的相似比为2∶3,∴它们的面 积比为4∶9,设两个三角形的面积分别为4k,9k,由题意得9k-4k=40,解得k=8,∴两 个三角形的面积分别为32,72,∴它们的面积之和是32+72=104.13. [一题多解](2023吉林长春绿园期末,17,★☆☆)如图所示,已知△ABC,延长 BC到点D,使CD=BC,取AB的中点F,连结FD交AC于点E,则 的值为 . 对应目标编号M9123003 解析 解法1:如图1,连结AD.∵CD=BC,∴点C为BD的中点.又∵点F为AB的中点,AC和DF交于点E,∴点E为△ABD的重心,∴ = .解法2:如图2,连结AD,FC. ∵CD=BC,点F为AB的中点,∴FC是△ABD的中位线,∴ = ,FC∥AD.∴△FEC∽△DEA,∴ = = ,∴EA=2EC,∴ = . 图1 图214. (2024浙江杭州拱墅公益中学月考,14,★☆☆)小明和几位同学做手的影子游 戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为: 可以借助物体的影子长度计算光源到物体的距离.于是,他们做了以下尝试.如 图,垂直于地面放置的正方形框架ABCD,边AB的长为40 cm,在其上方点P处有一 灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为16 cm,那么灯 泡到地面的距离为 cm. 对应目标编号M9123004 140解析 ∵AD∥A'D',∴△PAD∽△PA'D',∴ = ,∴ = ,∴PM=140 cm,∴灯泡到地面的距离为140 cm.15. (2023山东泰安中考,17,★★☆)如图,在△ABC中,AC=BC=16,点D在AB上,点E 在BC上,点B关于直线DE的对称点为点B',连结DB',EB',分别与AC相交于F点,G 点,若AF=8,DF=7,B'F=4,则CG的长度为 . 解析 ∵△BDE与△B'DE关于直线DE对称,∴∠B=∠B'.∵AC=BC,∴∠A=∠B,∴∠A=∠B',又∵∠AFD=∠B'FG,∴△ADF∽ △B'GF,∴ = .∵AF=8,DF=7,B'F=4,∴ = ,∴GF= ,∴CG=AC-AF-GF=16-8- = .16. (2024河南南阳淅川期中,18,★★☆)如图,在矩形ABCD中,E是AD边的中点, BE⊥AC于点F,则下列结论:①△AEF∽△CAB;②BF=2EF;③ = .其中正确结论的个数是 . 3解析 ∵BE⊥AC,∴∠AFE=90°,∴∠CAE+∠AEB=90°,∵四边形ABCD是矩形, ∴∠BAD=90°,∴∠BAC+∠CAE=90°,∴∠BAC=∠AEB,∵∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;∵E是AD边的中点,∴AD=2AE,∵四边形ABCD是矩 形,∴AD=BC,AD∥BC,∴△AFE∽△CFB,∴ = =2,∴BF=2EF,故②正确;∵∠BEA+∠ABE=90°,∠BEA+∠CAD=90°,∴∠ABE=∠CAD,∵∠BAE=∠ADC=90°,∴△BAE∽△ADC,∴ = ,∵AB=DC,∴DC2=AD·AE= ,∴ = ,故③正确.故正确结论的个数为3.三、解答题(共5小题,计56分)17. (2024陕西商洛商南湘河中学期末,16,★☆☆)(8分)如图,直线AD,BC交于点O, AB∥EF∥CD,若AO=2,OF=1,FD=3,求 的值. 对应目标编号M9123002 解析 ∵AO=2,OF=1,FD=3,∴AF=AO+OF=2+1=3,AD=AO+OF+FD=3+3=6,∵AB∥EF∥CD,∴ = = = .18. (2024安徽六安期末16,★☆☆)(10分)如图,在平面直角坐标系中,△ABC的三 个顶点分别为A(-2,1),B(-1,4),C(-3,2).(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出点C1的坐标.(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形 △A2B2C2,并直接写出点C2的坐标. 解析 (1)如图所示,△A1B1C1即为所求,点C1的坐标为(3,2).(2)如图所示,△A2B2C2即为所求,点C2的坐标为(-6,4). 19. (2023山西长治潞城期末,18,★☆☆)(12分)如图,小明画了一个锐角△ABC,并 作出了它的两条高AD和BE,两高相交于点P.图中共有多少对相似三角形?请你 任选一对进行证明. 对应目标编号M9123003 解析 题图中共有6对相似三角形,它们分别是△CBE∽△CAD;△AEP∽△ADC;△BDP∽△BEC;△BDP∽△AEP;△BEC∽△AEP;△BDP∽△ADC.答案不唯一,如选择△BDP∽△AEP:证明:∵BE⊥AC,AD⊥BC,∴∠AEP=∠BDP=90°,又∠APE=∠BPD,∴△BDP∽△AEP.20. (2024山西省实验中学一模,24,★★☆)(12分)为了加强视力保护意识,欢欢想 在书房里挂一张测试距离为5 m的视力表,但两面墙之间的距离只有3 m.在一次 课题学习课上,欢欢向全班同学征集“解决空间过小,如何放置视力表问题”的 方案,其中甲、乙两位同学设计方案新颖,构思巧妙. 对应目标编号M9123004(1)甲同学的方案:如图①,根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应位置 “E”的高度是多少?(2)乙同学的方案:使用平面镜来解决房间小的问题.如图②,若使墙面镜子能呈现 完整的视力表,由平面镜成像原理,作出了光路图,其中视力表AB的上、下边 沿A、B发出的光线经平面镜MM'的上、下边沿反射后射入人眼C.如果视力表的 全长为0.8 m,请计算出平面镜的长. 解析 (1)∵FD∥BC,∴△ADF∽△ABC,∴ = ,∴ = ,∴FD=2.1 cm,故小视力表中相应位置“E”的高度是2.1 cm.(2)如图,作CD⊥MM',垂足为D,延长CD交A'B'于E,∵AB∥MM'∥A'B',∴CE⊥A'B',∴△CMM'∽△CA'B',∴ = ,∵CD=CE-DE=5-3=2(m),CE=5 m,A'B'=AB=0.8 m,∴ = ,∴MM'=0.32 m,∴平面镜的长为0.32 m.21. (2024吉林长春双阳期末,22,★★☆)(14分) 【教材呈现】华师版九年级上册63页例1.如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长. 【应用拓展】(1)如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连结DF,交AC 于点E,若DE∶EF=3∶1,DG∥AC,EC=2,求AC的长.(2)如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连结DE交AC 于点F,若点A为DB的中点,CE∶EB=1∶2,△DBE的面积为4,求△CFE(阴影部分)的面积. 解析 【教材呈现】∵点D是边AB的三等分点,∴ = ,∵DE∥BC,∴△ADE∽△ABC,∴ = = ,∵DE=5,∴BC=15.【应用拓展】(1)∵DE∶EF=3∶1,∴ = ,∵DG∥AC,∴△FEC∽△FDG,∴ = ,即 = ,解得DG=8.∵点D是边AB的中点,DG∥AC,∴DG是△ABC的中位线,∴AC=2DG=16. (2)如图,过点A作AG∥DE,∵点A为DB的中点,∴ = = ,∵CE∶EB=1∶2,∴BG=EG=CE,∵△DBE的面积为4,∴△ABG的面积为1,∴△ACG的面积为2,∴ = ,即 = ,∴△CFE的面积为 .
相关资料
更多









