






还剩36页未读,
继续阅读
所属成套资源:全套华东师大版初中数学九年级上册素养测试+综合测试课件
成套系列资料,整套一键下载
华东师大版初中数学九年级上册第25章素养基础测试卷课件
展开
这是一份华东师大版初中数学九年级上册第25章素养基础测试卷课件,共44页。
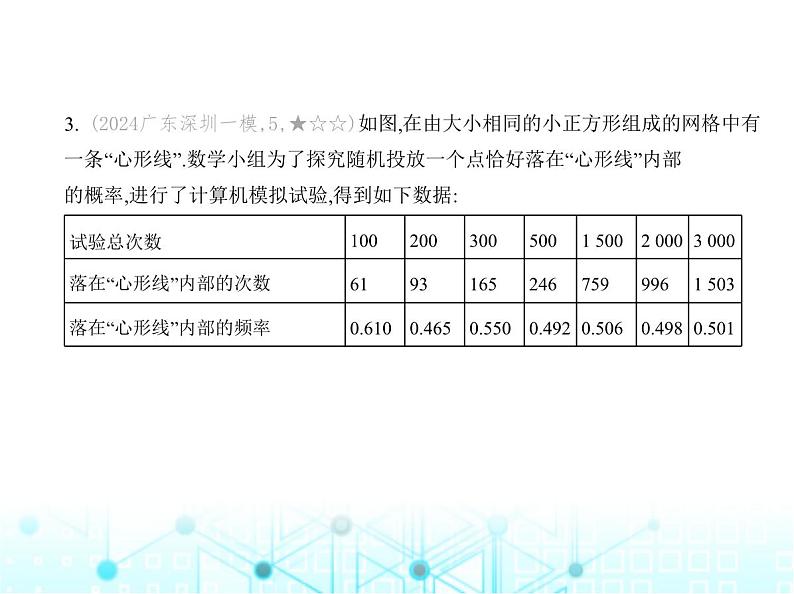
九年级 上册 第25章 素养基础测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2023辽宁盘锦中考,4,★☆☆)下列事件中,是必然事件的是 对应目标编号M9125001 ( )A. 任意画一个三角形,其内角和是180°B. 任意买一张电影票,座位号是单号C. 掷一次骰子,向上一面的点数是3D. 射击运动员射击一次,命中靶心A解析 A 选项B、C、D中的事件均为随机事件,选项A中的事件是必然事件.2. (2023河北承德三中期末,4,★☆☆)某个事件发生的概率是 ,这意味着 对应目标编号M9125003 ( )A. 在两次重复试验中该事件必有一次发生B. 在一次试验中没有发生,下次肯定发生C. 在一次试验中已经发生,下次肯定不发生D. 每次试验中事件发生的可能性是50%D3. (2024广东深圳一模,5,★☆☆)如图,在由大小相同的小正方形组成的网格中有 一条“心形线”.数学小组为了探究随机投放一个点恰好落在“心形线”内部 的概率,进行了计算机模拟试验,得到如下数据:根据表中的数据,估计随机投放一点,落在“心形线”内部的概率为 对应目标编号M9125002 ( ) A. 0.46 B. 0.50 C. 0.55 D. 0.61B解析 B 当试验次数逐渐增多时,落在“心形线”内部的频率稳定在0.50附近, 则估计随机投放一点,落在“心形线”内部的概率为0.50.4. [教材变式P141练习](2024福建泉州泉港期末,7,★☆☆)中国对联,文辞精炼,既 是一种生动的艺术表现形式,又是一种我国优秀的文化遗产,一直为广大人民群 众所喜爱、欣赏.若将回文联的上联“处处飞花飞处处”中的每一个字分别写 在一张卡片上,并从这些卡片中随机抽出一张,则抽到“处”的概率为( ) A. B. C. D. D解析 D “处处飞花飞处处”共有7个字,“处”字共有4个,故P(抽到“处”) = .5. (2022辽宁阜新中考,7,★☆☆)如图所示的是由12个全等的等边三角形组成的 图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是 ( )A. B. C. D. D6. (2023湖南常德中考,4,★☆☆)我市“神十五”航天员张 陆和他的两位战友已于2023年6月4日回到地球家园,“神十六”的三位航天员 已在中国空间站开始值守,空间站的主体结构包括天和核心舱、问天实验舱和 梦天实验舱,假设“神十六”甲、乙、丙三名航天员从核心舱进入问天实验舱 和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选2人各进入一个 实验舱开展科学实验,则甲、乙两人同时被选中的概率为 ( )A. B. C. D. B解析 B 依题意画树状图如下: 由图可知共有6种等可能的情况,其中甲、乙两人同时被选中的情况有2种,故 甲、乙两人同时被选中的概率为 = .7. (2023四川德阳中考,5,★☆☆)在6,7,8,9四个数字中任意选取两个数字,则这两 个数字之和为奇数的概率是 对应目标编号M9125003 ( )A. B. C. D. C解析 C 依题意画树状图如下: 由图可知共有12种等可能的结果,其中这两个数字之和为奇数的结果有8种,故 这两个数字之和为奇数的概率为 = .8. (2024四川成都郫都期末,13,★☆☆)如图,已知△ADE、△ABC和3张都标注 一个条件的卡片①②③.从这3张卡片中随机一次性抽取2张,根据这2张的条件, 能判定△ADE∽△ABC的概率为( ) A. B. C. D. B解析 B 若∠1=∠2,∠D=∠B,则△ADE∽△ABC;若∠1=∠2, = ,则△ADE∽△ABC;若∠D=∠B, = ,则无法判定△ADE∽△ABC,故从这3张卡片中随机一次性抽取2张有3种等可能的结果,其中能判定△ADE∽△ABC的结 果有2种,∴能判定△ADE∽△ABC的概率为 .9. (2022山西太原模拟,6,★★☆)孟德尔被誉为现代遗传学之父, 他通过豌豆杂交实验,发现了遗传学的基本规律.如图,纯种高茎豌豆和纯种矮茎 豌豆杂交,子一代都是高茎豌豆,将子一代种子种下去,自花传粉,获得的子二代 豌豆由DD、Dd、dd三种遗传因子控制.由此可知,子二代豌豆中含遗传因子D的 概率是 对应目标编号M9125003 ( ) A. B. C. D. D解析 D 纯种高茎豌豆(DD)和纯种矮茎豌豆(dd)杂交,子一代都是高茎豌豆 (Dd),子一代种子种下去,自花传粉,获得的子二代豌豆由DD、Dd、dd三种遗传 因子控制,比例为1∶2∶1,由此可知,子二代豌豆中含遗传因子D的概率是 .故选D.10. (2024浙江杭州市建兰中学月考,6,★★☆)如图,转盘的红、黄、蓝、紫四个 扇形区域的圆心角分别记为α、β、γ、θ,自由转动转盘,则下列说法错误的是 ( ) A. 若α>90°,则指针落在红色区域的概率大于0.25B. 若α>β+γ+θ,则指针落在红色区域的概率大于落在黄色区域的概率C. 若α-β=γ-θ,则指针落在红色和蓝色区域的概率和为0.5D. 若γ+θ=200°,则指针落在红色和黄色区域的概率和小于0.5C解析 C ∵α>90°,∴ > =0.25,故A中说法正确,不符合题意;∵α>β+γ+θ,∴ > ,故B中说法正确,不符合题意;∵α-β=γ-θ,∴α+θ=β+γ,∵α+β+γ+θ=360°,∴α+θ=β+γ=180°,∵ =0.5,∴指针落在红色和紫色区域的概率和为0.5,故C中说法错误,符合题意;∵γ+θ=200°,α+β+γ+θ=360°,∴α+β=160°,∵ <0.5,∴指针落在红色和黄色区域的概率和小于0.5,故D中说法正确,不符合题意.二、填空题(共6小题,每小题4分,计24分)11. (新独家原创,★☆☆)“若有战,召必回”彰显了退役军人的担当和奉献.某部 队共有50名现役军人将要退役,其中女兵有20名,男兵有30名,若从中随机抽取一 人,恰好抽到男兵的概率是 .12. (2023四川眉山仁寿期末,13,★☆☆)如图所示的是一个被分成6等份的扇形 转盘,小明转了2次指针都停留在红色区域,小明第3次转动指针停留在红色区域 的概率是 . 对应目标编号M9125003 解析 因为转盘被分成6等份,而红色区域占2份,所以P(指针停留在红色区域)= = .易错警示 本题易受前两次转动结果的影响,而误认为第3次转动转盘,指针仍会落在 红色区域.13. (2022四川南充中考,12,★☆☆)老师为帮助学生正确理解物 理变化与化学变化,将6种生活现象制成看上去无差别的卡片(如图).从中随机抽 取一张卡片,抽中的生活现象是物理变化的概率是 . 对应目标编号M9125003 解析 从中随机抽取一张卡片共有6种等可能的结果,抽中的生活现象是物理变 化的结果有2种,所以从中随机抽取一张卡片,抽中的生活现象是物理变化的概 率为 = .14. (2024河南漯河郾城期末,13,★☆☆)我市在某展览馆举办美丽乡村成果展,该 展览馆出入口示意图如图所示,小颖从A入口进,E出口出的概率是 . 对应目标编号M9125003 解析 依题意画树状图如下, 由图可知共有6种等可能的结果,其中小颖从A入口进,E出口出的结果有1种,∴小颖从A入口进,E出口出的概率为 .15. (2024重庆北碚期末,12,★★☆)在一个布袋里装着标号分别为1,2,3 的3个小球,它们除标号外无其他区别,从布袋中随机摸出一个小球后不放回,将 小球上的数字记为a,摇匀,再随机摸出一个小球,将小球上的数字记为b,则a、b使 二次根式 的值为有理数的概率是 . 对应目标编号M9125003解析 本题将概率与二次根式融合,设计新颖巧妙.依题意画树状图如下, 由图可知共有6种等可能的结果,其中a、b使二次根式 的值为有理数的结果有2种,∴a、b使二次根式 的值为有理数的概率为 = .方法解读 注意题目中所给条件(是否放回),若放回,则两次可能出现同一种情况;若不 放回,则两次不可能出现同一种情况.16. (2024河南开封通许期末,17,★★☆)如图,在方格纸中,每个小正方形的边长 均为1,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.先从 D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以取得的 三个点为顶点画三角形,则所画三角形与△ABC面积相等的概率为 . 解析 从D、E两个点中任意取一个点,再从F、G、H三个点中任意取两个不同 的点,画三角形共有6种等可能的结果,分别为△DHF,△DHG,△DFG,△EHF,△EHG,△EFG,由方格可求出S△DHF= ×3×1= ,S△DHG= ×3×4=6,S△DFG= ×3×4=6,S△EHF=16- -6-6= ,S△EHG= ×4×4=8,S△EFG= ×3×4=6,S△ABC= ×3×4=6,因此这6个三角形中与△ABC面积相等的有3个,故所画三角形与△ABC面积相等的概率为 = .三、解答题(共5小题,计56分)17. (2024河南驻马店二中期末,21,★☆☆)(8分)一个袋子中有形状、大小完全相 同的5个红球和3个白球.(1)求从袋子中任意摸出一球恰好是白球的可能性大小.(2)在袋子中再放入n个白球,这些白球与袋子中的小球形状、大小完全相同.从 中任意摸出一球,恰好是红球的可能性是 ,求n的值.解析 (1)∵袋子中有形状、大小完全相同的5个红球和3个白球,∴从袋子中任 意摸出一球恰好是白球的可能性为 = .(2)根据题意得 = ,解得n=2,经检验,n=2是原方程的解,所以n的值为2.18. (2024广东惠州惠阳黄埔学校期末,20,★☆☆)(10分)如图所示的是可以自由 转动的三个转盘,请根据下列情形回答问题:(1)转动转盘①,当转盘停止转动时,指针落在红色区域的概率是 .(2)转动转盘②,当转盘停止转动时,指针落在红色区域的概率是 .(3)请设计转盘③:转盘③已被分成了9个相同的扇形,转动转盘③,当转盘停止转 动时,指针落在白色区域的概率为 ,落在红色区域的概率为 ,落在黄色区域的概率为 .(注:无需涂色,在扇形中填写“红”“白”“黄”即可) 解析 (1)红色区域的圆心角度数为120°,当转盘停止转动时,指针落在红色区域 的概率是 = .(2)红色区域的圆心角度数为360°-(90°+110°)=160°,当转盘停止转动时,指针落在 红色区域的概率是 = .(3)∵转盘③被分成了9个相同的扇形,∴转盘中白色区域的扇形个数为9× =4,红色区域的扇形个数为9× =3,黄色区域的扇形个数为9× =2,∴设计转盘如图所示.(各颜色区域扇形个数满足即可,位置不唯一) 19. (2023辽宁铁岭昌图期末,24,★☆☆)(12分)如图,将一个封闭的圆形装置内部 划分为三个区域,其中A、B两个区域为圆环,C区域为小圆. 对应目标编号M9125003(1)求出A、B、C三个区域的面积.(2)若随机往装置内扔一粒黄豆,求黄豆落在B区域的概率. 解析 (1)SA区域=π×(92-62)=45π(cm2),SB区域=π×(62-32)=27π(cm2),SC区域=π×32=9π(cm2).(2)黄豆落在B区域的概率为 = .20. (2024福建泉州鲤城期末,22,★★☆)(12分)一个不透明的纸箱里有三张完全 相同的卡片,它们上面分别写着 、 、 ,小丽从中抽取一张,记下数后,把卡片放回,搅匀,然后小明再从中抽取一张. 对应目标编号M9125003(1)直接写出小丽抽取的卡片恰好写着 的概率.(2)同学小颖帮他们设计了一个游戏规则:若两人抽取的卡片上的数字之积为有 理数,则小丽获胜;否则小明获胜.你认为这个游戏规则公平吗?若不公平,则对谁 有利?请说明理由.解析 (1)∵有三张完全相同的卡片,写着 的卡片有1张,∴小丽抽取的卡片恰好写着 的概率为 .(2)这个游戏规则不公平,对小丽有利.理由:列表如下,由表格可知共有9种等可能的结果,其中两人抽取的卡片上的数字之积是有理数 的结果有5种,∴P(小丽胜)= ,∴P(小明胜)= ,∵ > ,∴这个游戏规则不公平,对小丽有利.方法解读 保证游戏规则公平的两种途径(1)使参与游戏各方获胜的概率相同;(2)参与游戏的各方获胜的概率虽然不同,但 可以通过分值控制,使各方获胜的概率与分值的积相等.21. (2023山东枣庄中考,20,★★☆)(14分)《义务教育课程方案》和《义务教育 劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学的一门独立课程, 日常生活劳动设定四个任务群:A清洁与卫生,B整理与收纳,C家用器具使用与维 护,D烹饪与营养.学校为了较好地开设课程,对学生最喜欢的任务群进行了调查, 并将调查结果绘制成如图所示的两幅不完整的统计图.请根据统计图解答下列 问题: 对应目标编号M9125003(1)本次调查中,一共调查了 名学生,其中选择“C家用器具使用与维 护”的女生有 名,“D烹饪与营养”的男生有 名.(2)补全条形统计图和扇形统计图.(3)学校想从选择“C家用器具使用与维护”的学生中随机选取两名学生作为 “家居博览会”的志愿者,请用画树状图法或列表法求出所选的学生恰好是一 名男生和一名女生的概率. 解析 (1)3÷15%=20(名),所以本次调查中,一共调查了20名学生,其中选择“C家 用器具使用与维护”的女生人数为20×25%-3=2,选择“D烹饪与营养”的男生 人数为20-3-10-5-1=1.(2)选择“D烹饪与营养”的人数所占的百分比为 ×100%=10%,补全条形统计图和扇形统计图如下:(3)依题意画树状图如下,由图可知共有20种等可能的结果,其中所选的学生恰好 是一名男生和一名女生的结果数为12,故所选的学生恰好是一名男生和一名女 生的概率= = .
九年级 上册 第25章 素养基础测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2023辽宁盘锦中考,4,★☆☆)下列事件中,是必然事件的是 对应目标编号M9125001 ( )A. 任意画一个三角形,其内角和是180°B. 任意买一张电影票,座位号是单号C. 掷一次骰子,向上一面的点数是3D. 射击运动员射击一次,命中靶心A解析 A 选项B、C、D中的事件均为随机事件,选项A中的事件是必然事件.2. (2023河北承德三中期末,4,★☆☆)某个事件发生的概率是 ,这意味着 对应目标编号M9125003 ( )A. 在两次重复试验中该事件必有一次发生B. 在一次试验中没有发生,下次肯定发生C. 在一次试验中已经发生,下次肯定不发生D. 每次试验中事件发生的可能性是50%D3. (2024广东深圳一模,5,★☆☆)如图,在由大小相同的小正方形组成的网格中有 一条“心形线”.数学小组为了探究随机投放一个点恰好落在“心形线”内部 的概率,进行了计算机模拟试验,得到如下数据:根据表中的数据,估计随机投放一点,落在“心形线”内部的概率为 对应目标编号M9125002 ( ) A. 0.46 B. 0.50 C. 0.55 D. 0.61B解析 B 当试验次数逐渐增多时,落在“心形线”内部的频率稳定在0.50附近, 则估计随机投放一点,落在“心形线”内部的概率为0.50.4. [教材变式P141练习](2024福建泉州泉港期末,7,★☆☆)中国对联,文辞精炼,既 是一种生动的艺术表现形式,又是一种我国优秀的文化遗产,一直为广大人民群 众所喜爱、欣赏.若将回文联的上联“处处飞花飞处处”中的每一个字分别写 在一张卡片上,并从这些卡片中随机抽出一张,则抽到“处”的概率为( ) A. B. C. D. D解析 D “处处飞花飞处处”共有7个字,“处”字共有4个,故P(抽到“处”) = .5. (2022辽宁阜新中考,7,★☆☆)如图所示的是由12个全等的等边三角形组成的 图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是 ( )A. B. C. D. D6. (2023湖南常德中考,4,★☆☆)我市“神十五”航天员张 陆和他的两位战友已于2023年6月4日回到地球家园,“神十六”的三位航天员 已在中国空间站开始值守,空间站的主体结构包括天和核心舱、问天实验舱和 梦天实验舱,假设“神十六”甲、乙、丙三名航天员从核心舱进入问天实验舱 和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选2人各进入一个 实验舱开展科学实验,则甲、乙两人同时被选中的概率为 ( )A. B. C. D. B解析 B 依题意画树状图如下: 由图可知共有6种等可能的情况,其中甲、乙两人同时被选中的情况有2种,故 甲、乙两人同时被选中的概率为 = .7. (2023四川德阳中考,5,★☆☆)在6,7,8,9四个数字中任意选取两个数字,则这两 个数字之和为奇数的概率是 对应目标编号M9125003 ( )A. B. C. D. C解析 C 依题意画树状图如下: 由图可知共有12种等可能的结果,其中这两个数字之和为奇数的结果有8种,故 这两个数字之和为奇数的概率为 = .8. (2024四川成都郫都期末,13,★☆☆)如图,已知△ADE、△ABC和3张都标注 一个条件的卡片①②③.从这3张卡片中随机一次性抽取2张,根据这2张的条件, 能判定△ADE∽△ABC的概率为( ) A. B. C. D. B解析 B 若∠1=∠2,∠D=∠B,则△ADE∽△ABC;若∠1=∠2, = ,则△ADE∽△ABC;若∠D=∠B, = ,则无法判定△ADE∽△ABC,故从这3张卡片中随机一次性抽取2张有3种等可能的结果,其中能判定△ADE∽△ABC的结 果有2种,∴能判定△ADE∽△ABC的概率为 .9. (2022山西太原模拟,6,★★☆)孟德尔被誉为现代遗传学之父, 他通过豌豆杂交实验,发现了遗传学的基本规律.如图,纯种高茎豌豆和纯种矮茎 豌豆杂交,子一代都是高茎豌豆,将子一代种子种下去,自花传粉,获得的子二代 豌豆由DD、Dd、dd三种遗传因子控制.由此可知,子二代豌豆中含遗传因子D的 概率是 对应目标编号M9125003 ( ) A. B. C. D. D解析 D 纯种高茎豌豆(DD)和纯种矮茎豌豆(dd)杂交,子一代都是高茎豌豆 (Dd),子一代种子种下去,自花传粉,获得的子二代豌豆由DD、Dd、dd三种遗传 因子控制,比例为1∶2∶1,由此可知,子二代豌豆中含遗传因子D的概率是 .故选D.10. (2024浙江杭州市建兰中学月考,6,★★☆)如图,转盘的红、黄、蓝、紫四个 扇形区域的圆心角分别记为α、β、γ、θ,自由转动转盘,则下列说法错误的是 ( ) A. 若α>90°,则指针落在红色区域的概率大于0.25B. 若α>β+γ+θ,则指针落在红色区域的概率大于落在黄色区域的概率C. 若α-β=γ-θ,则指针落在红色和蓝色区域的概率和为0.5D. 若γ+θ=200°,则指针落在红色和黄色区域的概率和小于0.5C解析 C ∵α>90°,∴ > =0.25,故A中说法正确,不符合题意;∵α>β+γ+θ,∴ > ,故B中说法正确,不符合题意;∵α-β=γ-θ,∴α+θ=β+γ,∵α+β+γ+θ=360°,∴α+θ=β+γ=180°,∵ =0.5,∴指针落在红色和紫色区域的概率和为0.5,故C中说法错误,符合题意;∵γ+θ=200°,α+β+γ+θ=360°,∴α+β=160°,∵ <0.5,∴指针落在红色和黄色区域的概率和小于0.5,故D中说法正确,不符合题意.二、填空题(共6小题,每小题4分,计24分)11. (新独家原创,★☆☆)“若有战,召必回”彰显了退役军人的担当和奉献.某部 队共有50名现役军人将要退役,其中女兵有20名,男兵有30名,若从中随机抽取一 人,恰好抽到男兵的概率是 .12. (2023四川眉山仁寿期末,13,★☆☆)如图所示的是一个被分成6等份的扇形 转盘,小明转了2次指针都停留在红色区域,小明第3次转动指针停留在红色区域 的概率是 . 对应目标编号M9125003 解析 因为转盘被分成6等份,而红色区域占2份,所以P(指针停留在红色区域)= = .易错警示 本题易受前两次转动结果的影响,而误认为第3次转动转盘,指针仍会落在 红色区域.13. (2022四川南充中考,12,★☆☆)老师为帮助学生正确理解物 理变化与化学变化,将6种生活现象制成看上去无差别的卡片(如图).从中随机抽 取一张卡片,抽中的生活现象是物理变化的概率是 . 对应目标编号M9125003 解析 从中随机抽取一张卡片共有6种等可能的结果,抽中的生活现象是物理变 化的结果有2种,所以从中随机抽取一张卡片,抽中的生活现象是物理变化的概 率为 = .14. (2024河南漯河郾城期末,13,★☆☆)我市在某展览馆举办美丽乡村成果展,该 展览馆出入口示意图如图所示,小颖从A入口进,E出口出的概率是 . 对应目标编号M9125003 解析 依题意画树状图如下, 由图可知共有6种等可能的结果,其中小颖从A入口进,E出口出的结果有1种,∴小颖从A入口进,E出口出的概率为 .15. (2024重庆北碚期末,12,★★☆)在一个布袋里装着标号分别为1,2,3 的3个小球,它们除标号外无其他区别,从布袋中随机摸出一个小球后不放回,将 小球上的数字记为a,摇匀,再随机摸出一个小球,将小球上的数字记为b,则a、b使 二次根式 的值为有理数的概率是 . 对应目标编号M9125003解析 本题将概率与二次根式融合,设计新颖巧妙.依题意画树状图如下, 由图可知共有6种等可能的结果,其中a、b使二次根式 的值为有理数的结果有2种,∴a、b使二次根式 的值为有理数的概率为 = .方法解读 注意题目中所给条件(是否放回),若放回,则两次可能出现同一种情况;若不 放回,则两次不可能出现同一种情况.16. (2024河南开封通许期末,17,★★☆)如图,在方格纸中,每个小正方形的边长 均为1,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.先从 D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以取得的 三个点为顶点画三角形,则所画三角形与△ABC面积相等的概率为 . 解析 从D、E两个点中任意取一个点,再从F、G、H三个点中任意取两个不同 的点,画三角形共有6种等可能的结果,分别为△DHF,△DHG,△DFG,△EHF,△EHG,△EFG,由方格可求出S△DHF= ×3×1= ,S△DHG= ×3×4=6,S△DFG= ×3×4=6,S△EHF=16- -6-6= ,S△EHG= ×4×4=8,S△EFG= ×3×4=6,S△ABC= ×3×4=6,因此这6个三角形中与△ABC面积相等的有3个,故所画三角形与△ABC面积相等的概率为 = .三、解答题(共5小题,计56分)17. (2024河南驻马店二中期末,21,★☆☆)(8分)一个袋子中有形状、大小完全相 同的5个红球和3个白球.(1)求从袋子中任意摸出一球恰好是白球的可能性大小.(2)在袋子中再放入n个白球,这些白球与袋子中的小球形状、大小完全相同.从 中任意摸出一球,恰好是红球的可能性是 ,求n的值.解析 (1)∵袋子中有形状、大小完全相同的5个红球和3个白球,∴从袋子中任 意摸出一球恰好是白球的可能性为 = .(2)根据题意得 = ,解得n=2,经检验,n=2是原方程的解,所以n的值为2.18. (2024广东惠州惠阳黄埔学校期末,20,★☆☆)(10分)如图所示的是可以自由 转动的三个转盘,请根据下列情形回答问题:(1)转动转盘①,当转盘停止转动时,指针落在红色区域的概率是 .(2)转动转盘②,当转盘停止转动时,指针落在红色区域的概率是 .(3)请设计转盘③:转盘③已被分成了9个相同的扇形,转动转盘③,当转盘停止转 动时,指针落在白色区域的概率为 ,落在红色区域的概率为 ,落在黄色区域的概率为 .(注:无需涂色,在扇形中填写“红”“白”“黄”即可) 解析 (1)红色区域的圆心角度数为120°,当转盘停止转动时,指针落在红色区域 的概率是 = .(2)红色区域的圆心角度数为360°-(90°+110°)=160°,当转盘停止转动时,指针落在 红色区域的概率是 = .(3)∵转盘③被分成了9个相同的扇形,∴转盘中白色区域的扇形个数为9× =4,红色区域的扇形个数为9× =3,黄色区域的扇形个数为9× =2,∴设计转盘如图所示.(各颜色区域扇形个数满足即可,位置不唯一) 19. (2023辽宁铁岭昌图期末,24,★☆☆)(12分)如图,将一个封闭的圆形装置内部 划分为三个区域,其中A、B两个区域为圆环,C区域为小圆. 对应目标编号M9125003(1)求出A、B、C三个区域的面积.(2)若随机往装置内扔一粒黄豆,求黄豆落在B区域的概率. 解析 (1)SA区域=π×(92-62)=45π(cm2),SB区域=π×(62-32)=27π(cm2),SC区域=π×32=9π(cm2).(2)黄豆落在B区域的概率为 = .20. (2024福建泉州鲤城期末,22,★★☆)(12分)一个不透明的纸箱里有三张完全 相同的卡片,它们上面分别写着 、 、 ,小丽从中抽取一张,记下数后,把卡片放回,搅匀,然后小明再从中抽取一张. 对应目标编号M9125003(1)直接写出小丽抽取的卡片恰好写着 的概率.(2)同学小颖帮他们设计了一个游戏规则:若两人抽取的卡片上的数字之积为有 理数,则小丽获胜;否则小明获胜.你认为这个游戏规则公平吗?若不公平,则对谁 有利?请说明理由.解析 (1)∵有三张完全相同的卡片,写着 的卡片有1张,∴小丽抽取的卡片恰好写着 的概率为 .(2)这个游戏规则不公平,对小丽有利.理由:列表如下,由表格可知共有9种等可能的结果,其中两人抽取的卡片上的数字之积是有理数 的结果有5种,∴P(小丽胜)= ,∴P(小明胜)= ,∵ > ,∴这个游戏规则不公平,对小丽有利.方法解读 保证游戏规则公平的两种途径(1)使参与游戏各方获胜的概率相同;(2)参与游戏的各方获胜的概率虽然不同,但 可以通过分值控制,使各方获胜的概率与分值的积相等.21. (2023山东枣庄中考,20,★★☆)(14分)《义务教育课程方案》和《义务教育 劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学的一门独立课程, 日常生活劳动设定四个任务群:A清洁与卫生,B整理与收纳,C家用器具使用与维 护,D烹饪与营养.学校为了较好地开设课程,对学生最喜欢的任务群进行了调查, 并将调查结果绘制成如图所示的两幅不完整的统计图.请根据统计图解答下列 问题: 对应目标编号M9125003(1)本次调查中,一共调查了 名学生,其中选择“C家用器具使用与维 护”的女生有 名,“D烹饪与营养”的男生有 名.(2)补全条形统计图和扇形统计图.(3)学校想从选择“C家用器具使用与维护”的学生中随机选取两名学生作为 “家居博览会”的志愿者,请用画树状图法或列表法求出所选的学生恰好是一 名男生和一名女生的概率. 解析 (1)3÷15%=20(名),所以本次调查中,一共调查了20名学生,其中选择“C家 用器具使用与维护”的女生人数为20×25%-3=2,选择“D烹饪与营养”的男生 人数为20-3-10-5-1=1.(2)选择“D烹饪与营养”的人数所占的百分比为 ×100%=10%,补全条形统计图和扇形统计图如下:(3)依题意画树状图如下,由图可知共有20种等可能的结果,其中所选的学生恰好 是一名男生和一名女生的结果数为12,故所选的学生恰好是一名男生和一名女 生的概率= = .
相关资料
更多









