华东师大版初中数学九年级上册专项素养巩固训练卷(八)化斜为直解三角形的常见类型练课件

这是一份华东师大版初中数学九年级上册专项素养巩固训练卷(八)化斜为直解三角形的常见类型练课件，共12页。
专项素养巩固训练卷(八)　化斜为直解三角形的常见类型(练模型)
类型一　分割构造直角三角形(一)背靠背型
1. (2023西藏中考,25,★☆☆)如图,轮船甲和轮船乙同时离开海港O,轮船甲沿北 偏东60°方向航行,轮船乙沿东南方向航行,2小时后,轮船甲到达A处,轮船乙到达 B处,此时轮船甲正好在轮船乙的正北方向.已知轮船甲的速度为每小时25海里, 求轮船乙的速度.(结果保留根号)    对应目标编号M9124006 
解析　如图,过O作OD⊥AB于D,在Rt△AOD中,∠AOD=90°-60°=30°,OA=25×2=50(海里),∴OD=OA·cs 30°=50× =25 (海里),在Rt△ODB中,∠DOB=45°,∴OB= OD=25 × =25 (海里),∴轮船乙的速度为  海里/小时.
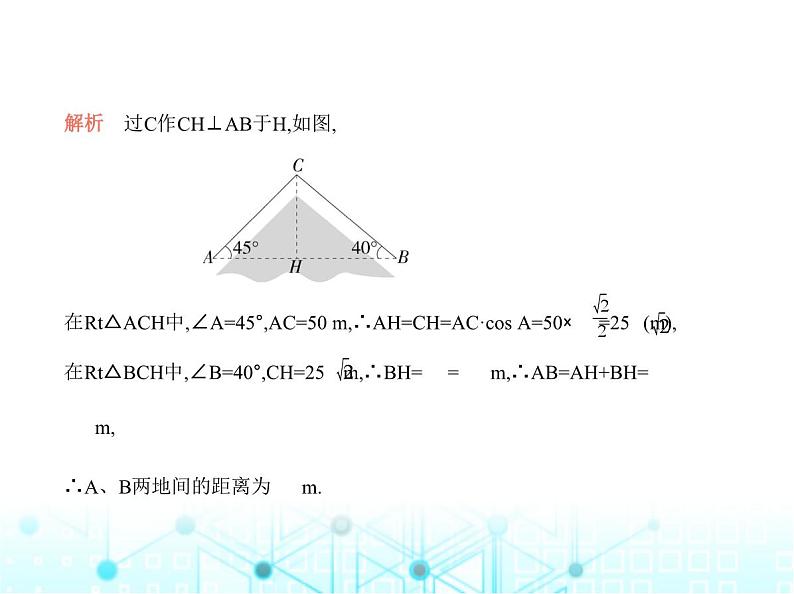
2. (2023内蒙古呼和浩特中考,18,★☆☆)如图所示,小明上学途中要经过A,B两 地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB.小明想知道A,B两地 间的距离,测得AC=50 m,∠A=45°,∠B=40°,请帮小明求出A、B两地间的距离. (结果用含非特殊角的三角函数和根式表示即可) 
解析　过C作CH⊥AB于H,如图,在Rt△ACH中,∠A=45°,AC=50 m,∴AH=CH=AC·cs A=50× =25 (m),在Rt△BCH中,∠B=40°,CH=25  m,∴BH= =  m,∴AB=AH+BH= m,∴A、B两地间的距离为 m.
3. (2023湖南张家界中考,20,★☆☆)“游张家界山水,逛七十二奇楼”成为今年 旅游新特色.某数学兴趣小组用无人机测量奇楼AB的高度,测量方案如图,先将 无人机垂直上升至距水平地面225 m的P点,测得奇楼顶端A的俯角为15°,再将无 人机沿水平方向飞行200 m到达点Q,测得奇楼底端B的俯角为45°,求奇楼AB的 高度.(结果精确到1 m,参考数据:sin 15°≈0.26,cs 15°≈0.97,tan 15°≈0.27)    对应目标编号M9124006 
解析　如图,延长BA交PQ的延长线于C,则∠ACQ=90°,由题意得BC=225 m,PQ=200 m,在Rt△BCQ中,∠BQC=45°,∴CQ=BC=225 m,∴ PC=PQ+CQ=425 m,在Rt△PCA中,∴AC=tan ∠APC·PC≈0.27×425=114.75(m), ∴AB=BC-AC=225-114.75=110.25≈110(m),故奇楼AB的高度约为110 m.
4. (2024山东青岛二模,18,★★☆)为了响应国家“双减”政策,适当改变作业的 方式,某校内数学兴趣小组组织了一次测量探究活动.如图,大楼的顶部竖有一块 广告牌CD,同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB 向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶ ,AB=12米,AE=27米,求广告牌CD的高度. 测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.41, ≈1.73,sin 53°≈ ,cs 53°≈ ,tan 53° ≈   
解析　如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M,N, ∵i=1∶ = = =tan∠BAM,∴∠BAM=30°,∴AM= AB=6 米,∴ME=AM+AE=(6 +27)米,∵∠CBN=45°,∴CN=BN=ME=(6 +27)米,∴CE=CN+NE=(6 +33)米,在Rt△ADE中,∠DAE=53°,AE=27米,∴DE=AE·tan 53°≈27× =36(米),∴CD=CE-DE=6 +33-36=6 -3≈10.38-3≈7.4(米),故广告牌CD的高约为7.4米.
类型二　填补构造直角三角形
5. (2023陕西师大附中期末,23,★★☆)如图,小明家对面有一个山坡,一根电线杆 PQ直立在山坡上,小明想用学过的数学知识测量电线杆的高度,设计了如下方 案:小明在家门口小广场点A处,利用测倾器测得电线杆顶端点P的仰角∠PCE=45°,从点A朝着CE方向走8米到达B点,测得电线杆顶端点P的仰角∠PDE=60°,电 线杆底端点Q的仰角∠QDE=30°,计算电线杆PQ的高度(已知:测倾器的高度AC= BD,AC⊥AB,BD⊥AB,PQ⊥AB,结果保留根号).