华师大版九年级上册24.4 解直角三角形图片ppt课件

这是一份华师大版九年级上册24.4 解直角三角形图片ppt课件，共27页。

专项素养综合全练（八）
解直角三角形中的五种思想方法
1.(2024河南南阳实验学校月考)在平面直角坐标系中,直线y =3x与x轴的夹角为α,求α的正弦值和余弦值.
解析　如图,在直线y=3x上任取一点P(不与点O重合),过点P 作PA⊥x轴于点A.设点P的横坐标为a(a≠0),则点P的纵坐标 为3a,所以在Rt△PAO中,OA=|a|,AP=3|a|,由勾股定理得OP=  = |a|,∴sin α= = = ,cs α= = = . 
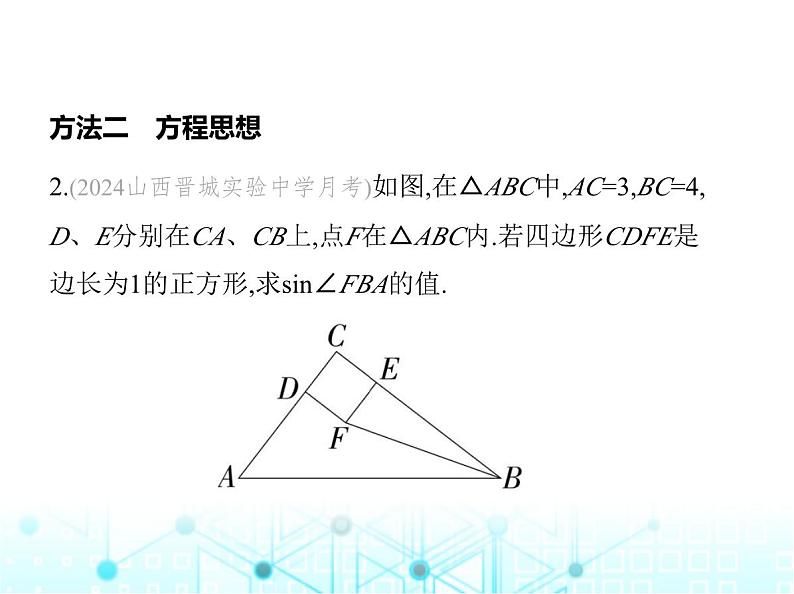
2.(2024山西晋城实验中学月考)如图,在△ABC中,AC=3,BC=4,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是 边长为1的正方形,求sin∠FBA的值. 
解析　如图,连结AF,过点F作FG⊥AB于G,∵四边形CDFE是 边长为1的正方形,∴CD=CE=DF=EF=1,∠C=∠ADF=90°,∵ AC=3,BC=4,∴AD=2,BE=3,AB= =5,∴AF= = ,BF= = ,设BG=x,则AG=5-x,∵FG2=AF2-AG2=BF2-BG2,∴5-(5-x)2=10-x2,解得x=3,∴FG=  =1,∴sin∠FBA= = = .
3.(2023湖南娄底中考)几位同学在老师的指导下到某景区进 行户外实践活动,在登山途中发现该景区某两座山之间风景 优美,但路陡难行,为了便于建议景区管理处在这两山顶间建 观光索道,他们分别在两山顶上取A、B两点,并过点B架设一 水平线型轨道CD(如图所示),使得∠ABC=α,从点B出发沿CD 方向前进20米到达点E,即BE=20米,测得∠AEB=β,已知sin α=  ,tan β=3,求A、B两点间的距离.
解析　如图,过点A作AF⊥CD于点F,∴∠AFB=90°,在Rt△ ABF中,sin α= = ,∴设AF=24x米,AB=25x米,由勾股定理得BF= = =7x米,在Rt△AFE中,tan β= =3,∵BE=20米,∴ =3,解得x=20,∴AB=25x=500米,即A、B两点间的距离为500米. 
4.(2024吉林长春宽城二模)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”形道路连通,其中AB段与高速公路l1成30°角,长为20 km,BC段与AB、CD段都垂直,BC段长10 km,CD段长30 km,求两高速公路间的距离(结果保留根号). 
解析　如图,过B点作l1的垂线,分别交l1,CD,l2于点E,F,G.在Rt △ABE中,∠EAB=30°,∴BE=AB·sin 30°=20× =10(km),∵BC段与AB、CD段都垂直,∴AB∥CD,∠C=∠ABC=90°,∵∠EAB=30°,∴∠ABE=60°,∴∠CBF=30°,∴∠FDG=30°.在Rt△BCF中,BF= =10÷ = (km),CF=BC·tan 30°=10× = (km),∴DF=CD-CF= km,在Rt△DFG中,FG=DF·sin 30°=  × = km,∴EG=BE+BF
+FG=(25+5 )km,故两高速公路间的距离为(25+5 )km. 
5.(2023海南中考)如图,一艘轮船在A处测得灯塔M位于A的 北偏东30°方向,轮船沿着正北方向航行20海里到达B处,测得 灯塔M位于B的北偏东60°方向,测得港口C位于B的北偏东45 °方向.已知港口C在灯塔M的正北方向上.(1)填空:∠AMB=　　　    度,∠BCM=　　　    度;(2)求灯塔M到轮船航线AB的距离(结果保留根号);(3)求港口C与灯塔M的距离(结果保留根号).
解析　如图,分别过点C作CD⊥AB,过点M作ME⊥AB,垂足分 别为D、E.(1)∵∠DBM=∠A+∠AMB=60°,∠A=30°,∴∠AMB=30°.易知 AB∥CM.∵∠DBC=45°,∴∠BCM=45°.(2)由(1)知∠A=∠AMB,∴AB=BM=20海里.在Rt△EBM中,sin∠EBM= ,∴EM=BM·sin∠EBM=20×sin 60°=20× =10 (海里),故灯塔M到轮船航线AB的距离为10 海里.(3)∵CD⊥AB,ME⊥AB,AB∥CM,∴四边形DEMC是矩形.
∴CD=EM=10 海里,DE=CM.在Rt△CDB中,∵∠DBC=45°,∴∠DBC=∠DCB.∴DB=DC=10 海里.在Rt△EMB中,cs∠EBM= ,∴EB=BM·cs∠EBM=20×cs 60°=20× =10(海里),∴CM=DE=DB-EB=10 -10=10( -1)海里,故港口C与灯塔M的距离为10( -1)海里. 
6.(2024吉林长春第二实验中学月考)如果方程x2-4x+3=0的两 个根分别是Rt△ABC两条边的边长,△ABC最小的角为∠A, 求tan A的值.
解析　∵x2-4x+3=0,∴(x-1)(x-3)=0,解得x1=1,x2=3,∵方程x2-4x +3=0的两个根分别是Rt△ABC两条边的边长,△ABC最小的 角为∠A,∴分情况求解如下:(1)如图1,当BC=1,AC=3时,tan A= = ; 图1     图2
(2)如图2,当BC=1,BA=3时,AC=2 ,∴tan A= = = .
综上所述,tan A的值为 或 .
7.(2024河南洛阳第二外国语学校月考)如图,AB=6,O是AB的 中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为 直角三角形时,求AP的长. 
解析　分四种情况讨论求解:(1)当∠APB=90°时,如图1,∵AO=BO,∴PO=AO,∵∠1=120°, ∴∠AOP=60°,∴△AOP为等边三角形,∴∠OAP=60°,∴∠ PBA=30°,∴AP= AB=3.(2)当∠APB=90°时,如图2,∵AO=BO,∠APB=90°,∴PO=BO, ∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP =60°,∴AP=AB·sin 60°=6× =3 .(3)当∠BAP=90°时,如图3,∵∠1=120°,∴∠AOP=60°,∴AP=
OA·tan∠AOP=3× =3 .(4)当∠ABP=90°时,如图4,∵∠1=120°,∴∠BOP=60°,∵OB=3,∴PB=3 ,∴PA= = = =3 . 图1　     图2  图3　      图4综上所述,AP的长为3或3 或3 .
8.(2023内蒙古呼伦贝尔中考)某数学兴趣小组借助无人机测 量一条河流的宽度CD.如图所示,一架水平飞行的无人机在A 处测得河流左岸C处的俯角为α,无人机沿水平线AF方向继 续飞行12米至B处,测得河流右岸D处的俯角为30°,无人机距 地面的铅直高度AM=24 米,点M,C,D在同一条直线上,其中tan α=2.求河流的宽度CD.(结果精确到1米,参考数据: ≈1.7)
解析　如图,过点B作BE⊥MD于点E,则四边形AMEB是矩形, ∴BE=AM=24 米,ME=AB=12米,∵AF∥MD,∴∠ACM=α.在Rt△AMC中,∠AMC=90°,∴tan α= =2,∴ =2,∴MC=12 米,在Rt△BDE中,∠BED=90°,∠DBE=90°-30°=60°,∴tan∠DBE= ,∴tan 60°= = ,∴DE=72米,∴CD=DE-CE=DE-(MC-ME)=72-(12 -12)=84-12 ≈84-12×1.7≈64(米),即河流的宽度CD约为64米.
9.(2024河南南阳卧龙期末)如图,在一条笔直的东西向海岸 线l上有一长为1.5 km的码头MN和一灯塔C,灯塔C距码头的 东端N有20 km.一轮船以36 km/h的速度航行,上午10:00在A 处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测 得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12 km.
(1)若轮船照此速度与航向继续航行,何时到达海岸线?(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由. (参考数据: ≈1.4, ≈1.7)
解析    (1)如图,延长AB交海岸线l于点D,过点B作BE⊥l于 点E,过点A作AF⊥l于F,∴∠BEC=∠AFC=90°,∵∠EBC=60°, ∠CAF=30°,∴∠ECB=30°,∠ACF=60°,∴∠BCA=90°,∵BC=12 km,AB=36× =24(km),∴AB=2BC,∴∠BAC=30°,∴∠ABC=60°,∵∠ABC=∠BDC+∠BCD=60°,∴∠BDC=∠BCD= 30°,∴BD=BC=12 km,∴时间t= = 小时=20分钟,