华东师大版初中数学九年级上册第25章随机事件的概率素养综合检测课件

这是一份华东师大版初中数学九年级上册第25章随机事件的概率素养综合检测课件，共47页。

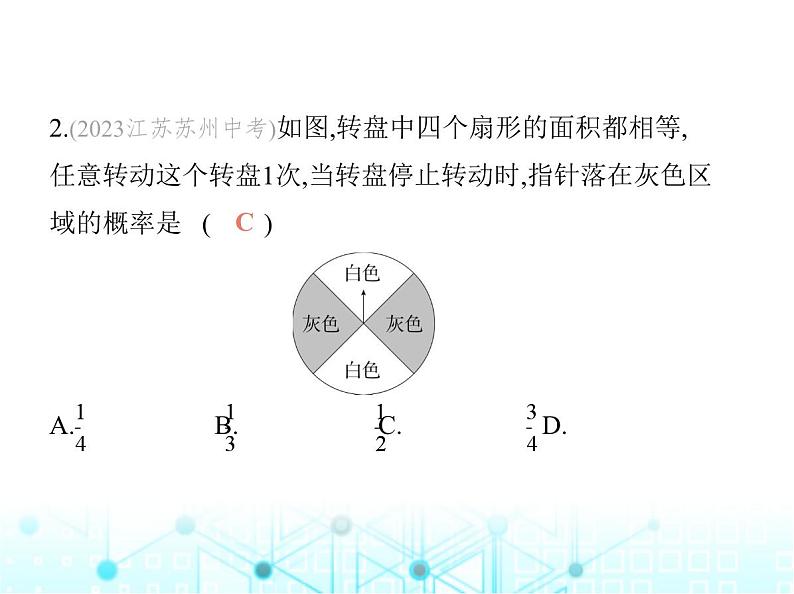
九年级 上册 华东师大版初中数学第25章　素养综合检测(满分100分, 限时60分钟)一、选择题(每小题4分,共32分)1.(2023湖北襄阳中考)襄阳气象台发布的天气预报显示,明天襄阳某地下雨的可能性是75%,则“明天襄阳某地下雨”这一事件是 (　    )A.必然事件　　　    B.不可能事件C.随机事件　　　    D.确定性事件C解析　明天襄阳某地下雨的可能性是75%,是说“明天襄阳某地下雨”的可能性较大,但也不一定会下雨,因此是随机事件.2.(2023江苏苏州中考)如图,转盘中四个扇形的面积都相等,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是 (　    ) A. 　　　    B. 　　　    C. 　　　    D. C解析　∵圆被等分成4份,其中灰色区域占2份,∴指针落在灰色区域的概率为 = .3.(2022贵州贵阳中考)某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定,以抽签方式决定每个人的出场顺序,主持人将表示出场顺序的数字1,2,3分别写在3张同样的纸条上,并将这些纸条放在一个不透明的盒子中,搅匀后从中任意抽出一张,小星第一个抽,下列说法中正确的是 (　    )A.小星抽到数字1的可能性最小B.小星抽到数字2的可能性最大C.小星抽到数字3的可能性最大DD.小星抽到每个数的可能性相同解析　∵3张同样的纸条上分别写有1,2,3,∴小星抽到数字1,2,3的可能性均是 ,∴小星抽到每个数的可能性相同.4.(跨学科·英语)(2023内蒙古通辽中考)在英语单词polynomial(多项式)中任意选出一个字母,选出的字母为“n”的概率是 (　    )A. 　　　    B. 　　　    C. 　　　    D. A5.(2023北京中考)先后两次抛掷同一枚质地均匀的硬币,则第一次正面向上、第二次反面向上的概率是 (　    )A. 　　　    B. 　　　    C. 　　　    D. A6.(2023河南中考)为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神,某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看,则这两个年级选择的影片相同的概率为 (　    )B A. 　　　    B. 　　　    C. 　　　    D. 解析　把三部影片分别记为A、B、C,依题意画树状图如下,由图可知共有9种等可能的结果,其中七、八年级选择的影片相同的结果有3种,∴这两个年级选择的影片相同的概率为 = .  7.(2023江苏连云港中考)下图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点P,则点P落在阴影部分的概率为 (　    ) A. 　　　    B. 　　　    C. 　　　    D. B解析　设16个相同的小正方形的边长为a,则4个相同的大正方形的边长为1.5a,∴点P落在阴影部分的概率为 = .8.(2023山东烟台中考)如图,在正方形中,阴影部分是以正方形的顶点及其对称中心为圆心,以正方形边长的一半为半径作弧形成的封闭图形.将一个小球在该正方形内自由滚动,小球随机地停在正方形内的某一点上.若小球停在阴影部分的概率为P1,停在空白部分的概率为P2,则P1与P2的大小关系为 (　    ) BA.P1P2　　　    D.无法判断解析　如图,连结HF,EG,则阴影部分被分为4部分,其面积分别记为S1,S2,S3,S4.由正方形和圆的性质易知,S1+S2=S3+S4=S正方形AEOH= S正方形ABCD,∴S阴影=S1+S2+S3+S4= S正方形ABCD,S空白= S正方形ABCD,∴P1=P2= ,故选B.二、填空题(每小题4分,共20分)9.(2023甘肃兰州中考)某学习小组做抛掷一枚瓶盖的试验,整理的试验数据如表:下面有三个推断:①通过上述试验的结果,可以推断这枚瓶盖有很大的可能性不是质地均匀的;②第2 000次试验的结果一定是“盖面朝上”;③随着试验次数的增大,“盖面朝上”的概率接近0.53.其中正确的是　　　    .(填序号)①③解析　通过试验的结果,可以推断随着试验次数的增大,“盖面朝上”的概率接近0.53,故可知这枚瓶盖有很大的可能性不是质地均匀的,同时第2 000次试验的结果也不一定是“盖面朝上”.10.(新考向·开放型试题)(2023山西太原小店现代双语学校南校月考)写一个你喜欢的实数m的值:　　     ,使得事件“对于一次函数y=(m-1)x+1,y随x的增大而增大”成为必然事件.答案不唯一,如2解析　当m-1>0,即m>1时,y随x的增大而增大,所以实数m的值可以是2,使得事件“对于一次函数y=(m-1)x+1,y随x的增大而增大”成为必然事件.11.(2023河南南阳邓州期末)新高考“3+1+2”选科模式是指除“语文、数学、外语”3门科目以外,学生应在2门首选科目“历史和物理”中选择1科,然后在4门再选科目“思想政治、地理、化学、生物”中选择2科.小刚同学从4门再选科目中随机选择2科,则恰好选中“思想政治和生物”的概率为　　　    .   解析　依题意列表如下,由表可知共有12种等可能的结果,其中恰好选中“思想政治和生物”的结果有2种,故恰好选中“思想政治和生物”的概率为 = .12.(教材变式·P133T2)(2023四川达州通川六校联考期末)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个面积为20 cm2的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了图②所示的折线统计图,由此估计不规则图案的面积为　　    cm2.7  图① 图②解析　假设不规则图案的面积为x cm2,∵长方形面积为20 cm2,∴小球落在不规则图案上的概率为 ,由折线图可知,随着试验次数的增加,小球落在不规则图案上的频率稳定在0.35左右,则小球落在不规则图案上的概率大约为0.35,∴ =0.35,解得x=7,∴估计不规则图案的面积为7 cm2.13.(2024河南驻马店泌阳二模)甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两个人先打,规则如下:三个人同时各用一只手随机出示手心或手背,若只有两个人手势相同(都是手心或都是手背),则这两人先打,若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是　　　    . 解析　分别用A,B表示手心,手背,依题意画树状图如下,由图可知共有8种等可能的结果,通过一次“手心手背”游戏能决定甲打乒乓球的结果有4种,故通过一次“手心手背”游戏能决定甲打乒乓球的概率是 = .  三、解答题(共48分)14.(新独家原创)(6分)“覆巢无完卵,国破家亦残.岳母忍刺字,千秋大义传.”这是一段穿越千年的历史佳话和一笔宝贵的母教文化遗产.河南汤阴县是岳飞故里,该地某学校组织学生开展公益宣传活动,成立了“岳”“母”“刺”“字”四个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,求他们恰好选到同一个宣传队的概率.解析　把“岳”“母”“刺”“字”四个宣传队分别记为A,B,C,D,画树状图如下,由图可知共有16种等可能的结果,小华和小丽恰好选到同一个宣传队的结果有4种,故P(小华和小丽恰好选到同一个宣传队)= = .15.(6分)(跨学科·语文)汉字是世界上最古老的文字之一.字形结构体现着人类追求均衡对称、和谐稳定的天性.如图所示,三个汉字可以看成轴对称图形,小敏和小慧利用“土”“口”“木”三个汉字设计了一个游戏,规则:将这三个字分别写在背面都相同的三张卡片上,背面朝上,洗匀后抽出一张,放回洗匀后再抽出一张,若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”),则小敏获胜;否则小慧获胜,你认为这个游戏对谁有利?说明理由.  解析　这个游戏对小慧有利.理由:画树状图如下: 共有9种等可能的结果,其中能构成上下结构的汉字的结果有4种:(土,土)构成“圭”,(口,口)构成“吕”,(口,木)构成“呆”或“杏”,(木,口)构成“杏”或“呆”,∴P(小敏获胜)= ,P(小慧获胜)= ,∵ < ,∴游戏对小慧有利.16.(2024吉林长春九台二模)(8分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.(1)先从袋子中取出m个红球(m>1且m为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.①若事件A为必然事件,则m的值为　　　    ;②若事件A为随机事件,则m的值为　　　    .(2)先从袋子中取出m个红球,再放入m个一样的黄球并摇匀,经过多次试验,随机摸出一个黄球的频率在 附近摆动,求m的值.解析    (1)①当袋子中全为黄球,即取出4个红球时,摸到黄球是必然事件,则m=4.②当取出2个或3个红球,即m=2或3时,摸到黄球为随机事件.(2)由题意得 = ,解得m=2.17.(情境题·革命文化)(2023甘肃武威中考)(8分)为传承红色文化,激发革命精神,增强爱国主义情感,某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学之旅,策划了三条红色线路让学生选择:A.南梁精神红色记忆之旅(华池县);B.长征会师胜利之旅(会宁县);C.西路军红色征程之旅(高台县),且每人只能选择一条线路.小亮和小刚两人用抽卡片的方式确定一条自己要去的线路.他们准备了3张不透明的卡片,正面分别写上字母A,B,C,卡片除正面字母不同外其余均相同,将3张卡片正面向下洗匀,小亮先从中随机抽取一张卡片,记下字母后正面向下放回,洗匀后小刚再从中随机抽取一张卡片.(1)求小亮从中随机抽到卡片A的概率;(2)请用画树状图或列表的方法,求两人都抽到卡片C的概率.解析    (1)小亮从中随机抽到卡片A的概率为 .(2)画树状图如下,由图可知共有9种等可能的结果,其中小亮和小刚两人都抽到卡片C的结果有1种,故两人都抽到卡片C的概率是 .  18.(新课标例88变式)(2023云南中考)(10分)甲、乙两名同学准备参加种植蔬菜的劳动实践活动,各自随机选择种植辣椒、种植茄子、种植西红柿三种中的一种,记种植辣椒为A,种植茄子为B,种植西红柿为C.假设这两名同学选择种植哪种蔬菜不受任何因素影响,且每一种被选到的可能性相等.记甲同学的选择为x,乙同学的选择为y.(1)请用列表法或画树状图法中的一种,求(x,y)所有可能出现的结果总数;(2)求甲、乙两名同学选择种植同一种蔬菜的概率P.解析    (1)依题意画树状图如下,由图可知共有9种等可能的结果,分别为(A,A)、(A,B)、(A,C)、(B,A)、(B,B)、(B,C)、(C,A)、(C,B)、(C,C). (2)由(1)可知,共有9种等可能的结果,其中甲、乙两名同学选择种植同一种蔬菜的结果有3种,故甲、乙两名同学选择种植同一种蔬菜的概率P= = .19.(2023四川眉山中考)(10分)某校为落实“双减”工作,推行“五育并举”,计划成立五个兴趣活动小组(每个学生只能参加一个活动小组):A.音乐,B.美术,C.体育,D.阅读,E.人工智能.为了解学生对以上兴趣活动的参与情况,随机抽取了部分学生进行调查统计,并根据统计结果,绘制成了如图所示的两幅不完整的统计图:  根据图中信息,完成下列问题:(1)①补全条形统计图(要求在条形统计图上方注明人数);②扇形统计图中的圆心角α的度数为　　　    .(2)若该校有3 600名学生,估计该校参加E组(人工智能)的学生人数.(3)该学校从E组中挑选出了表现最好的两名男生和两名女生,计划从这四名学生中随机抽取两人参加市青少年人工智能竞赛,请用画树状图或列表的方法求出恰好抽到一名男生和一名女生的概率.解析    (1)①由题意知,被调查的总人数为30÷10%=300,所以D小组人数为300-(40+30+70+60)=100,补全统计图如下: ②扇形统计图中的圆心角α的度数为360°× =120°.(2)3 600× =720(名),故估计该校参加E组(人工智能)的学生有720名.(3)依题意画树状图如下,由图可知共有12种等可能的结果,其中一名男生和一名女生的结果数为8,故恰好抽到一名男生和一名女生的概率为 = .