




初中第23章 图形的相似23.3 相似三角形2. 相似三角形的判定课前预习课件ppt
展开第3课时 相似三角形的判定定理
知识点5 相似三角形的判定定理2
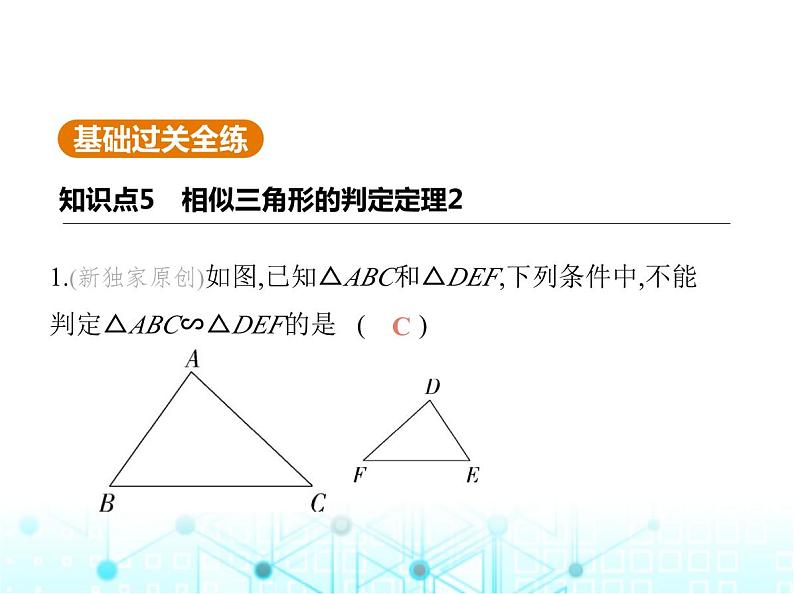
1.(新独家原创)如图,已知△ABC和△DEF,下列条件中,不能 判定△ABC∽△DEF的是 ( )
A.∠A=∠D, = B.∠B=∠E, = C.∠B=∠F, = D.∠C=∠F, =
解析 C选项不满足两边成比例且夹角相等的条件,故不能 判定△ABC∽△DEF.
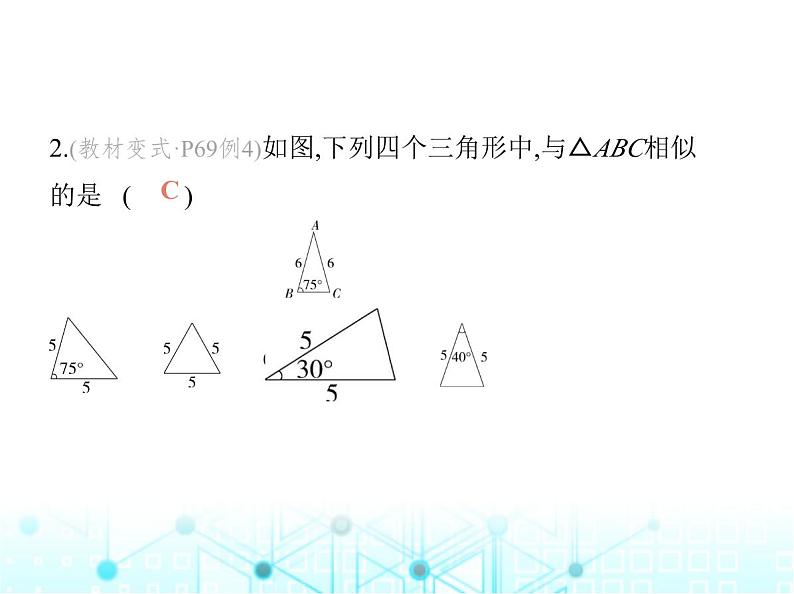
2.(教材变式·P69例4)如图,下列四个三角形中,与△ABC相似 的是 ( ) A B C D
解析 由题图可知,AB=AC=6,∴∠C=∠B=75°,∴∠A=30°.根 据两边成比例且夹角相等的两个三角形相似,易知与△ABC 相似的是选项C中的三角形.
3.(情境题·现实生活)(2023江苏镇江中考)如图,用一个卡钳 测量某个零件的内孔直径AB,量得CD的长度为6 cm,则AB等于 cm.
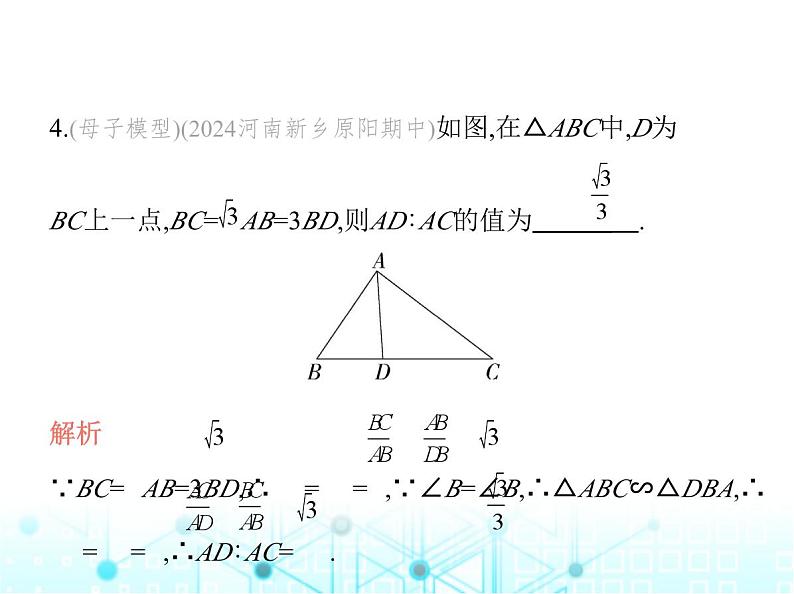
4.(母子模型)(2024河南新乡原阳期中)如图,在△ABC中,D为 BC上一点,BC= AB=3BD,则AD∶AC的值为 .
5.(2024福建泉州鲤城培元中学月考)如图,在△ABC中,BD⊥ AC于点D,DE⊥AB于点E,BD·DE=BE·CD.(1)求证:△BCD∽△BDE;(2)若BC=10,AD=6,求AE的长.
解析 (1)证明:∵BD⊥AC于点D,DE⊥AB于点E,∴∠BDC= ∠BED=90°,∵BD·DE=BE·CD,∴ = ,∴△BCD∽△BDE.(2)∵△BCD∽△BDE,∴∠EBD=∠DBC,∵BD⊥AC,∴CD= AD=6,BA=BC=10,∴BD= =8,∵△BCD∽△BDE,∴ = ,∴ = ,∴BE= ,∴AE=BA-BE=10- = .
6.(新考法)(2024河南开封杞县二模,9,★★☆)如图,已知直线 y=- x+2与x轴交于点A,与y轴交于点B,在x轴上有一点C,使B、O、C三点构成的三角形与△AOB相似,则点C的坐标 为( )
A.(-1,0)或(1,0)B.(4,0)或(-4,0)C.(-1,0)或 (-4,0) D.(-1,0)或(1,0)或(-4,0)或(4,0)
解析 本题将相似三角形的判定与一次函数综合在一起考 查,比较新颖.∵直线y=- x+2与x轴交于点A,与y轴交于点B,∴A(4,0),B(0,2),∴OA=4,OB=2.分情况求解如下:(1)当△AOB∽△BOC时, = ,即 = ,解得OC=1,∴C(-1,0)或(1,0);(2)当△AOB∽△COB时, = =1,∴C(4,0)或(-4,0).综上所述,点C的坐标为(-1,0)或(1,0)或(4,0)或(-4,0).
7.(易错题)(2024湖南衡阳衡东二模,15,★★☆)将三角形纸片 (△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF.已知AB=AC=3,BC=4,若以点B'、F、C为顶点的 三角形与△ABC相似,那么BF的长度是 .
解析 由折叠易知,BF=B'F,根据△B'FC与△ABC相似时的对 应关系,有两种情况:(1)△B'FC∽△ABC时, = ,∵AB=AC=3,B'F=BF,∴ = ,解得BF= ;(2)△B'CF∽△BCA时, = ,∵AB=AC=3,∴B'F=CF,∵BF=B'F,∴BF=CF= BC=2.综上所述,BF的长度是 或2.
易错点:相似三角形的对应关系不确定时,需分类讨论,避免 产生漏解的错误.
8.(2024吉林长春双阳二模,23,★★☆)如图,在四边形ABCD 中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连结DF,且满足CF=EC.(1)求证:BD⊥DF;(2)当BC2=DE·DB时,试判断四边形DECF的形状,并说明理由.
解析 (1)证明:∵∠BCD=∠ECF=90°,∴∠BCE=∠DCF,∵BC=DC,EC=CF,∴△BCE≌△DCF,∴∠EBC=∠FDC,∵BC= DC,∠BCD=90°,∴∠DBC=∠BDC=45°,∴∠FDC=45°,∴∠FDB=∠FDC+∠BDC=90°,∴BD⊥DF.(2)四边形DECF是正方形.理由:∵BC2=DE·DB,BC=DC,∴DC 2=DE·DB,∴ = ,∵∠CDE=∠BDC,∴△CDE∽△BDC,∴∠DEC=∠DCB=90°,∵∠FDE=∠ECF=90°,∴四边形 DECF是矩形,∵CE=CF,∴四边形DECF是正方形.
9.(推理能力)(2024四川乐山沐川模拟)如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3 cm,OB=4 cm,动点E,F同时从O点出发,点E以1.5 cm/s的速度 沿ON方向运动,点F以2 cm/s的速度沿OM方向运动,EF与OA 交于点C,连结AE,当点E到达点B时停止运动,点F随之停止运 动.设运动时间为t s(t>0).
(1)当t=1时,△EOF与△ABO是否相似?请说明理由.(2)在运动过程中,无论t取何值,总有EF⊥OA,为什么?
浙教版九年级上册4.4 两个三角形相似的判定教课ppt课件: 这是一份浙教版九年级上册<a href="/sx/tb_c98877_t3/?tag_id=26" target="_blank">4.4 两个三角形相似的判定教课ppt课件</a>,共22页。PPT课件主要包含了方法2预备定理,方法3判定定理1,合作探索等内容,欢迎下载使用。
初中数学浙教版九年级上册4.4 两个三角形相似的判定课堂教学课件ppt: 这是一份初中数学浙教版九年级上册<a href="/sx/tb_c98877_t3/?tag_id=26" target="_blank">4.4 两个三角形相似的判定课堂教学课件ppt</a>,共22页。PPT课件主要包含了①与⑥,②与④,③与⑤等内容,欢迎下载使用。
初中数学沪科版九年级上册22.2 相似三角形的判定教学ppt课件: 这是一份初中数学沪科版九年级上册<a href="/sx/tb_c44093_t3/?tag_id=26" target="_blank">22.2 相似三角形的判定教学ppt课件</a>,共15页。PPT课件主要包含了知识要点,新知导入,①和③,你的判断依据是什么,课程讲授,ADAB,成比例,随堂练习,解相似,理由如下等内容,欢迎下载使用。













