






初中华师大版2. 图形的变换与坐标教案配套ppt课件
展开第2课时 图形的变换与坐标
知识点3 平移变换与坐标
1.(2023浙江绍兴中考)在平面直角坐标系中,将点(m,n)先向 右平移2个单位,再向上平移1个单位,最后所得点的坐标是 ( )A.(m-2,n-1) B.(m-2,n+1)C.(m+2,n-1) D.(m+2,n+1)
解析 平面直角坐标系中点的坐标的平移规律:横坐标,右移 加,左移减;纵坐标,上移加,下移减.
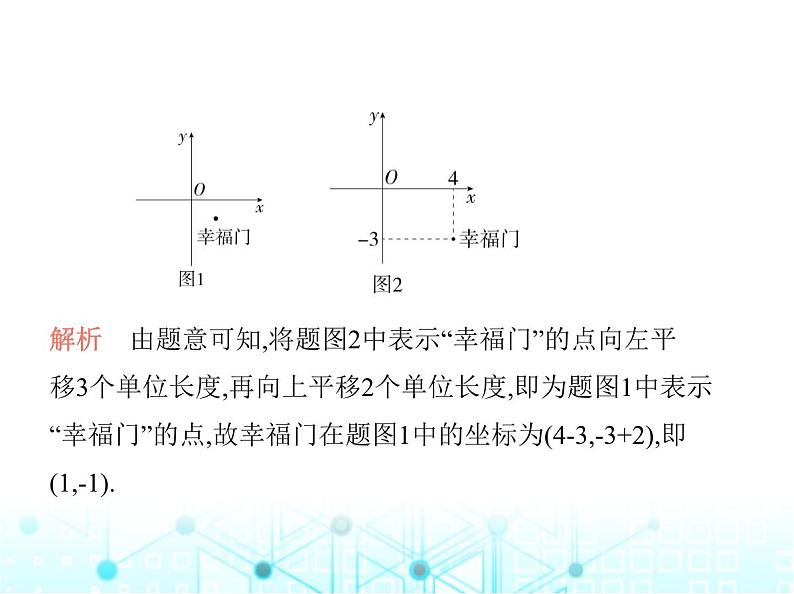
2.(新独家原创)幸福门被誉为“威海之门”,是威海的地标 性建筑,代表着威海现代化的城市形象.小明以威海市的两条 公路为x轴和y轴建立直角坐标系,如图1所示,幸福门处于该 坐标系的第四象限.他将该坐标系的x轴向上平移2个单位长 度,y轴向左平移3个单位长度,如图2所示,幸福门在该坐标系 中的坐标为(4,-3),求幸福门在图1中的坐标.
解析 由题意可知,将题图2中表示“幸福门”的点向左平 移3个单位长度,再向上平移2个单位长度,即为题图1中表示 “幸福门”的点,故幸福门在题图1中的坐标为(4-3,-3+2),即 (1,-1).
知识点4 轴对称变换与坐标
3.(2022浙江台州中考)如图所示的是战机在空中展示的轴对 称队形.以飞机B,C所在直线为x轴、队形的对称轴为y轴,建 立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标 为 ( )A.(40,-a)B.(-40,a)
C.(-40,-a) D.(a,-40)
解析 ∵飞机E(40,a)与飞机D关于y轴对称,∴飞机D的坐标 为(-40,a).
4.(2024河南南阳镇平期中)如图,一只跳蚤从M点出发,先向 上爬行了2个单位,又向左爬行了3个单位到达P点,然后跳到 与点P关于x轴对称的点P1处,则点P1的坐标为 .
解析 由题意知点P的坐标为(0-3,1+2),即(-3,3),∵点P与点P1关于x轴对称,∴P1的坐标为(-3,-3).
知识点5 旋转变换与坐标
5.(2024辽宁大连名校联盟期末)如图,将线段AB绕点O顺时针 旋转90°得到线段A'B',那么A(-1,4)的对应点A'的坐标是 .
解析 ∵线段AB绕点O顺时针旋转90°得到线段A'B',∴△ABO≌△A'B'O,∠AOA'=90°,∴AO=A'O.如图,作AC⊥y轴于C,
A'C'⊥x轴于C',∴∠ACO=∠A'C'O=90°.∵∠COC'=90°,∴∠AOA'-∠COA'=∠COC'-∠COA',∴∠AOC=∠A'OC'.在△ACO 和△A'C'O中,∵ ∴△ACO≌△A'C'O,∴AC=A'C',CO=C'O.∵A(-1,4),∴AC=1,CO=4,∴A'C'=1,OC'=4,∴A'(4,1).
6.(2023山东枣庄中考)银杏是著名的活化石植物,其叶有细 长的叶柄,呈扇形.如图所示的是一片银杏叶标本,叶片上B,C 两点的坐标分别为(-3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A的对应点的坐标为 .
解析 根据题意建立平面直角坐标系,如图,那么点A的坐标 为(-1,-3),作出点A绕原点O顺时针旋转90°所得的对应点A', 则点A'的坐标为(-3,1).
知识点6 位似变换与坐标
7.(易错题)(2023辽宁盘锦中考)如图,△ABO的顶点是A(2,6), B(3,1),O(0,0),以点O为位似中心,将△ABO各边缩小为原来的 ,得到△A'B'O,则点A'的坐标为 .
解析 本题易因考虑问题不全面致错.∵以原点O为位似中 心,把△ABC各边缩小为原来的 ,得到△A'B'O,点A的坐标为(2,6),∴点A'的坐标是 或 ,即 ,2 或 .
8.(新独家原创)如图,在平面直角坐标系中,△ABC三个顶点 分别为A(-2,-2),B(-5,-4),C(-1,-5).(1)以点O为位似中心,把△ABC各边放大为原来的2倍,在y轴 右侧得△A1B1C1,请在网格中画出△A1B1C1;(2)求经过点A1的反比例函数y= 的解析式,并求当4
经过点A1,∴k=4×4=16,∴反比例函数y= 的解析式为y= .当y=4时,x= =4;当y=8时,x= =2,∴当4
A.(1,-3) B.(3,-1)C.(-3,-1) D.(-3,1)
解析 ∵P(-3,1),∴点P关于直线y=-x的对称点P1(-1,3),P1关 于y轴的对称点P2(1,3),P2关于x轴的对称点P3(1,-3),P3关于直 线y=-x的对称点P4(3,-1),P4关于y轴的对称点P5(-3,-1),P5关于x 轴的对称点P6(-3,1),∴6次变换为一循环.∵2 021÷6=336…… 5,∴点P2 021的坐标与点P5的坐标相同,∴P2 021(-3,-1).
10.(2021湖北仙桃中考,16,★★☆)如图,在平面直角坐标系 中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向 下平移1个单位长度得到点P1(-1,-1);接着水平向右平移2个 单位长度,再竖直向上平移2个单位长度得到点P2;接着水平 向左平移3个单位长度,再竖直向下平移3个单位长度得到点 P3;接着水平向右平移4个单位长度,再竖直向上平移4个单位 长度得到点P4,……,按此作法进行下去,则点P2 021的坐标为 .
(-1 011,-1 011)
解析 观察图形可知奇数点在第三象限,∵P1(-1,-1),P3(-2,-2),P5(-3,-3),…,P2n-1(-n,-n),∴P2 021(-1 011,-1 0 11).
11.(2024四川成都郫都二模,18,★★☆)如图,已知点A(1,0)、 B(0,2)及双曲线y=6x-1(x>0).若以点P为位似中心,将△AOB各 边放大为原来的两倍后得到对应的△DEF,使得点D、F恰好 在双曲线上,则点P的坐标为 .
(-1,-2)或(1,2)
解析 分情况求解如下:①当点P在第三象限时,如图,∵将△AOB各边放大为原来的 两倍后得到△DEF,∴EF=4,DE=2,∵点D,F恰好在反比例函 数y= 的图象上,∴设F ,∴D ,∴(m+2) =6,解得m=1或-3(舍),经检验,m=1是原方程的解,∴F(1,6),D(3,2),∴E(1,2),从而易知直线BF的解析式为y=4x+2,直 线AD的解析式为y=x-1,令4x+2=x-1,解得x=-1,∴y=-2,∴P(-1,-2);
②当点P在第一象限时,如图,可知点P与①中的E重合,∴P(1, 2).综上所述,点P的坐标为(-1,-2)或(1,2).
12.(2024山西长治二模,23,★☆☆)如图,在平面直角坐标系 内,△ABC三个顶点分别为A(1,-2),B(4,-1),C(3,-3).(1)作出△ABC向左平移5个单位长度,再向下平移3个单位长 度得到的△A1B1C1;(2)以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A2B2C2,作出△A2B2C2;(3)以坐标原点O为旋转中心,将△ABC逆时针旋转90°,得到 △A3B3C3,作出△A3B3C3.
解析 (1)如图,△A1B1C1即为所作.(2)如图,△A2B2C2即为所作.(3)如图,△A3B3C3即为所作.
13.(几何直观)(2021辽宁阜新中考)下面是小明关于“对称与 旋转的关系”的探究过程,请你补充完整.(1)三角形在平面直角坐标系中的位置如图1所示,简称G,G关 于y轴的对称图形为G1,关于x轴的对称图形为G2,则将图形G1 绕 点顺时针旋转 度,可以得到图形G2.(2)在图2中分别画出G关于y轴和直线y=x+1的对称图形G1,G 2.将图形G1绕点 (用坐标表示)顺时针旋转 度,可以得到图形G2.
(3)综上,如图3,直线l1:y=-2x+2和l2:y=x所夹锐角为α°,如果G关于直线l1的对称图形为G1,关于直线l2的对称图形为G2,那么将 图形G1绕点 (用坐标表示)顺时针旋转 度 (用α表示),可以得到图形G2. 图1 图2
解析 (1)O;180.(2)G关于y轴和直线y=x+1的对称图形G1,G2如图所示,将G1绕 点(0,1)顺时针旋转90度,可以得到图形G2. (3) ;2α.
由(1)知当G关于y轴的对称图形为G1,关于x轴的对称图形为 G2时,G1与G2关于原点(0,0)对称,即图形G1绕点O顺时针旋转180度,可以得到图形G2,点(0,0)为x轴与y轴的交点,180°角为x 轴与y轴夹角的两倍;由(2)知当G关于y轴的对称图形为G1,关于直线y=x+1的对称 图形为G2时,图形G1绕点(0,1)顺时针旋转90度,可以得到图形 G2,点(0,1)为直线y=x+1与y轴的交点,90度角为直线y=x+1与y 轴所夹锐角的两倍.
数学2. 图形的变换与坐标教学ppt课件: 这是一份数学2. 图形的变换与坐标教学ppt课件,共26页。PPT课件主要包含了知识要点,轴对称与坐标,中心对称与坐标,位似与坐标,新知导入,课程讲授,A2-3,B-12,C-3-4,E40等内容,欢迎下载使用。
初中数学华师大版九年级上册2. 图形的变换与坐标作业ppt课件: 这是一份初中数学华师大版九年级上册2. 图形的变换与坐标作业ppt课件,共25页。
初中数学华师大版九年级上册2. 图形的变换与坐标课文配套课件ppt: 这是一份初中数学华师大版九年级上册2. 图形的变换与坐标课文配套课件ppt,共14页。PPT课件主要包含了重点难点,练习一,课堂小结,本节课我的收获是等内容,欢迎下载使用。













