华师大版九年级上册24.4 解直角三角形评课课件ppt

这是一份华师大版九年级上册24.4 解直角三角形评课课件ppt，共26页。
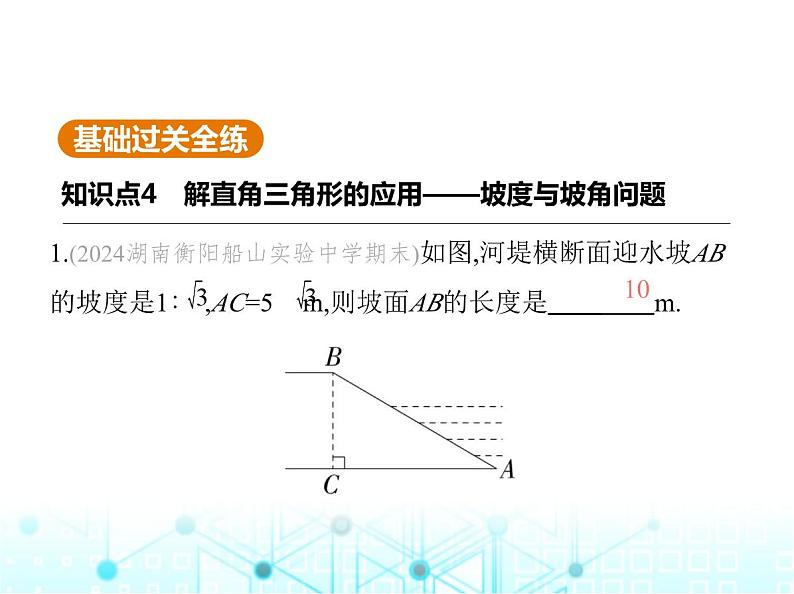
知识点4　解直角三角形的应用——坡度与坡角问题
1.(2024湖南衡阳船山实验中学期末)如图,河堤横断面迎水坡AB的坡度是1∶ ,AC=5  m,则坡面AB的长度是　　        m. 
解析　∵迎水坡AB的坡度是1∶ ,∴ = ,∵AC=5  m,∴BC=5 m,∴AB= =10 m.
2.(2023黑龙江大庆中考)某风景区观景缆车路线如图所示,缆车从点A出发,途经点B后到达山顶P,其中AB=400米,BP=200米,且AB段的运行路线与水平方向的夹角为15°,BP段的运行路线与水平方向的夹角为30°,求垂直高度PC.(结果精确到1米,参考数据:sin 15°≈0.259,cs 15°≈0.966,tan 15°≈0.268) 
解析　如图,过点B作BD⊥PC,垂足为D,过点B作BE⊥AC,垂 足为E,由题意得CD=BE,在Rt△ABE中,∠A=15°,AB=400米, ∴BE=AB·sin 15°≈400×0.259=103.6(米),∴CD=BE=103.6米, 在Rt△BDP中,∠PBD=30°,BP=200米,∴DP= BP=100(米),∴PC=PD+DC≈204(米),∴垂直高度PC约为204米.
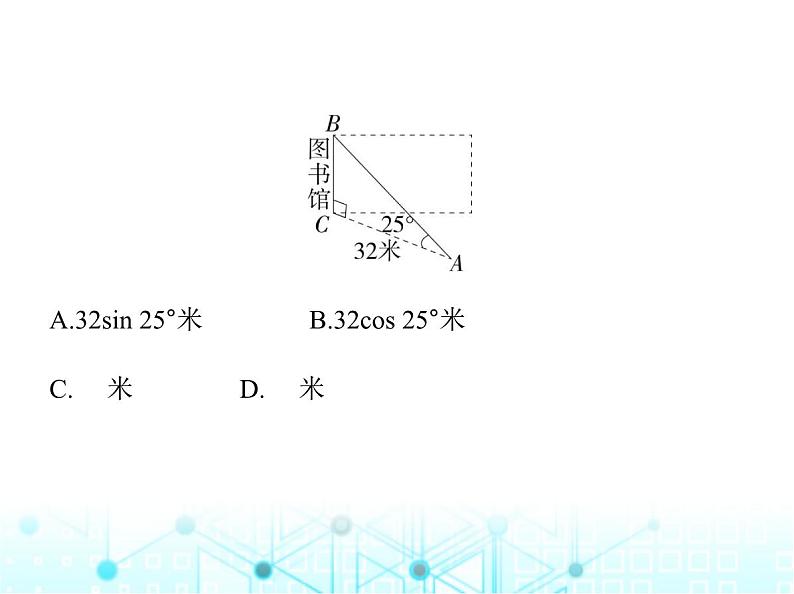
3.(2023吉林长春中考)学校开放日即将来临,负责布置的林 老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面,如 图所示.已知彩旗绳与地面形成25°角(即∠BAC=25°),彩旗绳 固定在地面的位置与图书馆相距32米(即AC=32米),则彩旗 绳AB的长度为(　    )
 A.32sin 25°米　　　    B.32cs 25°米
C. 米　　　    D. 米
解析　由题意知AC=32米,∠A=25°,在Rt△ABC中,∵cs A=  ,∴AB= = 米.
4.(跨学科·语文)(2024福建福州鼓楼屏东中学二模)周末,刘老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起去江边垂钓.如图,钓鱼竿AC的长为4 m,露在水面上的渔线BC的长为2  m,刘老师想看看鱼钩上的情况,把鱼竿AC移到AC'的位置,此时,∠CAC'=15°,则此时露出水面的渔线B'C'的长度是 (　    )
 A.3 m　　　    B.2  m　　　    C.2  m　　　    D.3  m
解析　在Rt△ABC中,AC=4 m,BC=2  m,∴sin∠CAB= = = ,∴∠CAB=45°,∵∠CAC'=15°,∴∠C'AB=∠C'AC+∠CAB=60°,在Rt△C'AB'中,AC'=4 m,∴C'B'=AC'·sin 60°=4×  =2 (m),∴露出水面的渔线B'C'的长度是2  m.
5.(2023江苏盐城中考)如图1,位于市区的“铁军”雕塑“大 铜马”是盐城市标志性文化名片,如图2,线段AB表示“铁 军”雕塑的高,点B,C,D在同一条直线上,且∠ACB=60°,∠ ADB=30°,CD=17.5 m,则线段AB的长约为　　　    m.(计算 结果保留整数,参考数据: ≈1.7)
解析　∵∠ACB=60°,∠ADB=30°,∠ACB=∠ADB+∠CAD,∴ ∠CAD=30°,∴∠ADB=∠CAD,∴AC=CD=17.5 m,∵∠ABC= 90°,∠ACB=60°,∴AB=AC·sin∠ACB=17.5× ≈15(m).
6.(2023浙江台州中考)教室里的投影仪投影时,可以把投影 光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示 的△ABC,∠BAC=90°,黑板上投影图像的高度AB=120 cm,CB 与AB的夹角∠B=33.7°,求AC的长.(结果精确到1 cm.参考数 据:sin 33.7°≈0.55,cs 33.7°≈0.83,tan 33.7°≈0.67)      
解析　在Rt△ABC中,AB=120 cm,∠BAC=90°,∠B=33.7°,tan B = ,∴AC=AB·tan 33.7°≈120×0.67=80.4≈80(cm),即AC的长约为 80 cm.
7.(2023湖北十堰中考,7,★★☆)如图所示,有一天桥AB高5 米,BC是通向天桥的斜坡,∠ACB=45°,市政部门启动“陡改 缓”工程,决定将斜坡的底端C延伸到D处,使∠D=30°,则CD 的长度约为(参考数据: ≈1.414, ≈1.732) (　    ) 
米　　　    米　　　    米　　　    米
8.(情境题·数学文化)(2023浙江杭州中考,10,★★☆)第二十四届国际数学家大会会徽的设计基础是1 700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形 (△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连结BE.设∠BAF= α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为 1∶n,tan α=tan2β,则n= (　    )
 　     A.5　　　    B.4　　　    C.3　　　    D.2
解析　设AE=a,DE=b,则BF=a,AF=b,EF=b-a,∴tan α= ,tan β= ,∵tan α=tan2β,∴ = ,∴(b-a)2=ab,∴a2+b2=3ab,∵a2+b2=AD2=S正方形ABCD,(b-a)2=S正方形EFGH,∴S正方形EFGH∶S正方形ABCD= ab∶3ab=1∶3,∵S正方形EFGH∶S正方形ABCD=1∶n,∴n=3.
9.(新考向·开放型试题)(2024江苏盐城盐都康居路初中教育集团二模,20,★☆☆)已知△ABC为钝角三角形,其中∠A>90°,有下列条件:①AB=10;②AC=6 ;③tan B= ;④tan C= .(1)你认为从中至少选择　　　    个条件,可以求出BC边的 长;(2)你选择的条件是　　　    (填序号),写出求BC边的长的解 答过程.
解析    (1)根据解直角三角形的条件可知,至少选择3个条件, 可以求出BC边的长.(2)答案不唯一,如:选择①②④.理由:如图,过点A作AD⊥BC 于点D,设AD=x,∵tan C= ,∴ = ,∴CD=2x,∵AC=6 ,∴根据勾股定理得x2+(2x)2=(6 )2,解得x=6或x=-6(不合题意,舍去),∴AD=6,CD=2x=12,∵AB=10,∴根据勾股定理得BD=  =8,∴BC=CD+BD=12+8=20.
10.(应用意识)(2024吉林长春汽开区二模)“日照间距系数” 反映了房屋日照情况.如图1,当前后房屋都朝向正南时,日照 间距系数=L∶(H-H1),其中L为楼间水平距离,H为南侧楼房高 度,H1为北侧楼房底层窗台至地面高度,如图2,山坡EF朝北, EF长15 m,其坡度为1∶0.75,山坡顶部平地EM上有一高为24.3 m的楼房AB,底部A到E点的距离为5 m.欲在AB楼正北侧
山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面 C处的高度为1.1 m,要使该楼的日照间距系数不低于1.25,底 部C距F处至少多远?
 图1　     图2
解析　如图,过点E作EQ⊥NF,交NF的延长线于点Q,∵山坡 EF坡度为1∶0.75,∴ = = ,设EQ=4x m,则FQ=3x m,∴EF= =5x m,∵EF=15 m,∴5x=15,解得x=3,∴EQ=4x=12 m,FQ=3x=9 m,由题意得L=CF+FQ+EA=CF+9+5=CF+1 4,H=AB+EQ=24.3+12=36.3(m),H1=1.1 m, ∴日照间距系数=L∶(H-H1)= = ,