中考数学第一轮专题复习真题分点透练(全国通用)第十五讲全等三角形(原卷版+解析)

这是一份中考数学第一轮专题复习真题分点透练(全国通用)第十五讲全等三角形(原卷版+解析)，共19页。
1．（2021•重庆）如图，点B，F，C，E共线，∠B＝∠E，BF＝EC，添加一个条件，不能判断△ABC≌△DEF的是（ ）
A．AB＝DEB．∠A＝∠DC．AC＝DFD．AC∥FD
2．（2022•湖北）如图，已知AB∥DE，AB＝DE，请你添加一个条件 ，使△ABC≌△DEF．
3．（2022•乐山）如图，B是线段AC的中点，AD∥BE，BD∥CE．求证：△ABD≌△BCE．
类型二 轴对称型
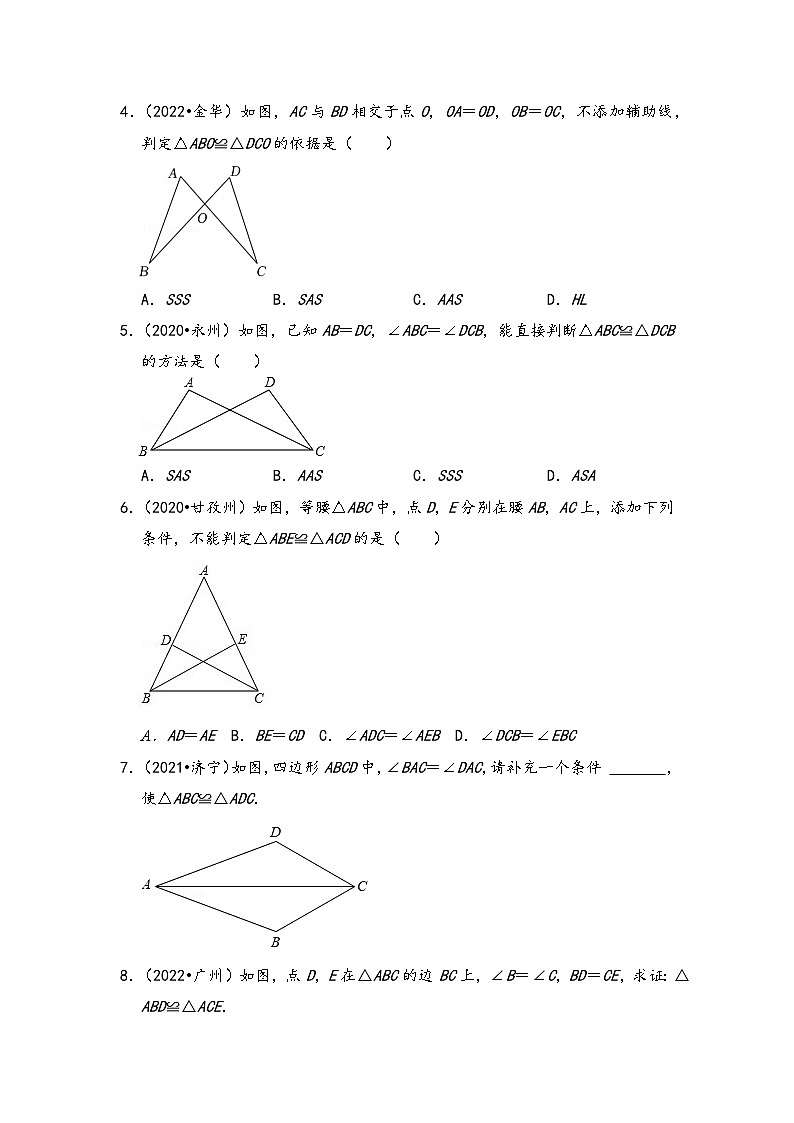
4．（2022•金华）如图，AC与BD相交于点O，OA＝OD，OB＝OC，不添加辅助线，判定△ABO≌△DCO的依据是（ ）
A．SSSB．SASC．AASD．HL
5．（2020•永州）如图，已知AB＝DC，∠ABC＝∠DCB，能直接判断△ABC≌△DCB的方法是（ ）
A．SASB．AASC．SSSD．ASA
6．（2020•甘孜州）如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE≌△ACD的是（ ）
AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC
7．（2021•济宁）如图，四边形ABCD中，∠BAC＝∠DAC，请补充一个条件 ，使△ABC≌△ADC．
8．（2022•广州）如图，点D，E在△ABC的边BC上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE．
9．（2020•柳州）如图，已知OC平分∠MON，点A、B分别在射线OM，ON上，且OA＝OB．
求证：△AOC≌△BOC．
类型三 旋转型
考向1 共顶点旋转
10．（2021•哈尔滨）如图，△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE＝65°，则∠CAF的度数为（ ）
A．30°B．25°C．35°D．65°
11．（2021•齐齐哈尔）如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是 ．（只需写出一个条件即可）
12．（2022•宁夏）如图，AC，BD相交于点O，OB＝OD，要使△AOB≌△COD，添加一个条件是 .（只写一个）
13．（2022•牡丹江）如图，CA＝CD，∠ACD＝∠BCE，请添加一个条件 ，使△ABC≌△DEC．
14．（2021•宜宾）如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．
求证：△AOB≌△COD．
考向2 不共顶点旋转
1．（2021•台湾）已知△ABC与△DEF全等，A、B、C的对应点分别为D、E、F，且E点在AC上，B、F、C、D四点共线，如图所示．若∠A＝40°，∠CED＝35°，则下列叙述何者正确？（ ）
A．EF＝EC，AE＝FCB．EF＝EC，AE≠FC
C．EF≠EC，AE＝FCD．EF≠EC，AE≠FC
类型四 三垂直型
16．（2022•益阳）如图，在Rt△ABC中，∠B＝90°，CD∥AB，DE⊥AC于点E，且CE＝AB．求证：△CED≌△ABC．
17．（2022•铜仁市）如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB＝CD．求证：△ABC≌△CDE．
其他类型
18．（2021•陕西）如图，BD∥AC，BD＝BC，点E在BC上，且BE＝AC．求证：∠D＝∠ABC．
19.（2020•温州）如图，在△ABC和△DCE中，AC＝DE，∠B＝∠DCE＝90°，点A，C，D依次在同一直线上，且AB∥DE．
（1）求证：△ABC≌△DCE．
（2）连接AE，当BC＝5，AC＝12时，求AE的长．
命题点2 全等三角形的实际应用
20．（2021•盐城）工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别截取OC＝OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线．这里构造全等三角形的依据是（ ）
A．SASB．ASAC．AASD．SSS
21．（2021•柳州）如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB，连接DE，那么量出DE的长就是A、B的距离，为什么？请结合解题过程，完成本题的证明．
证明：在△DEC和△ABC中，
，
∴△DEC≌△ABC（SAS），
∴ ．
第十五讲 全等三角形
命题点1 全等三角形的判定与性质
类型一 平移型
1．（2021•重庆）如图，点B，F，C，E共线，∠B＝∠E，BF＝EC，添加一个条件，不能判断△ABC≌△DEF的是（ ）
A．AB＝DEB．∠A＝∠DC．AC＝DFD．AC∥FD
【答案】C
【解答】解：∵BF＝EC，
∴BF+FC＝EC+FC，
∴BC＝EF，
又∵∠B＝∠E，
∴当添加条件AB＝DE时，△ABC≌△DEF（SAS），故选项A不符合题意；
当添加条件∠A＝∠D时，△ABC≌△DEF（AAS），故选项B不符合题意；
当添加条件AC＝DF时，无法判断△ABC≌△DEF，故选项C符合题意；
当添加条件AC∥FD时，则∠ACB＝∠DFE，故△ABC≌△DEF（ASA），故选项D不符合题意；
故选：C．
2．（2022•湖北）如图，已知AB∥DE，AB＝DE，请你添加一个条件 ，使△ABC≌△DEF．
【答案】∠A＝∠D
【解答】解：添加条件：∠A＝∠D．
∵AB∥DE，
∴∠B＝∠DEC，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（ASA），
故答案为：∠A＝∠D．（答案不唯一）
3．（2022•乐山）如图，B是线段AC的中点，AD∥BE，BD∥CE．求证：△ABD≌△BCE．
【解答】证明：∵点B为线段AC的中点，
∴AB＝BC，
∵AD∥BE，
∴∠A＝∠EBC，
∵BD∥CE，
∴∠C＝∠DBA，
在△ABD与△BCE中，
，
∴△ABD≌△BCE．（ASA）．
类型二 轴对称型
4．（2022•金华）如图，AC与BD相交于点O，OA＝OD，OB＝OC，不添加辅助线，判定△ABO≌△DCO的依据是（ ）
A．SSSB．SASC．AASD．HL
【答案】B
【解答】解：在△AOB和△DOC中，
，
∴△AOB≌△DOC（SAS），
故选：B．
5．（2020•永州）如图，已知AB＝DC，∠ABC＝∠DCB，能直接判断△ABC≌△DCB的方法是（ ）
A．SASB．AASC．SSSD．ASA
【答案】A
【解答】解：∵AB＝DC，∠ABC＝∠DCB，BC＝CB，
∴△ABC≌△DCB（SAS），
故选：A．
6．（2020•甘孜州）如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE≌△ACD的是（ ）
AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC
【答案】B
【解答】解：∵△ABC为等腰三角形，
∴∠ABC＝∠ACB，AB＝AC，
∴当AD＝AE时，则根据“SAS”可判断△ABE≌△ACD；
当∠AEB＝∠ADC，则根据“AAS”可判断△ABE≌△ACD；
当∠DCB＝∠EBC，则∠ABE＝∠ACD，根据“ASA”可判断△ABE≌△ACD．
故选：B．
7．（2021•济宁）如图，四边形ABCD中，∠BAC＝∠DAC，请补充一个条件 ，使△ABC≌△ADC．
【答案】AD＝AB（答案不唯一）
【解答】解：添加的条件是AD＝AB，
理由是：在△ABC和△ADC中
，
∴△ABC≌△ADC（SAS），
故答案为：AD＝AB（答案不唯一）．
8．（2022•广州）如图，点D，E在△ABC的边BC上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE．
【解答】证明：∵∠B＝∠C，
∴AB＝AC，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）．
9．（2020•柳州）如图，已知OC平分∠MON，点A、B分别在射线OM，ON上，且OA＝OB．
求证：△AOC≌△BOC．
【解答】证明：∵OC平分∠MON，
∴∠AOC＝∠BOC，
在△AOC和△BOC中，
，
∴△AOC≌△BOC（SAS）．
类型三 旋转型
考向1 共顶点旋转
10．（2021•哈尔滨）如图，△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE＝65°，则∠CAF的度数为（ ）
A．30°B．25°C．35°D．65°
【答案】B
【解答】解：∵△ABC≌△DEC，
∴∠ACB＝∠DCE，
∵∠BCE＝65°，
∴∠ACD＝∠BCE＝65°，
∵AF⊥CD，
∴∠AFC＝90°，
∴∠CAF+∠ACD＝90°，
∴∠CAF＝90°﹣65°＝25°，
故选：B．
11．（2021•齐齐哈尔）如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是 ．（只需写出一个条件即可）
【答案】∠B＝∠E或∠C＝∠D或AB＝AE
【解答】解：∵∠1＝∠2，
∴∠1+∠BAD＝∠2+∠BAD，
即∠BAC＝∠EAD，
∵AC＝AD，
∴当添加∠B＝∠E时，可根据“AAS”判断△ABC≌△AED；
当添加∠C＝∠D时，可根据“ASA”判断△ABC≌△AED；
当添加AB＝AE时，可根据“SAS”判断△ABC≌△AED．
故答案为∠B＝∠E或∠C＝∠D或AB＝AE．
12．（2022•宁夏）如图，AC，BD相交于点O，OB＝OD，要使△AOB≌△COD，添加一个条件是 .（只写一个）
【答案】OA＝OC（答案不唯一）
【解答】解：∵OB＝OD，∠AOB＝∠COD，OA＝OC，
∴△AOB≌△COD（SAS），
∴要使△AOB≌△COD，添加一个条件是OA＝OC，
故答案为：OA＝OC（答案不唯一）．
13．（2022•牡丹江）如图，CA＝CD，∠ACD＝∠BCE，请添加一个条件 ，使△ABC≌△DEC．
【答案】CB＝CE（答案不唯一）
【解答】解：∵∠ACD＝∠BCE，
∴∠ACD+∠ACE＝∠BCE+∠ACE，
∴∠DCE＝∠ACB，
∵CA＝CD，CB＝CE，
∴△ABC≌△DEC（SAS），
故答案为：CB＝CE（答案不唯一）．
14．（2021•宜宾）如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．
求证：△AOB≌△COD．
【解答】证明：∵∠AOC＝∠BOD，
∴∠AOC﹣∠AOD＝∠BOD﹣∠AOD，
即∠COD＝∠AOB，
在△AOB和△COD中，
，
∴△AOB≌△COD（SAS
考向2 不共顶点旋转
1．（2021•台湾）已知△ABC与△DEF全等，A、B、C的对应点分别为D、E、F，且E点在AC上，B、F、C、D四点共线，如图所示．若∠A＝40°，∠CED＝35°，则下列叙述何者正确？（ ）
A．EF＝EC，AE＝FCB．EF＝EC，AE≠FC
C．EF≠EC，AE＝FCD．EF≠EC，AE≠FC
【答案】B
【解答】解：∵△ABC≌△DEF，
∴∠A＝∠D＝40°，AC＝DF，∠ACB＝∠DFE，
∵∠ACB＝∠DFE，
∴EF＝EC．
∵∠CED＝35°，∠D＝40°，
∴∠D＞∠CED．
∴CE＞CD．
∵AC＝DF，
∴AC﹣CE＜DF﹣CD，即AE＜FC．
∴AE≠FC．
∴EF＝EC，AE≠FC．
故选：B．
类型四 三垂直型
16．（2022•益阳）如图，在Rt△ABC中，∠B＝90°，CD∥AB，DE⊥AC于点E，且CE＝AB．求证：△CED≌△ABC．
【解答】证明：∵DE⊥AC，∠B＝90°，
∴∠DEC＝∠B＝90°，
∵CD∥AB，
∴∠A＝∠DCE，
在△CED和△ABC中，
，
∴△CED≌△ABC（ASA）．
17．（2022•铜仁市）如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB＝CD．求证：△ABC≌△CDE．
【解答】证明：∵AB⊥BD，ED⊥BD，AC⊥CE，
∴∠B＝∠D＝∠ACE＝90°，
∴∠DCE+∠DEC＝90°，∠BCA+∠DCE＝90°，
∴∠BCA＝∠DEC，
在△ABC和△CDE中，
，
∴△ABC≌△CDE（AAS）．
其他类型
18．（2021•陕西）如图，BD∥AC，BD＝BC，点E在BC上，且BE＝AC．求证：∠D＝∠ABC．
【答案】略
【解答】证明：∵BD∥AC，
∴∠ACB＝∠EBD，
在△ABC和△EDB中，
，
∴△ABC≌△EDB（SAS），
∴∠ABC＝∠D．
19.（2020•温州）如图，在△ABC和△DCE中，AC＝DE，∠B＝∠DCE＝90°，点A，C，D依次在同一直线上，且AB∥DE．
（1）求证：△ABC≌△DCE．
（2）连接AE，当BC＝5，AC＝12时，求AE的长．
【答案】（1）略 （2）13
【解答】证明：（1）∵AB∥DE，
∴∠BAC＝∠D，
又∵∠B＝∠DCE＝90°，AC＝DE，
∴△ABC≌△DCE（AAS）；
（2）∵△ABC≌△DCE，
∴CE＝BC＝5，
∵∠ACE＝90°，
∴AE＝＝＝13．
命题点2 全等三角形的实际应用
20．（2021•盐城）工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别截取OC＝OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线．这里构造全等三角形的依据是（ ）
A．SASB．ASAC．AASD．SSS
【答案】D
【解答】解：在△COM和△DOM中
，
所以△COM≌△DOM（SSS），
所以∠COM＝∠DOM，
即OM是∠AOB的平分线，
故选：D．
21．（2021•柳州）如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB，连接DE，那么量出DE的长就是A、B的距离，为什么？请结合解题过程，完成本题的证明．
证明：在△DEC和△ABC中，
，
∴△DEC≌△ABC（SAS），
∴ ．
【答案】CA，∠DCE＝∠ACB，CB，DE＝AB．
【解答】证明：在△DEC和△ABC中，
，
∴△DEC≌△ABC（SAS），
∴DE＝AB．
故答案为：CA，∠DCE＝∠ACB，CB，DE＝AB．