

所属成套资源:中考数学第一轮专题复习真题分点透练(全国通用)(原卷版+解析)
中考数学第一轮专题复习真题分点透练(全国通用)第二十三讲尺规作图(原卷版+解析)
展开
这是一份中考数学第一轮专题复习真题分点透练(全国通用)第二十三讲尺规作图(原卷版+解析),共33页。
1.(2022•德州)在△ABC中,根据下列尺规作图的痕迹,不能判断AB与AC大小关系的是( )
A.B.
C.D.
2.(2022•益阳)如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A.I到AB,AC边的距离相等
B.CI平分∠ACB
C.I是△ABC的内心
D.I到A,B,C三点的距离相等
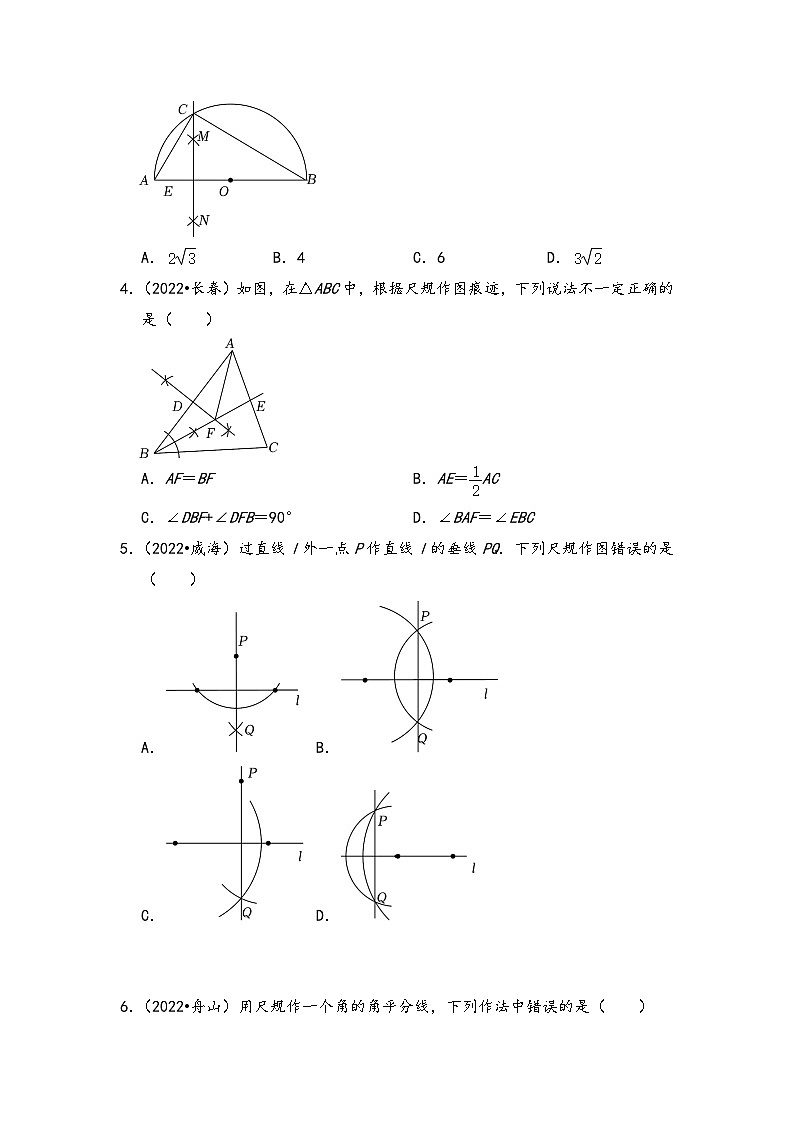
3.(2022•盘锦)如图,线段AB是半圆O的直径.分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线MN,交半圆O于点C,交AB于点E,连接AC,BC,若AE=1,则BC的长是( )
A.B.4C.6D.
4.(2022•长春)如图,在△ABC中,根据尺规作图痕迹,下列说法不一定正确的是( )
A.AF=BFB.AE=AC
C.∠DBF+∠DFB=90°D.∠BAF=∠EBC
5.(2022•威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.
C.D.
6.(2022•舟山)用尺规作一个角的角平分线,下列作法中错误的是( )
A.B.
C.D.
类型二 根据作图步骤进行计算、证明或结论判断
7.(2022•淄博)如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.若CD=3,则BD的长为( )
A.4B.5C.6D.7
8.(2022•黄石)如图,在△ABC中,分别以A,C为圆心,大于AC长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若AE=2cm,△ABD的周长为11cm,则△ABC的周长为( )
A.13cmB.14cmC.15cmD.16cm
9.(2022•资阳)如图所示,在△ABC中,按下列步骤作图:
第一步:在AB、AC上分别截取AD、AE,使AD=AE;
第二步:分别以点D和点E为圆心、适当长(大于DE的一半)为半径作圆弧,两弧交于点F;
第三步:作射线AF交BC于点M;
第四步:过点M作MN⊥AB于点N.
下列结论一定成立的是( )
A.CM=MN B.AC=AN C.∠CAM=∠BAM D.∠CMA=∠NMA
10.(2022•锦州)如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为( )
A.B.C.D.
11.(2022•聊城)如图,△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠BAQ=40°B.DE=BDC.AF=ACD.∠EQF=25°
12.(2022•百色)如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( )
A.∠B=45°B.AE=EBC.AC=BCD.AB⊥CD
13.(2022•营口)如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则以下推断错误的是( )
A.BD=BCB.AD=BDC.∠ADB=108°D.CD=AD
14.(2022•鄂州)如图,直线l1∥l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10°B.15°C.20°D.30°
15.(2022•枣庄)如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D为圆心,以大于BD的长为半径作弧,两弧相交于点E和F;②作直线EF分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN= .
16.(2022•辽宁)如图,在△ABC中,AB=AC,∠B=54°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是 .
类型三 依据要求直接作图
17.(2022•淮安)如图,已知线段AC和线段a.
(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
①作线段AC的垂直平分线l,交线段AC于点O;
②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.
(2)当AC=4,a=2时,求(1)中所作矩形ABCD的面积.
18.(2022•襄阳)如图,在△ABC中,AB=AC,BD是△ABC的角平分线.
(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);
(2)求证:AD=AE.
19.(2022•宁夏)如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.
(1)用尺规作∠ABC的角平分线,交CD于点E;
(不写作法,保留作图痕迹)
(2)连接AE.求证:四边形ABCE是菱形.
20.(2022•赤峰)如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.
(1)作BC的垂直平分线,分别交AB、BC于点D、H;
(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接CD,求△BCD的周长.
类型四 转化类作图
21.(2022•陕西)如图,已知△ABC,CA=CB,∠ACD是△ABC的一个外角.
请用尺规作图法,求作射线CP,使CP∥AB.(保留作图痕迹,不写作法)
命题点2 无刻度直尺作图
类型一 网格中作图
22.(2022•长春)图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)网格中△ABC的形状是 ;
(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;
(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;
(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.
23.(2022•江西)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作∠ABC的角平分线;
(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.
类型二 根据图形性质作图
24.(2022•湖北)已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;
(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.
25.(2022•无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且CD⊥AD;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若∠B=60°,AB=2,BC=3,则四边形ABCD的面积为 .
26.(2022•绥化)已知:△ABC.
(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)
(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.
27.(2022•扬州)【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
第二十三讲 尺规作图
命题点1 五种基本尺规作图
类型一 判定作图结果
1.(2022•德州)在△ABC中,根据下列尺规作图的痕迹,不能判断AB与AC大小关系的是( )
A.B.
C.D.
【答案】D
【解答】解:A.由作图痕迹,在AC上截取线段等于AB,则AC>AB,所以A选项不符合题意;
B.由作图痕迹,在AB上延长线上截取线段等于AC,则AC>AB,所以B选项不符合题意;
C.由作图痕迹,作BC的垂直平分线把AC分成两线段,则AC>AB,所以C选项不符合题意;
D.由作图痕迹,作AC的垂直平分线,则BC>AB,所以D选项符合题意.
故选:D.
2.(2022•益阳)如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A.I到AB,AC边的距离相等
B.CI平分∠ACB
C.I是△ABC的内心
D.I到A,B,C三点的距离相等
【答案】D
【解答】解:由作图可知,AE是∠BAC的平分线,
∴I到AB,AC边的距离相等,故选项A正确,不符合题意;
∵BD平分∠ABC,三角形三条角平分线交于一点,
∴CI平分∠ACB,故选项B正确,不符合题意;
I是△ABC的内心,故选项C正确,不符合题意,
∴I到AB,AC,BC的距离相等,不是到A,B,C三点的距离相等,故选项D错误,符合题意;
故选:D.
3.(2022•盘锦)如图,线段AB是半圆O的直径.分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线MN,交半圆O于点C,交AB于点E,连接AC,BC,若AE=1,则BC的长是( )
A.B.4C.6D.
【答案】A
【解答】解:如图,连接OC.
根据作图知CE垂直平分AO,
∴AC=OC,AE=OE=1,
∴OC=OB=AO=AE+EO=2,
∴AC=OC=AO=AE+EO=2,
即AB=AO+BO=4,
∵线段AB是半圆O的直径,
∴∠ACB=90°,
在Rt△ACB中,根据勾股定理得,,
故选A.
4.(2022•长春)如图,在△ABC中,根据尺规作图痕迹,下列说法不一定正确的是( )
A.AF=BFB.AE=AC
C.∠DBF+∠DFB=90°D.∠BAF=∠EBC
【答案】B
【解答】解:由图中尺规作图痕迹可知,
BE为∠ABC的平分线,DF为线段AB的垂直平分线.
由垂直平分线的性质可得AF=BF,
故A选项不符合题意;
∵DF为线段AB的垂直平分线,
∴∠BDF=90°,
∴∠DBF+∠DFB=90°,
故C选项不符合题意;
∵BE为∠ABC的平分线,
∴∠ABF=∠EBC,
∵AF=BF,
∴∠ABF=∠BAF,
∴∠BAF=∠EBC,
故D选项不符合题意;
根据已知条件不能得出AE=AC,
故B选项符合题意.
故选:B.
5.(2022•威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.
C.D.
【答案】C
【解答】解:选项A,连接PA,PB,QA,QB,
∵PA=PB,
∴点P在线段AB的垂直平分线上,
∵QA=QB,
∴点Q在线段AB的垂直平分线上,
∴PQ⊥l,故此选项不符合题意;
选项B,连接PA,PB,QA,QB,
∵PA=QA,
∴点A在线段PQ的垂直平分线上,
∵PB=QB,
∴点B在线段PQ的垂直平分线上,
∴PQ⊥l,故此选项不符合题意;
选项C,无法证明PQ⊥l,故此选项符合题意;
选项D,连接PA,PB,QA,QB,
∵PA=QA,
∴点A在线段PQ的垂直平分线上,
∵PB=QB,
∴点B在线段PQ的垂直平分线上,
∴PQ⊥l,故此选项不符合题意;
故选:C.
6.(2022•舟山)用尺规作一个角的角平分线,下列作法中错误的是( )
A.B.
C.D.
【答案】D
【解答】解:由图可知,选项A、B、C中的线都可以作为角平分线;
选项D中的图作出的是平行四边形,不能保证角中间的线是角平分线,
故选:D.
类型二 根据作图步骤进行计算、证明或结论判断
7.(2022•淄博)如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.若CD=3,则BD的长为( )
A.4B.5C.6D.7
【答案】C
【解答】解:连接AD,如图,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
由作法得DE垂直平分AC,
∴DA=DC=3,
∴∠DAC=∠C=30°,
∴∠BAD=120°﹣30°=90°,
在Rt△ABD中,∵∠B=30°,
∴BD=2AD=6.
故选:C.
8.(2022•黄石)如图,在△ABC中,分别以A,C为圆心,大于AC长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若AE=2cm,△ABD的周长为11cm,则△ABC的周长为( )
A.13cmB.14cmC.15cmD.16cm
【答案】C
【解答】解:由作法得MN垂直平分AC,
∴DA=DC,AE=CE=2cm,
∵△ABD的周长为11cm,
∴AB+BD+AD=11cm,
∴AB+BD+DC=11cm,即AB+BC=11cm,
∴△ABC的周长=AB+BC+AC=11+2×2=15(cm).
故选:C.
9.(2022•资阳)如图所示,在△ABC中,按下列步骤作图:
第一步:在AB、AC上分别截取AD、AE,使AD=AE;
第二步:分别以点D和点E为圆心、适当长(大于DE的一半)为半径作圆弧,两弧交于点F;
第三步:作射线AF交BC于点M;
第四步:过点M作MN⊥AB于点N.
下列结论一定成立的是( )
A.CM=MN B.AC=AN C.∠CAM=∠BAM D.∠CMA=∠NMA
【答案】C
【解答】解:由题意可知,AM平分∠CAB,
∵∠C不一定等于90°,∴CM≥MN,因此A选项不符合题意;
∵∠C不一定等于90°,∴AC不一定等于AN,因此B选项不符合题意;
∵AM平分∠CAB,∴∠CAM=∠BAM,因此C选项符合题意;
∵∠C不一定等于90°,∴∠CMA不一定等于∠NMA,因此D选项不符合题意.
故选:C.
10.(2022•锦州)如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为( )
A.B.C.D.
【答案】D
【解答】解:设MN与AC的交点为O,
∵四边形ABCD为矩形,
∴∠ADC=90°,AB=DC=6,BC=AD=8,
∴△ADC为直角三角形,
∵CD=6,AD=8,
∴,,
又由作图知MN为AC的垂直平分线,
∴∠MOA=90°,,
在Rt△AOE中,,
∵cs∠CAD=cs∠EAO,
∴,
∴.
故选:D.
11.(2022•聊城)如图,△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠BAQ=40°B.DE=BDC.AF=ACD.∠EQF=25°
【答案】D
【解答】解:A.由作图可知,AQ平分∠BAC,
∴∠BAP=∠CAP=∠BAC=40°,
故选项A正确,不符合题意;
B.由作图可知,MQ是BC的垂直平分线,
∴∠DEB=90°,
∵∠B=30°,
∴DE=BD,
故选项B正确,不符合题意;
C.∵∠B=30°,∠BAP=40°,
∴∠AFC=70°,
∵∠C=70°,
∴AF=AC,
故选项C正确,不符合题意;
D.∵∠EFQ=∠AFC=70°,∠QEF=90°,
∴∠EQF=20°;
故选项D错误,符合题意.
故选:D.
12.(2022•百色)如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( )
A.∠B=45°B.AE=EBC.AC=BCD.AB⊥CD
【答案】A
【解答】解:由作图痕迹得CD垂直平分AB,
AE=BE,AC=BC,AB⊥CD.
所以A选项不一定成立,B、C、D选项成立.
故选:A.
13.(2022•营口)如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则以下推断错误的是( )
A.BD=BCB.AD=BDC.∠ADB=108°D.CD=AD
【答案】D
【解答】解:在△ABC中,
∵AB=AC,
∴∠ABC=∠ACB.
∵∠A=36°,
∴∠ABC=∠C=(180°﹣36°)=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°.
∴∠ABD=∠A.
∴AD=BD.故选项B正确;
∵∠BDC=∠A+∠ABD=72°.
∴∠C=∠BDC.
∴BD=BC.故选项A正确;
∵∠BDC=72°,
∴∠ADB=108°.故选项C正确;
在△BCD与△ACB中,
∵∠CBD=∠A=36°,∠C为公共角.
∴△BCD∽△ACB.
∴.
∴BC2=AC•CD.
∵BC=BD=AD,AC=AD+CD.
∴AD2=(AD+CD)•CD.整理得,CD2﹣AD•CD﹣AD2=0.
解得,CD=AD.
∴CD≠AD.故选项D错误.
故选:D.
14.(2022•鄂州)如图,直线l1∥l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10°B.15°C.20°D.30°
【答案】B
【解答】解:由题意可得AC=BC,
∴∠CAB=∠CBA,
∵∠BCA=150°,∠BCA+∠CAB+∠CBA=180°,
∴∠CAB=∠CBA=15°,
∵l1∥l2,
∴∠1=∠CBA=15°.
故选:B.
15.(2022•枣庄)如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D为圆心,以大于BD的长为半径作弧,两弧相交于点E和F;②作直线EF分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN= .
【答案】2
【解答】解:如图,连接BM.
由作图可知MN垂直平分线段BD,
∴BM=DM=5,
∵四边形ABCD是矩形,
∴∠C=90°,CD∥AB,
∴BC===4,
∴BD===4,
∴OB=OD=2,
∵∠MOD=90°,
∴OM===,
∵CD∥AB,
∴∠MDO=∠NBO,
在△MDO和△NBO中,
,
∴△MDO≌△BNO(ASA),
∴OM=ON=,
∴MN=2.
故答案为:2.
16.(2022•辽宁)如图,在△ABC中,AB=AC,∠B=54°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是 .
【答案】18°
【解答】解:由作图可得,CF⊥AB于F,
∴∠BFC=90°,
∴∠BCF=90°﹣∠B=36°,
又∵AB=AC,∠B=54°,
∴∠ACB=∠B=54°,
∴∠ACF=54°﹣36°=18°,
故答案为:18°
类型三 依据要求直接作图
17.(2022•淮安)如图,已知线段AC和线段a.
(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
①作线段AC的垂直平分线l,交线段AC于点O;
②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.
(2)当AC=4,a=2时,求(1)中所作矩形ABCD的面积.
【解答】解:(1)①如图,直线l即为所求.
②如图,矩形ABCD即为所求.
(2)∵四边形ABCD为矩形,
∴∠ABC=90°,
∵a=2,
∴AB=CD=2,
∴BC=AD===,
∴矩形ABCD的面积为AB•BC=2×=.
18.(2022•襄阳)如图,在△ABC中,AB=AC,BD是△ABC的角平分线.
(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);
(2)求证:AD=AE.
【解答】(1)解:如图所示.
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD是∠ABC的角平分线,CE是∠ABC的角平分线,
∴∠ABD=∠ACE,
∵AB=AC,∠A=∠A,
∴△ACE≌△ABD(ASA),
∴AD=AE.
19.(2022•宁夏)如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.
(1)用尺规作∠ABC的角平分线,交CD于点E;
(不写作法,保留作图痕迹)
(2)连接AE.求证:四边形ABCE是菱形.
【解答】(1)解:如图所示.
(2)证明:∵BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∵AB∥CD,
∴∠ABE=∠BEC,
∴∠CBE=∠BEC,
∴BC=EC,
∵AB=BC,
∴AB=EC,
∴四边形ABCE为平行四边形,
∵AB=BC,
∴四边形ABCE为菱形.
20.(2022•赤峰)如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.
(1)作BC的垂直平分线,分别交AB、BC于点D、H;
(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接CD,求△BCD的周长.
【解答】解:(1)如图,DH为所作;
(2)∵DH垂直平分BC,
∴DC=DB,
∴∠B=∠DCB,
∵∠B+∠A=90°,∠DCB+∠DCA=90°,
∴∠A=∠DCA,
∴DC=DA,
∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13.
类型四 转化类作图
21.(2022•陕西)如图,已知△ABC,CA=CB,∠ACD是△ABC的一个外角.
请用尺规作图法,求作射线CP,使CP∥AB.(保留作图痕迹,不写作法)
【解答】解:如图,射线CP即为所求.
命题点2 无刻度直尺作图
类型一 网格中作图
22.(2022•长春)图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)网格中△ABC的形状是 ;
(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;
(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;
(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.
【解答】解:(1)∵AC==,AB==2,BC=5,
∴AC2+AB2=BC2,
∴∠BAC=90°,
∴△ABC是直角三角形;
故答案为:直角三角形;
(2)如图①中,点D,点D′,点D″即为所求;
(3)如图②中,点E即为所求;
(4)如图③,点P,点Q即为所求.
23.(2022•江西)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作∠ABC的角平分线;
(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.
【解答】解:(1)如图1中,射线BP即为所求;
(2)如图2中,直线l或直线l′即为所求.
类型二 根据图形性质作图
24.(2022•湖北)已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;
(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.
【解答】解:(1)如图1中,直线m即为所求;
(2)如图2中,直线n即为所求;
25.(2022•无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且CD⊥AD;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若∠B=60°,AB=2,BC=3,则四边形ABCD的面积为 .
【解答】解:(1)如图1中,点D即为所求;
(2)过点A作AH⊥BC于点H.
在Rt△ABH中,AB=2,∠B=60°,
∴BH=AB•cs60°=1,AH=AB•sin60°=,
∴CH=BC﹣BH=2,
∵∠DAC=∠ACB,
∴AD∥BC,
∵AH⊥CB,CD⊥AD,
∴∠AHC=∠ADC=∠DCH=90°,
∴四边形AHCD是矩形,
∴AD=CH=2,
∴S四边形ABCD=×(2+3)×=,
故答案为:.
26.(2022•绥化)已知:△ABC.
(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)
(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.
【解答】解:(1)如图,点O即为所求;
(2)由题意,△ABC的面积=×14×1.3=9.1(cm2).
27.(2022•扬州)【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
【解答】解:【初步尝试】如图1,直线OP即为所求;
【问题联想】如图2,三角形MNP即为所求;
【问题再解】如图3中,即为所求.
相关试卷
这是一份第三讲 分式及其运算-备战中考数学第一轮专题复习真题分点透练(全国通用),文件包含第三讲分式及其运算解析版docx、第三讲分式及其运算原卷版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
这是一份第二十讲 圆的基本性质-备战中考数学第一轮专题复习真题分点透练(全国通用),文件包含第二十讲圆的基本性质解析版docx、第二十讲圆的基本性质原卷版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
这是一份第十三讲 角、相交线与平行线-备战中考数学第一轮专题复习真题分点透练(全国通用),文件包含第十三讲角相交线与平行线解析版docx、第十三讲角相交线与平行线原卷版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。









