苏科版八年级上册6.2 一次函数课后测评

这是一份苏科版八年级上册6.2 一次函数课后测评，文件包含第六章一次函数知识归纳+题型突破原卷版docx、第六章一次函数知识归纳+题型突破解析版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
结合情境理解一次函数含义，辨别一次函数正比例的区别与联系。
学会待定系数法求函数解析式，从图像角度理解函数图像性质，
培养数形结合的思想，综合解决函数问题。
一、函数的概念
1、函数概念：一般地，在一个变化过程中的两个变量x和y，如果对于x的每一个值，y都有唯一的值与它对应，那么我们称y是x的函数，x是自变量．
2、函数表达形式：①列表；②函数表达式；③函数图像
二、一次函数、正比例函数的概念
1、一次函数的概念：一般地，解析式形如（k，b是常数，且）的函数叫做一次函数．
2、正比例函数的概念：当时，是正比例函数．
3、待定系数法：先写出含有未知系数的函数表达式，再根据条件求出这些未知系数的值，从而确定函数表达式，这样的方法叫做待定系数法．
三、一次函数的图象与性质
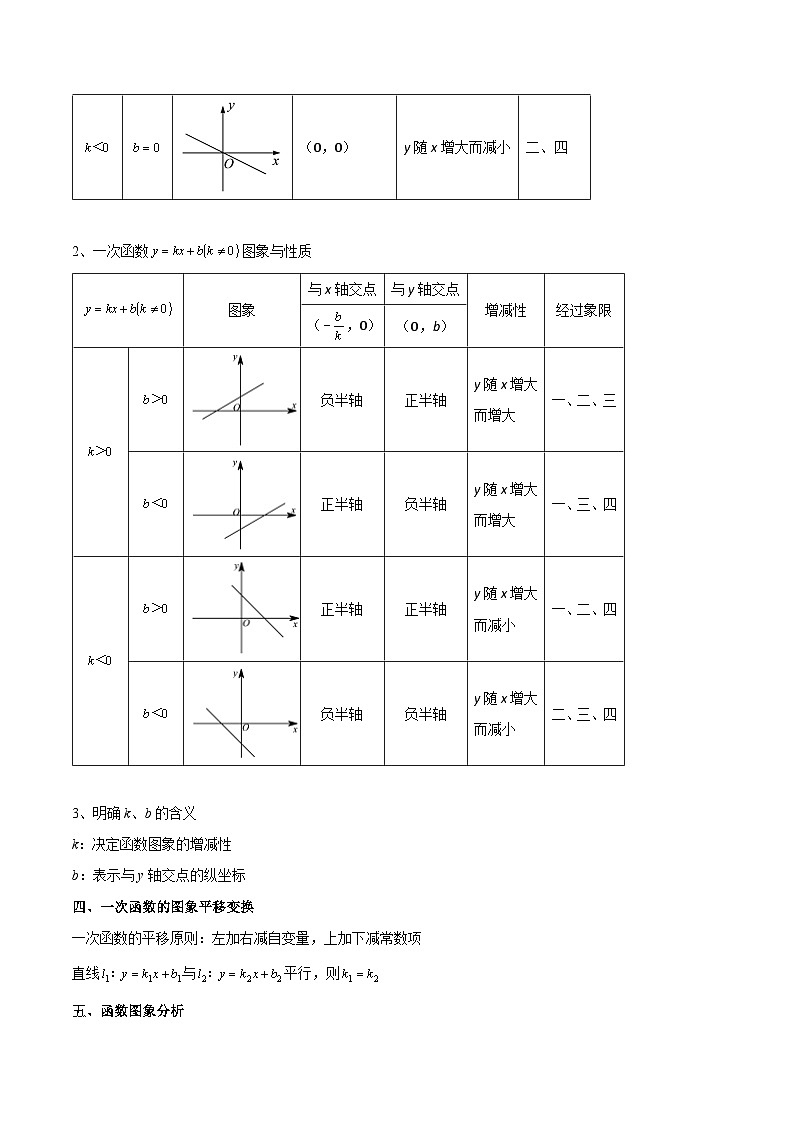
1、正比例函数图象与性质
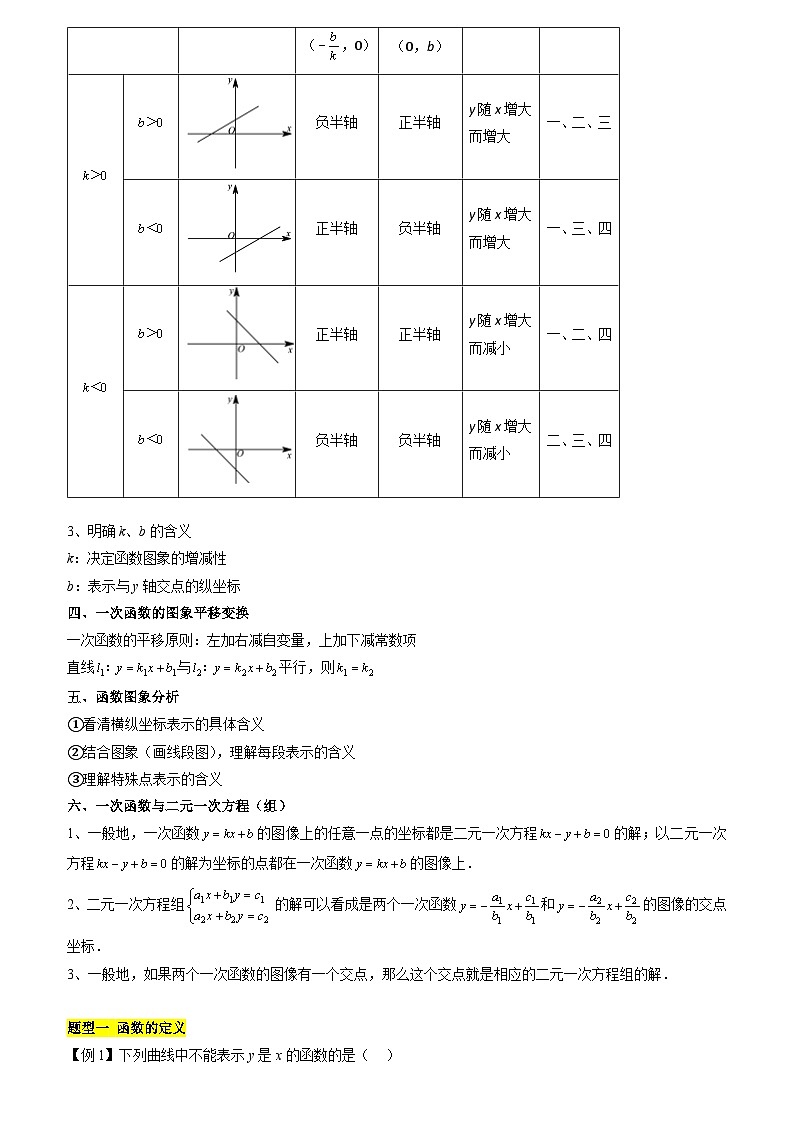
2、一次函数图象与性质
3、明确k、b的含义
k：决定函数图象的增减性
b：表示与y轴交点的纵坐标
四、一次函数的图象平移变换
一次函数的平移原则：左加右减自变量，上加下减常数项
直线与平行，则
五、函数图象分析
①看清横纵坐标表示的具体含义
②结合图象（画线段图），理解每段表示的含义
③理解特殊点表示的含义
六、一次函数与二元一次方程（组）
1、一般地，一次函数的图像上的任意一点的坐标都是二元一次方程的解；以二元一次方程的解为坐标的点都在一次函数的图像上．
2、二元一次方程组的解可以看成是两个一次函数和的图像的交点坐标．
3、一般地，如果两个一次函数的图像有一个交点，那么这个交点就是相应的二元一次方程组的解．
题型一 函数的定义
【例1】下列曲线中不能表示y是x的函数的是（ ）
A． B．
C． D．
【例2】下列各曲线中，能表示y是x的函数的是（ ）
A． B． C． D．
巩固训练
1．下列各图象中，y不是x的函数的是（ ）
A． B．
C． D．
2．下列图象中，表示y是x的函数的是（ ）
A． B． C． D
题型二 自变量范围
【例3】函数的自变量x的取值范围是（ ）
A．B．C．D．
【例4】若函数有意义，则自变量的取值范围在数轴上表示正确的是（ ）
A． B．
C． D．
【例5】函数的自变量取值范围是 ．
巩固训练
3．函数中自变量的取值范围是（ ）
A．B．C．D．
4．函数中，自变量的取值范围是 ．
5．函数的自变量x的取值范围是 ．
题型三 函数的解析式
【例6】某超市为客户提供某种水果同城配送服务，具体方案如下：若客户购买该水果不超过，单价为每千克20元；超过，超出部分的单价则为每千克15元．此外每次配送收取配送费10元．超市为同城某客户配送该水果，客户付款y（元），则y与x（）的关系式为 ．
【例7】汽车开始行驶时，油箱中有油30升，如果每小时耗油5升，那么油箱中的剩余油量（升）和工作时间（时）之间的函数关系式是 ．
巩固训练
6．一个水瓶中初始有水，每小时漏水，请写出水瓶中剩余水量单位：关于时间单位：的函数关系解析式是 ，其中自变量的取值范围是 ．
题型四 正比例（一次）函数定义
【例8】下列各点，在正比例函数的图象上的是（ ）
A．B．C．D．
【例9】已知函数．
(1)m为何值时，这个函数是一次函数；
(2)m为何值时，这个函数是正比例函数．
巩固训练
7．已知函数是一次函数，则m的值是 ．
8．若是关于x的一次函数，则m的值为 ．
9．若函数是关于的一次函数，则 ．
题型五 求一次函数自变量参数或函数值
【例10】已知直线与直线交于点，则代数式的值为（ ）
A．3B．2C．1D．0
【例11】已知函数，则当函数值时，自变量的值是 ．
【例12】在平面直角坐标系中，直线过点，则的值为 ．
巩固训练
10．已知直线经过，则的值为 ．
11．已知，和都在一次函数的图象上，若，则的值为 ．
12．已知为直线上的一点，若，满足，且，则的值是 ．
题型六 正比例函数图像和性质
【例13】若正比例函数（）经过点，，则该正比例函数的解析式为
【例14】如图，在图象上有一点A，若A点的坐标为，O为原点．则的长为 ．

【例15】下图表示一辆汽车行驶的路程与耗油量的关系．

（1）这辆汽车行驶的路程与耗油量之间成 比例关系．
（2）如果汽车行驶500千米，耗油 升．
巩固训练
13．如图，正比例函数在同一平面直角坐标系中的图象如图所示．则比例系数k，m，n的大小关系是 ．（按从大到小的顺序用“＞”连接）

14．正比例函数y＝的图象经过的象限是（ ）
A．第一、三象限B．第二、四象限
C．第三、四象限D．第一、二象限
15．如图，三个正比例函数的图象对应的解析式为①，②，③，则a、b、c的大小关系是（ ）

A． B． C． D．
16．当时，正比例函数的图象大致是（ ）
A． B． C． D．
17．若一个正比例函数的图象经过点，则它的表达式为（ ）
A． B． C．D．
18．关于正比例函数，下列结论不正确的是（ ）
A．图象经过原点B．y随x的增大而减小
C．点在函数的图象上D．图象经过二、四象限
题型六 一次函数值大小比较
【例16】若点，都在直线上，则与的大小关系是（ ）
A．B．C．D．无法比较大小
【例17】已知，是一次函数y图象上的两个点，则，的大小关系是( )
A．B．C．D．不能确定
巩固训练
19．已知点，在一次函数的图象上，则（ ）
A．B．C．D．无法确定
20．一次函数上有两个点A，B，且，则m，n的大小关系为m n．
21．一次函数的图像过点，，，则，，的大小关系为 ．（用“”连接）
题型七 一次函数与坐标轴交点问题
【例18】一次函数与轴交点的坐标为 ，与轴交点的坐标为 ．
【例19】函数的图像与x轴交点坐标为 ．
巩固训练
22．直线与x轴的交点坐标是 ；与y轴的交点坐标是 ；与坐标轴围成的三角形面积为 ．
23．已知为第二象限内的点，则一次函数的图象大致是（ ）
A． B． C． D．
题型八 一次函数象限与增减性
【例20】下列关于一次函数的说法中，正确的是（ ）
A．图象经过第一、二、四象限B．y随x的增大而减小
C．当时，D．图象与y轴交于点
【例21】对于一次函数的图象及性质，下列结论正确的是（ ）
A．图象与的图象平行B．随的增大而增大
C．图象经过第一、二、三象限D．图象必过点
【例22】若一次函数与坐标轴围成的三角形的面积为，则下列说法正确的是（ ）
A．的值为或B．的值随的增大而增大
C．该函数图象经过第一、二、三象限D．在的范围内，的最大值为
巩固训练
24．一次函数的图象如图所示，则下列结论正确的是（ ）

A．当时，B．当时，C．当时，D．当时，
25．对于函数，下列结论正确的是（ ）
A．它的图象必经过点B．它的图象经过第一、二、三象限
C．当时，D．y的值随 x值的增大而增大
26．两个一次函数、，它们在同一坐标系中的图象可能是图中的（ ）
A． B．
C． D．
27．一次函数的图象经过的象限为（ ）
A．第一、三、四象限B．第一、二、三象限
C．第二、三、四象限D．第一、二、四象限
题型九 一次函数图像平移问题
【例23】把直线向左平移1个单位长度，再向上平移2个单位长度，则平移后所得直线的解析式为（ ）
A．B．C．D．
【例24】函数图象向右平移2个单位后，对应函数为（ ）
A．B．
C．D．
【例25】在平面直角坐标系中，若将直线向上平移个单位长度得到直线，则的值为（ ）
A．4B．C．2D．
巩固训练
28．函数的图象可由函数的图象沿y轴（ ）单位得到．
A．向上平移5个B．向下平移5个C．向左平移5个D．向右平移5个
29．将直线向左平移3个单位，向上平移2个单位后得到的直线是（ ）
A．B．C．D．
30．直线 向上平移m个单位长度，得到直线，则 .
题型十 一次函数的实际应用
【例26】某草莓种植大户，今年从草莓上市到销售完需要20天，售价为15元/千克，成本y（元/千克）与第x天成一次函数关系，当时，，当时，．
(1)求成本y（元/千克）与第x天的函数关系式并写出自变量x的取值范围；
(2)求第几天每千克的利润w（元）最大？最大利润是多少？（利润=售价-成本）
【例27】为了响应节能减排的号召，推动绿色生活方式，某品牌汽车店准备购进型和型两种不同型号的电动汽车共辆进行销售．
(1)如果该店购进辆两种型号的电动汽车所花费成本为万元，那么购进、两种型号的电动汽车各多少辆？
(2)如果为了保证该店购进的型电动汽车不少于型电动汽车的倍，那么辆电动汽车全部售出后，求购进多少辆型电动汽车可使店销售的利润最大，最大利润是多少？
(3)实际进货时，厂家对型电动汽车的成本价下调万元，若该店保持这两种型号电动汽车的售价不变，并且无论该店如何进货这辆电动汽车的销售利润不变，求的值．
【例28】为进行垃圾分类，我校准备购买，两种型号的垃圾箱，通过市场调研发现：购买1个型垃圾箱和2个型垃圾箱共需340元；购买5个型垃圾箱和2个型垃圾箱共需540元．
(1)求每个型垃圾箱和型垃圾箱各多少元？
(2)若需要购买，两种型号的垃圾箱共30个，其中购买型垃圾箱不超过15个，当购买型垃圾箱多少个时总花费（元）最少，最少费用是多少？
【例29】甲、乙两人同时从同一地点向目的地出发，甲、乙两人相对于出发地的距离（）与时间（）之间的关系如图所示．

(1)甲、乙两人的平均速度分别是多少？
(2)试分别确定甲、乙两人相对于出发地的距离（）与时间（）之间的关系式？
(3)3分钟时，甲、乙两人之间的距离是多少米？
【例30】李老师驱车从淮安回南京，上午8：00进入淮安高速入口，设在高速上行驶时间为，离南京高速出口的路程为，图中的折线表示与之间的函数关系，结合图象，解决下列问题：

(1)求线段对应的函数表达式及点的坐标；
(2)李老师说：“我在高速公路上，有一段连续恰好走了．”你认为有可能吗？若有，请求出这的起止时间；若没有，请说明理由．
巩固训练
31．某校计划送370名师生（其中学生362人、教师8人）到全国中小学生研学实践教育基地之一的澄江化石地世界自然遗产博物馆进行科普研学活动．现有甲、乙两种大客车，甲客车每辆可坐35人，乙客车每辆可坐50人，租用一辆甲客车和一辆乙客车共需700元，租用3辆甲客车和2辆乙客车共需1700元．
(1)租用甲、乙两种客车每辆各需多少元？
(2)要使每辆客车上至少要有1名教师，所有参与活动的师生都有车坐，则租用客车总数为8辆，设租用辆甲客车，租车的总费用为元，则共有几种不同的租车方案？哪种方案租车的总费用最少？
32．超市在周年庆期间，计划对某种商品进行促销活动，该超市预计分三个批次从生产厂家购进该商品20000件．这三个批次商品的进价如表所示：
若购买第二批次商品的数量是第一批次的2倍，设购进第一批次商品x件，该超市购进该商品的总费用为y元．
(1)请求出y与x的函数关系式；
(2)已知该商品的生产厂家能提供的第一批次商品的数量不大于第三批次商品的数量，当第一批次商品购进多少件时购买三个批次商品的总费用最少？并求最少总费用．
33．甲、乙两地相距，现有一辆汽车从乙地出发，以的速度向甲地行驶．设表示汽车行驶的时间，表示汽车与甲地的距离．
(1)写出y与x之间的关系式，并判断y是否为x的一次函数；
(2)当时，求y的值．
题型十一 一次函数与二元一次方程组
【例31】如图，根据函数图象回答问题：方程组的解为 ．

【例32】如图，直线与直线：交于点，则方程组的解是（ ）

A．B．C．D．
巩固训练
34．如图，已知函数和的图象交于点P，点P的横坐标为2，则关于x，y的方程组的解是 ．
35．已知关于x，y的方程组
(1)当k，b为何值时，方程组有唯一一组解；
(2)当k，b为何值时，方程组有无数组解；
(3)当k，b为何值时，方程组无解．
题型十二 一次函数与坐标轴交点及面积问题
【例33】如图，直线：和直线与轴分别相交于，两点，且两直线相交于点，直线与轴相交于点，．
(1)求点的坐标及直线的函数表达式；
(2)求的面积；
(3)试探究在轴上是否存在点，使得为等腰三角形，若存在，请直接写出点的坐标；若不存在，请说明理由．
巩固训练
36．如图，一次函数的图像为直线，经过和两点．一次函数的图像为直线，与轴交于点，直线，交于点．
(1)求一次函数的表达式；
(2)求点的坐标；
(3)求的面积．
37．如图，已知直线的解析式为，直线的解析式为：，与轴交于点，与交于点．

(1)求k，b的值；
(2)求三角形的面积．
题型十三 一次函数与一元一次不等式
【例34】一次函数和的图象如图所示，其交点为，则不等式的解集在数轴上表示正确的是（ ）
A．B．
C．D．
【例35】如图，已知正比例函数的图象和一次函数的图象交于点，则关于x的不等式的解集是（ ）

A．B．C．D．
【例36】在平面直角坐标系中，直线与y轴交于点A．
(1)求点A的坐标；
(2)将点A向右平移2个单位恰好落在直线上，点在直线上，点在直线上．若，求m的取值范围．
巩固训练
38．一次函数与的图象如图所示，则的解集是（ ）
A．B．C．D．
39．如图，在同一坐标系中一次函数和的图象分别与x轴交于A，B两点，两直线交于点C．已知点，．观察图象并回答下列问题：
(1)直按写出关于x的不等式组解集是______；
(2)若点C坐标为，
①关于x的不等式的解集是______；
②求的面积为______．
图象
与坐标轴交点
增减性
经过象限
（0，0）
y随x增大而增大
一、三
（0，0）
y随x增大而减小
二、四
图象
与x轴交点
与y轴交点
增减性
经过象限
（，0）
（0，b）
负半轴
正半轴
y随x增大而增大
一、二、三
正半轴
负半轴
y随x增大而增大
一、三、四
正半轴
正半轴
y随x增大而减小
一、二、四
负半轴
负半轴
y随x增大而减小
二、三、四
成本价（万元/辆）
售价（万元/辆）
型
型
批次
一
二
三
进价（元/件）
30
35
40