高考数学大一轮复习精讲精练(新高考地区)4.5解三角形6大常考题型(精讲)(原卷版+解析)

这是一份高考数学大一轮复习精讲精练(新高考地区)4.5解三角形6大常考题型(精讲)(原卷版+解析)，共26页。

【知识必备】
1．正弦定理、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.三角形面积公式：
S△ABC＝eq \f(1,2) ah(h表示边a上的高) ；
S△ABC＝eq \f(1,2)absin C＝eq \f(1,2)bcsin A＝eq \f(1,2)acsin B；
3.解三角形多解情况
在△ABC中，已知a，b和A时，解的情况如下：
4.实际应用
（1）仰角和俯角
在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．
（2）方位角
从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．
（3）方向角：相对于某一正方向的水平角．
(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③)．
(2)北偏西α，即由指北方向逆时针旋转α到达目标方向．
(3)南偏西等其他方向角类似．
（4）坡角与坡度
(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角)．
(2)坡度：坡面的铅直高度与水平长度之比(如图④，i为坡度)．坡度又称为坡比．
5.相关应用
（1）正弦定理的应用
= 1 \* GB3 \* MERGEFORMAT ①边化角，角化边
= 2 \* GB3 \* MERGEFORMAT ②大边对大角 大角对大边
= 3 \* GB3 \* MERGEFORMAT ③合分比：
（2）内角和定理：
= 1 \* GB3 \* MERGEFORMAT ①
同理有：，.
= 2 \* GB3 \* MERGEFORMAT ②；
= 3 \* GB3 \* MERGEFORMAT ③斜三角形中，
= 4 \* GB3 \* MERGEFORMAT ④；
= 5 \* GB3 \* MERGEFORMAT ⑤在中，内角成等差数列.
【题型精讲】
【题型一 已知边角元素解三角形】
必备技巧 已知边角元素解三角形技巧
正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素，基本思想是方程思想，即根据正弦定理、余弦定理列出关于未知元素的方程，通过解方程求得未知元素．
例1 （多选）(2023·山东济南一模）在中，角，，所对的边分别为，，，下列结论正确的是（ ）
A．B．
C．D．
例2（多选）(2023·重庆市育才中学高三二模）已知在中，角，，所对的边分别为，，，且，，，则下列说法正确的是
A．或B．
C．D．该三角形的面积为
例3(2023·安徽·合肥一六八中学模拟预测）在中，角A，B，C所对的边分别为a，b，c若，角C为钝角，.
(1)求的值；
(2)求边c的长.
【跟踪精练】
1．(2023·四川·树德中学模拟）在中，角所对的边分别为，若，则（ ）
A．B．或
C．D．或
2．(2023·河南·高三阶段练习）在中，内角，，所对的边分别是，，.若，，，则（ ）
A．B．C．或D．或
3.(2023·全国·高三专题练习）△ABC的内角A､B､C的对边分别为a､b､c，若a=4，b=3，c=2，则中线AD的长为（ ）
A．B．C．D．
【题型二 已知边角关系解三角形】
必备技巧 已知边角关系解三角形
正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化，解题时可以把已知条件化为角的三角函数关系，也可以把已知条件化为三角形边的关系．
例4 (2023·湖北·黄石市有色第一中学模拟预测）在中，内角的对边分别为，，，已知．
(1)若，求的值；
(2)若，的面积为，求边，的值．
例5 (2023·全国·高三专题练习）△的内角A，B，C的对边分别为a，b，c，已知△的面积为.
(1)证明：；
(2)若，求.
【跟踪精练】
1．（新课标Ⅰ）的内角，，的对边分别为，，．设．
（1）求；
（2）若，求．
2. (2023·山东潍坊·模拟预测）在中，内角的对边分别为，．
(1)求角；
(2)是边上的点，若，，求的值．
【题型三 判断三角形形状】
必备技巧 判断三角形形状的方法
（1）化边：通过因式分解、配方等得出边的相应关系．
（2）化角：通过三角恒等变换，得出内角的关系，此时要注意应用A＋B＋C＝π这个结论．
例6 (2023·全国·高三专题练习）在△ABC中，已知a2＋b2－c2＝ab，且2csAsinB＝sinC，则该三角形的形状是（ ）
A．直角三角形B．等腰三角形C．等边三角形D．钝角三角形
例7 (2023·四川省峨眉第二中学校月考）在中，已知，且，则的形状为（ ）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
【题型精练】
1. (2023·全国·高三专题练习）对于，有如下四个命题:
①若 ，则为等腰三角形，
②若，则是直角三角形
③若，则是钝角三角形
④若，则是等边三角形.
其中正确的命题序号是_________
2. (2023·全国·高三专题练习）在中，已知，则的形状一定是（ ）
A．等腰三角形B．直角三角形C．等边三角形D．等腰或直角三角形
【题型四 三角形解的个数问题】
例8 (2023·全国·高三专题练习）已知在中，、、分别为角、、的对边，则根据条件解三角形时恰有一解的一组条件是（ ）
A．，，B．，，
C．，，D．，，
例9 (2023·浙江·高三专题练习）中，角，，的对边分别是，，，，，若这个三角形有两解，则的取值范围是（ ）
A．B．
C．D．
【题型精练】
1. (2023·全国·高三专题练习）在中，根据下列条件解三角形，则其中有两个解的是（ ）
A．B．
C．D．
2. (2023·全国·高三专题练习）在中，角A，B，C的对边分别是a，b，c，若，满足条件，的三角形有两个，则的取值范围是 （ ）
A．B．C．D．
【题型五 解三角形中的最值范围问题】
方法技巧 解三角形中最值范围问题基本处理方法
1.用余弦定理结合基本不等式求解，
2.要求的量转化为某角的三角函数，求函数的最值或值域。（注意角的范围）
例10 (2023·宁夏石嘴山·一模）在中，角A，B，C的对边分别为a，b，c，D为的中点，若．
(1)求角B；
(2)若，求的最小值．
例11(2023·广东江门·模拟预测）在锐角中，内角A，B，C的对边分别是a，b，c，且满足.
(1)求角B的大小；
(2)若，求的取值范围.
【题型精练】
1. (2023·全国·高三课时练习）在锐角△ABC中，角A，B，C所对的边分别为a，b，c．已知2bsinA－eq \r(3)a＝0．
(1)求角B的大小；
(2)求csA＋csB＋csC的取值范围．
2. (2023·陕西高三期中）在∆ABC中，D在线段AB上，且AD=5，BD=3，CB=2CD.
（1）若cs∠CDB=−55，求∆ABC的面积； （2）求∆ABC的周长的最大值。
【题型六 解三角形实际应用问题】
方法技巧 解三角形实际应用
从实际问题中抽象出距离、高度、角度等数学问题，然后利用正弦定理、余弦定理求解，很好地体现了数学抽象的数学素养．
例12 (2023·山东省六地市部分学校高三3月线考）泉城广场上矗立着的“泉标”，成为泉城济南的标志和象征．为了测量“泉标”高度，某同学在“泉标”的正西方向的点A处测得“泉标”顶端的仰角为，沿点A向北偏东前进100 m到达点B，在点B处测得“泉标”顶端的仰角为，则“泉标”的高度为（ ）
A．50 mB．100 mC．120 mD．150 m
【题型精练】
1. (2023·山东泰安·高三期末）在某海域处的巡逻船发现南偏东方向，相距海里的处有一可疑船只，此可疑船只正沿射线（以点为坐标原点，正东，正北方向分别为轴，轴正方向，1海里为单位长度，建立平面直角坐标系）方向匀速航行.巡逻船立即开始沿直线匀速追击拦截，巡逻船出发小时后，可疑船只所在位置的横坐标为.若巡逻船以30海里/小时的速度向正东方向追击，则恰好1小时与可疑船只相遇.
(1)求的值；
(2)若巡逻船以海里/小时的速度进行追击拦截，能否搃截成功？若能，求出搃截时间，若不能，请说明理由.
定理
正弦定理
余弦定理
内容
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)＝2R
a2＝b2＋c2－2bccs A；
b2＝c2＋a2－2cacs B；
c2＝a2＋b2－2abcs C
变形
(1)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；
(2)sin A＝eq \f(a,2R)，sin B＝eq \f(b,2R)，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝sin A∶sin B∶sin C；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
cs A＝eq \f(b2＋c2－a2,2bc)；
cs B＝eq \f(c2＋a2－b2,2ac)；
cs C＝eq \f(a2＋b2－c2,2ab)
A为锐角
A为钝角或直角
图形
关系式
解的个数
一解
两解
一解
一解
无解
4.5 解三角形6大常考题型
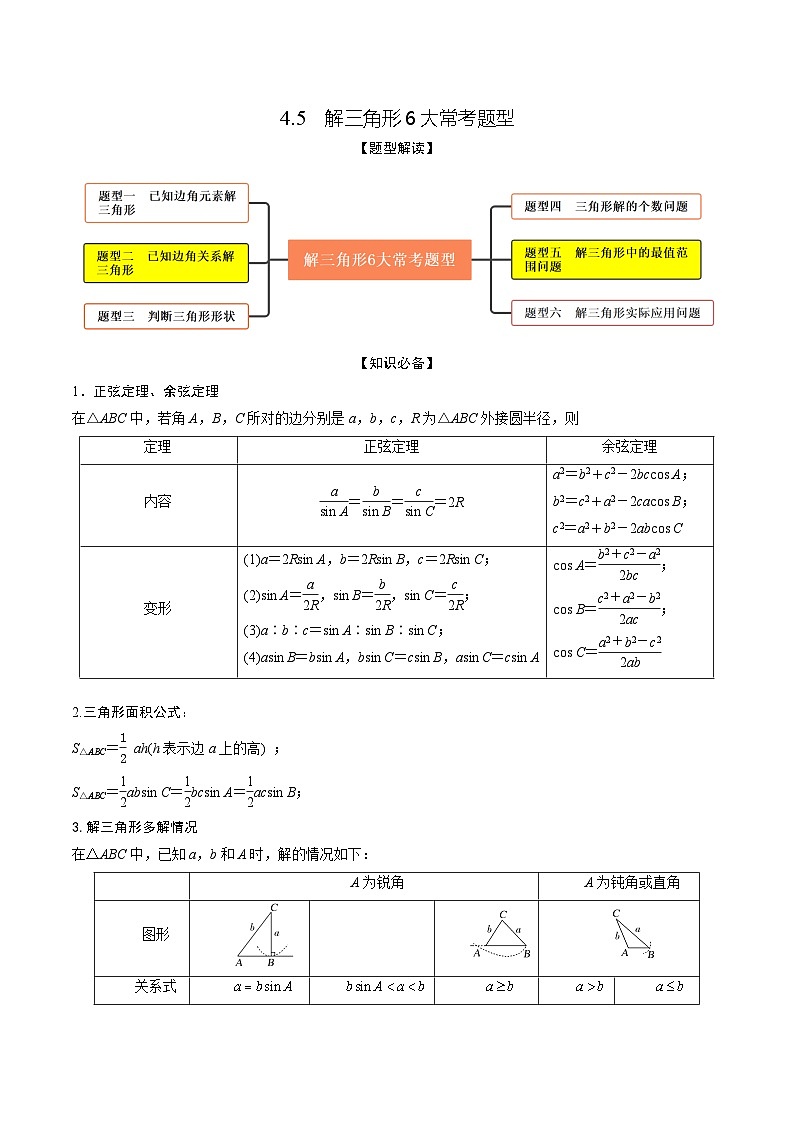
【题型解读】
【知识必备】
1．正弦定理、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.三角形面积公式：
S△ABC＝eq \f(1,2) ah(h表示边a上的高) ；
S△ABC＝eq \f(1,2)absin C＝eq \f(1,2)bcsin A＝eq \f(1,2)acsin B；
3.解三角形多解情况
在△ABC中，已知a，b和A时，解的情况如下：
4.实际应用
（1）仰角和俯角
在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．
（2）方位角
从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．
（3）方向角：相对于某一正方向的水平角．
(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③)．
(2)北偏西α，即由指北方向逆时针旋转α到达目标方向．
(3)南偏西等其他方向角类似．
（4）坡角与坡度
(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角)．
(2)坡度：坡面的铅直高度与水平长度之比(如图④，i为坡度)．坡度又称为坡比．
5.相关应用
（1）正弦定理的应用
= 1 \* GB3 \* MERGEFORMAT ①边化角，角化边
= 2 \* GB3 \* MERGEFORMAT ②大边对大角 大角对大边
= 3 \* GB3 \* MERGEFORMAT ③合分比：
（2）内角和定理：
= 1 \* GB3 \* MERGEFORMAT ①
同理有：，.
= 2 \* GB3 \* MERGEFORMAT ②；
= 3 \* GB3 \* MERGEFORMAT ③斜三角形中，
= 4 \* GB3 \* MERGEFORMAT ④；
= 5 \* GB3 \* MERGEFORMAT ⑤在中，内角成等差数列.
【题型精讲】
【题型一 已知边角元素解三角形】
必备技巧 已知边角元素解三角形技巧
正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素，基本思想是方程思想，即根据正弦定理、余弦定理列出关于未知元素的方程，通过解方程求得未知元素．
例1 （多选）(2023·山东济南一模）在中，角，，所对的边分别为，，，下列结论正确的是（ ）
A．B．
C．D．
答案：ABC
【解析】由在中，角，，所对的边分别为，，，知：
在选项中，由余弦定理得：，故正确；
在选项中，由正弦定理得：，
，故正确；
在选项中，，
由余弦定理得：，
整理，得，故正确；
在选项中，由余弦定理得：，
故错误.
故选：.
例2（多选）(2023·重庆市育才中学高三二模）已知在中，角，，所对的边分别为，，，且，，，则下列说法正确的是
A．或B．
C．D．该三角形的面积为
答案：BC
【解析】由余弦定理得，所以.
由正弦定理得，所以，
由于，所以.所以.
三角形的面积为.
故BC选项正确，AD选项错误.故选：BC
例3(2023·安徽·合肥一六八中学模拟预测）在中，角A，B，C所对的边分别为a，b，c若，角C为钝角，.
(1)求的值；
(2)求边c的长.
答案：(1) (2)
【解析】(1)因为C为钝角，由，则，
则， C为钝角可得为锐角，
所以，，
可得.
(2)由（1）可知：，则，，
则，
正弦定理：，，
可得：.
【跟踪精练】
1．(2023·四川·树德中学模拟）在中，角所对的边分别为，若，则（ ）
A．B．或
C．D．或
答案：C
【解析】由得，，由余弦定理得，
因为，所以.故选：C
2．(2023·河南·高三阶段练习）在中，内角，，所对的边分别是，，.若，，，则（ ）
A．B．C．或D．或
答案：A
【解析】由正弦定理可得，则，
故或.因为，所以，所以.故选：A
3.(2023·全国·高三专题练习）△ABC的内角A､B､C的对边分别为a､b､c，若a=4，b=3，c=2，则中线AD的长为（ ）
A．B．C．D．
答案：D
【解析】如图，由余弦定理得AB2=DA2+DB2－2DA·DBcs∠ADB，
AC2=DA2+DC2－2DA·DCcs∠ADC，又cs∠ADB=－cs∠ADC
两式相加得AB2+AC2=2DA2+DB2+DC2，即22+32=2DA2+22+22，∴2DA2=5，∴DA=.故选：D
【题型二 已知边角关系解三角形】
必备技巧 已知边角关系解三角形
正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化，解题时可以把已知条件化为角的三角函数关系，也可以把已知条件化为三角形边的关系．
例4 (2023·湖北·黄石市有色第一中学模拟预测）在中，内角的对边分别为，，，已知．
(1)若，求的值；
(2)若，的面积为，求边，的值．
答案：(1) (2)，或，
【解析】(1)因为，
由正弦定理得，
即，
因为，所以，
由为三角形内角得；
由，则，
所以，
，
；
(2)因为的面积，所以，
由余弦定理 得,则，
由解得，或，.
例5 (2023·全国·高三专题练习）△的内角A，B，C的对边分别为a，b，c，已知△的面积为.
(1)证明：；
(2)若，求.
答案：(1)证明见解析； (2).
【解析】(1)由题设，，又，
所以，由正弦定理可得，
所以，又，
所以，即.
(2)由（1）及题设，，且，
所以，则，故，
又，可得，
若，则，而，故不合题设；
所以，
所以.
【跟踪精练】
1．（新课标Ⅰ）的内角，，的对边分别为，，．设．
（1）求；
（2）若，求．
【解析】（1）的内角，，的对边分别为，，．
设．
则，
由正弦定理得：，，，．
（2），，由正弦定理得，
解得，，，
．
2. (2023·山东潍坊·模拟预测）在中，内角的对边分别为，．
(1)求角；
(2)是边上的点，若，，求的值．
答案：(1) (2)
【解析】(1)由得：，
由正弦定理得：，
，又，，
；
有意义，，，即，
又，.
(2)
，，设，则，
在中，由正弦定理得：，即；
在中，由余弦定理得：；
，解得：，
即，又，.
【题型三 判断三角形形状】
必备技巧 判断三角形形状的方法
（1）化边：通过因式分解、配方等得出边的相应关系．
（2）化角：通过三角恒等变换，得出内角的关系，此时要注意应用A＋B＋C＝π这个结论．
例6 (2023·全国·高三专题练习）在△ABC中，已知a2＋b2－c2＝ab，且2csAsinB＝sinC，则该三角形的形状是（ ）
A．直角三角形B．等腰三角形C．等边三角形D．钝角三角形
答案：C
【解析】∵a2＋b2－c2＝ab，∴，又，∴，
由2csAsinB＝sinC，得∴，即，又，
故三角形为等边三角形.故选：C
例7 (2023·四川省峨眉第二中学校月考）在中，已知，且，则的形状为（ ）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
答案：B
【解析】由题意,,
则,
又，则,
由可得，即，
所以，由，知，
综上可知即的形状是等边三角形.
故选：B
【题型精练】
1. (2023·全国·高三专题练习）对于，有如下四个命题:
①若 ，则为等腰三角形，
②若，则是直角三角形
③若，则是钝角三角形
④若，则是等边三角形.
其中正确的命题序号是_________
答案：③④
【解析】对于①可推出或，故不正确；
②若，显然满足条件，但不是直角三角形；
③由正弦定理得，所以，是钝角三角形；
④由正弦定理知，由于半角都是锐角，所以，三角形是等边三角形.
故答案为：③④
2. (2023·全国·高三专题练习）在中，已知，则的形状一定是（ ）
A．等腰三角形B．直角三角形C．等边三角形D．等腰或直角三角形
答案：B
【解析】由正弦定理得，整理得：
即，又因为,所以,
所以，移项得：,所以三角形一定为直角三角形.故选：B
【题型四 三角形解的个数问题】
例8 (2023·全国·高三专题练习）已知在中，、、分别为角、、的对边，则根据条件解三角形时恰有一解的一组条件是（ ）
A．，，B．，，
C．，，D．，，
答案：B
【解析】对于A选项，由正弦定理可得，且，故有两解；
对于B选项，由正弦定理可得，且，故只有一解；
对于C选项，由正弦定理可得，故无解；
对于D选项，因为，则角为的最大内角，且，故无解.故选：B.
例9 (2023·浙江·高三专题练习）中，角，，的对边分别是，，，，，若这个三角形有两解，则的取值范围是（ ）
A．B．
C．D．
答案：B
【解析】因为这个三角形有两解，故满足，即，解得.故选：B
【题型精练】
1. (2023·全国·高三专题练习）在中，根据下列条件解三角形，则其中有两个解的是（ ）
A．B．
C．D．
答案：D
【解析】对于A选项，，，，又，
由正弦定理得：，，
三角形三边确定，此时三角形只有一解，不合题意；
对于B选项，，，，
由余弦定理得：，
三角形三边唯一确定，此时三角形有一解，不合题意；
对于C选项，，三边均为定值，三角形唯一确定，故选项C不合题意；
对于D选项，，，，由正弦定理得：，
，，，有两解，符合题意，故选：D.
2. (2023·全国·高三专题练习）在中，角A，B，C的对边分别是a，b，c，若，满足条件，的三角形有两个，则的取值范围是 （ ）
A．B．C．D．
答案：C
【解析】因为，，由正弦定理可得，所以，
又满足题意的三角形有两个，所以只需，即，
解得.故选：C.
【题型五 解三角形中的最值范围问题】
方法技巧 解三角形中最值范围问题基本处理方法
1.用余弦定理结合基本不等式求解，
2.要求的量转化为某角的三角函数，求函数的最值或值域。（注意角的范围）
例10 (2023·宁夏石嘴山·一模）在中，角A，B，C的对边分别为a，b，c，D为的中点，若．
(1)求角B；
(2)若，求的最小值．
答案：(1)(2)
【解析】(1)解：由，
利用正弦定理可得：，，
∵，∴，∴；
(2)由D为的中点，∴，
∴，，
又∵，∴ ， ∴，∴，
当且仅当时，取最小值．
例11(2023·广东江门·模拟预测）在锐角中，内角A，B，C的对边分别是a，b，c，且满足.
(1)求角B的大小；
(2)若，求的取值范围.
答案：(1)(2)
【解析】(1)因为，
所以由正弦定理可得，化简得，
所以由余弦定理得，
因为，所以
(2)因为，所以,由正弦定理得，，
所以，
因为为锐角三角形，所以，得，所以，
所以，所以，，所以，即的取值范围为
【题型精练】
1. (2023·全国·高三课时练习）在锐角△ABC中，角A，B，C所对的边分别为a，b，c．已知2bsinA－eq \r(3)a＝0．
(1)求角B的大小；
(2)求csA＋csB＋csC的取值范围．
【解析】(1)由正弦定理，得2sinBsinA＝eq \r(3)sinA，又在△ABC中，sin A>0，
故sin B＝eq \f(\r(3),2)，由题意得B＝eq \f(π,3)．
(2)由A＋B＋C＝π，得C＝eq \f(2π,3)－A．由△ABC是锐角三角形，得A∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,2))) ．
由csC＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3)－A))＝－eq \f(1,2)csA＋eq \f(\r(3),2)sinA，得
csA＋csB＋csC＝eq \f(\r(3),2)sin A＋eq \f(1,2)cs A＋eq \f(1,2)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(A＋\f(π,6)))＋eq \f(1,2)∈eq \b\lc\(\rc\](\a\vs4\al\c1(\f(\r(3)＋1,2)，\f(3,2)))．
故csA＋csB＋csC的取值范围是eq \b\lc\(\rc\](\a\vs4\al\c1(\f(\r(3)＋1,2)，\f(3,2)))．
2. (2023·陕西高三期中）在∆ABC中，D在线段AB上，且AD=5，BD=3，CB=2CD.
（1）若cs∠CDB=−55，求∆ABC的面积； （2）求∆ABC的周长的最大值。
答案：（1）8 （2）8+45
【解析】（1）设CD=m，则CB=2m，
在∆BCD中，由余弦定理知，cs∠CDB=CD2+BD2−BC22CD∙BD=3−m22m=−55，
解得m=5，∴CD=5，CB=25，
由余弦定理知，cs∠CBD=BC2+BD2−CD22BC∙BD=9+20−52×3×25=255，
∴sin∠CBD=1−cs2∠CBD=55，
故∆ABC的面积为S=12BC∙ABsin∠CBD=12×25×8×55=8.
（2）由（1）知，CB=m，CB=2m，cs∠CDB=3−m22m，∵∠CDA+∠CDB=π，
∴cs∠CDA=−cs∠CDB=3−m22m，在∆ACD中，由余弦定理知，
AC2=AD2+CD2−2AD∙CDcs∠ADC
=25+m2−2×5×m2−32m=4(10−m2).
∴AC=210−m2，
设∆ABC的周长为z，
则z=AB+BC+AC=8+2m+10−m2≥8+2m2+10−m222=8+45，
当且仅当m=10−m2，即m=5时，等号成立，
故∆ABC的周长的最大值为8+45.
【题型六 解三角形实际应用问题】
方法技巧 解三角形实际应用
从实际问题中抽象出距离、高度、角度等数学问题，然后利用正弦定理、余弦定理求解，很好地体现了数学抽象的数学素养．
例12 (2023·山东省六地市部分学校高三3月线考）泉城广场上矗立着的“泉标”，成为泉城济南的标志和象征．为了测量“泉标”高度，某同学在“泉标”的正西方向的点A处测得“泉标”顶端的仰角为，沿点A向北偏东前进100 m到达点B，在点B处测得“泉标”顶端的仰角为，则“泉标”的高度为（ ）
A．50 mB．100 mC．120 mD．150 m
答案：A
【解析】如图,为“泉标”高度,设高为米，由题意,平面,米,，
．
在中,,在中,,
在中,，,，,
由余弦定理可得，
解得或 (舍去),故选：B.
【题型精练】
1. (2023·山东泰安·高三期末）在某海域处的巡逻船发现南偏东方向，相距海里的处有一可疑船只，此可疑船只正沿射线（以点为坐标原点，正东，正北方向分别为轴，轴正方向，1海里为单位长度，建立平面直角坐标系）方向匀速航行.巡逻船立即开始沿直线匀速追击拦截，巡逻船出发小时后，可疑船只所在位置的横坐标为.若巡逻船以30海里/小时的速度向正东方向追击，则恰好1小时与可疑船只相遇.
(1)求的值；
(2)若巡逻船以海里/小时的速度进行追击拦截，能否搃截成功？若能，求出搃截时间，若不能，请说明理由.
答案：(1)
(2)能够拦截成功拦截，时间为2小时
【解析】(1)解：由题意，直线的倾斜角为，
若巡逻船以30海里/小时的速度向正东方向追击，设1小时后两船相遇于点C，
如图所示，则轴，，且关于y轴对称，
所以，所以.
(2)解：若巡逻船以海里/小时进行追击，设t小时后两船相遇于点D，如图所示，
则，，，，
因为
可得
整理得，解得或（舍去），
所以能够拦截成功拦截时间为2小时.
定理
正弦定理
余弦定理
内容
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)＝2R
a2＝b2＋c2－2bccs A；
b2＝c2＋a2－2cacs B；
c2＝a2＋b2－2abcs C
变形
(1)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；
(2)sin A＝eq \f(a,2R)，sin B＝eq \f(b,2R)，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝sin A∶sin B∶sin C；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
cs A＝eq \f(b2＋c2－a2,2bc)；
cs B＝eq \f(c2＋a2－b2,2ac)；
cs C＝eq \f(a2＋b2－c2,2ab)
A为锐角
A为钝角或直角
图形
关系式
解的个数
一解
两解
一解
一解
无解