高考数学大一轮复习精讲精练(新高考地区)7.5空间几何体中平行的判定和性质(精练)(原卷版+解析)

这是一份高考数学大一轮复习精讲精练(新高考地区)7.5空间几何体中平行的判定和性质(精练)(原卷版+解析)，共21页。


【题型一 线面平行的判定】
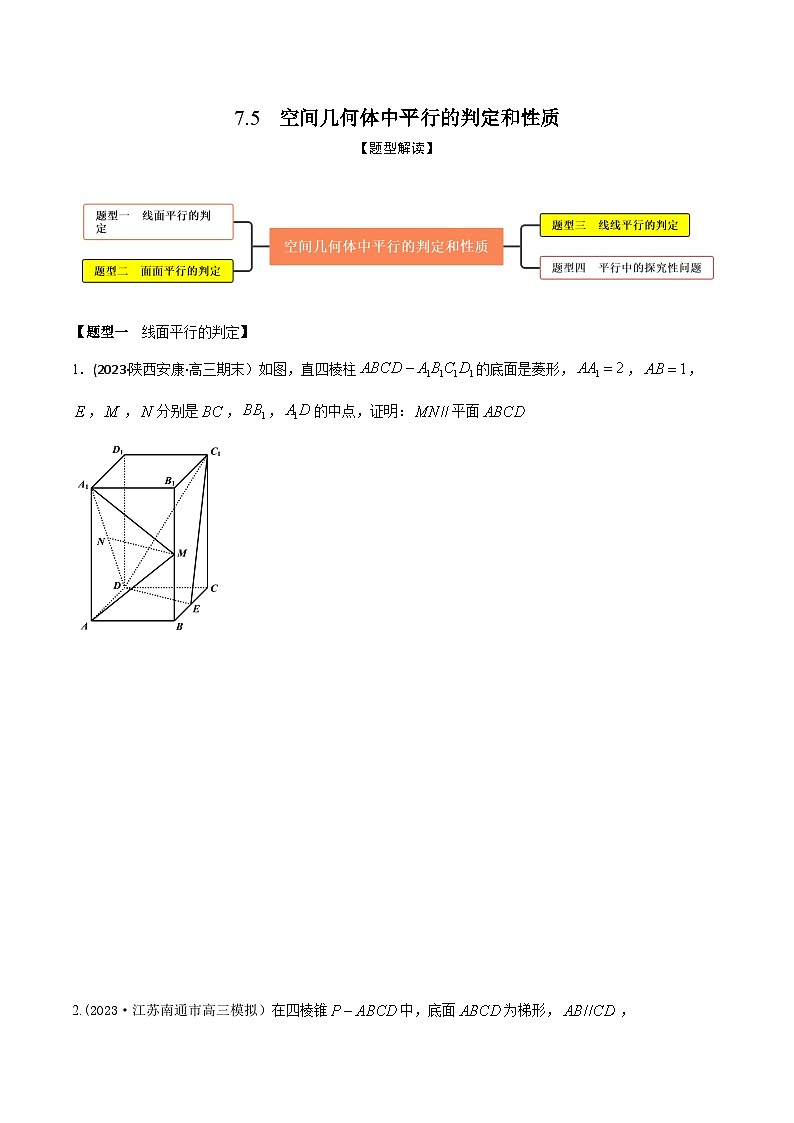
1．(2023·陕西安康·高三期末）如图，直四棱柱的底面是菱形，，，，，分别是，，的中点，证明：平面
2.(2023·江苏南通市高三模拟）在四棱锥中，底面为梯形，，，若为的中点，求证：平面
3. (2023·陕西高三模拟）如图所示，在四棱锥中，平面，E是的中点.
(1)求证：//平面
(2)求证：//平面.
4. (2023·海原县高三模拟）如图，在四棱锥中，底面为直角梯形，其中，，，且．点在棱上，点为中点，证明：若，则直线平面
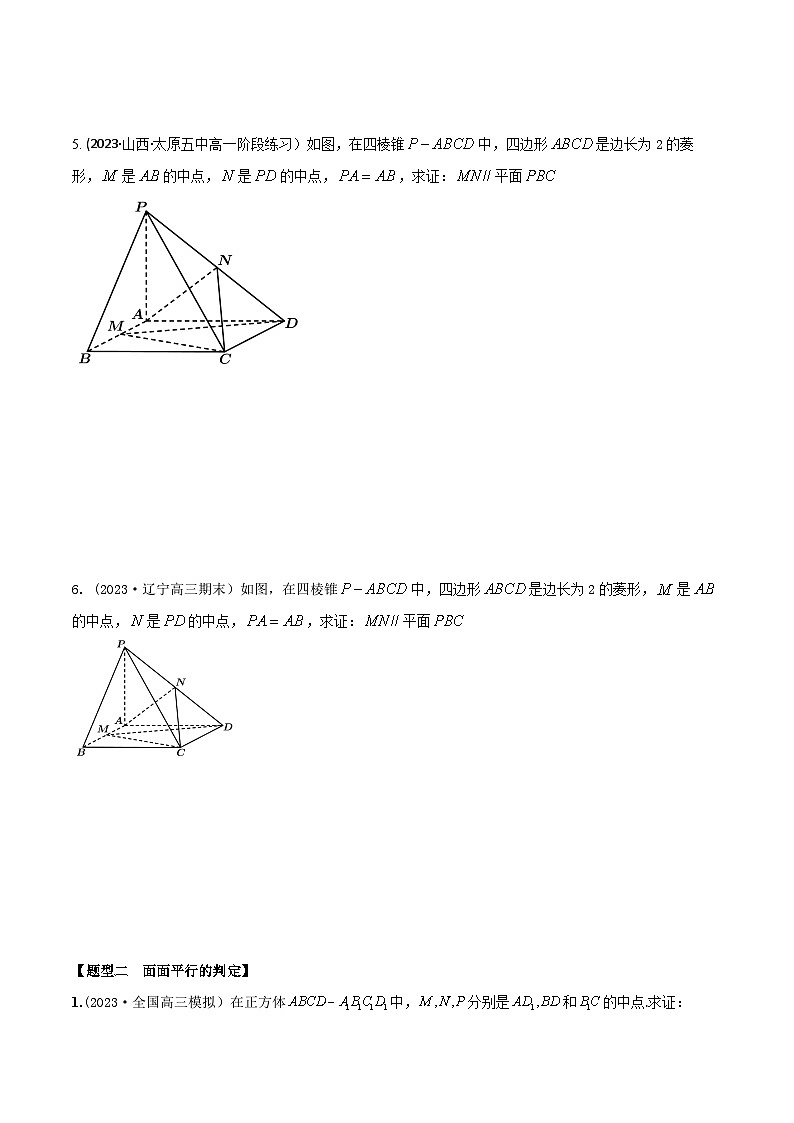
5. (2023·山西·太原五中高一阶段练习）如图，在四棱锥中，四边形是边长为2的菱形，是的中点，是的中点，，求证：平面
6. (2023·辽宁高三期末）如图，在四棱锥中，四边形是边长为2的菱形，是的中点，是的中点，，求证：平面
【题型二 面面平行的判定】
1.(2023·全国高三模拟）在正方体中，分别是和的中点.求证：
(1)平面.
(2)平面平面.
2.(2023·河北衡水中学高三模拟）如图，四边形ABCD是边长为的菱形，BB1＝DD1＝2，E，F分别是AD1，AB1的中点，证明：平面BDEF∥平面CB1D1
3. (2023·安徽·合肥市第六中学高一期中）如图，四棱台中，底面为直角梯形，，，底面，，为棱的中点，证明：平面
4. (2023·全国高三模拟）如图，在四棱锥中，，，，，、、分别为线段、、的中点，证明：平面平面.
【题型三 线线平行的判定】
1.(2023·江西高三模拟）如图（1），在梯形中，且，线段上有一点E，满足，，现将分别沿折起，使，得到如图（2）所示的几何体．求证：
2.(2023·重庆八中高三阶段练习）如图所示，四棱锥的底面是直角梯形，，底面，过的平面交于，交于（与不重合）.求证：；
3．(2023·全国·高三专题练习）如图，在四面体中，，分别为，的中点，过的平面与，分别交于点，.求证：
4. (2023·全国·高三专题练习）如图，平面，平面，，求证：
【题型四 平行中的探究性问题】
1.(2023·山东·模拟预测）如图，已知平面，平面，，设是直线上的点，当点在何位置时，直线平面？请说明理由
2.(2023·福建·三明一中模拟预测）已知四棱柱的底面是边长为2的菱形，且，平面，，于点，试问在线段上是否存在一点，使得平面？若存在，求出点的位置；若不存在，请说明理由；
3. (2023·广东佛山市高三模拟）在三棱锥中，平面，，，，为的中点，为的中点，在线段上是否存在一点，使平面？若存在，指出点的位置并给出证明，若不存在，说明理由
7.5 空间几何体中平行的判定和性质
【题型解读】

【题型一 线面平行的判定】
1．(2023·陕西安康·高三期末）如图，直四棱柱的底面是菱形，，，，，分别是，，的中点，证明：平面
答案：证明见解析
【解析】连接，
分别为中点，；
由直四棱柱特点知：，，又为中点，，
四边形为平行四边形，，
又平面，平面，平面；
2.(2023·江苏南通市高三模拟）在四棱锥中，底面为梯形，，，若为的中点，求证：平面
答案：证明见解析
【解析】证明：∵在梯形中，，，为的中点，
所以且，∴四边形为平行四边形，所以，
∵平面，平面，所以平面．
3. (2023·陕西高三模拟）如图所示，在四棱锥中，平面，E是的中点.
(1)求证：//平面
(2)求证：//平面.
答案：(1)证明见解析；(2)证明见解析
【解析】(1)因为平面，平面，平面平面，所以，
又平面，平面，则平面；
(2)
取中点，连接，易得，且，由（1）知且，
则且，则四边形为平行四边形，则，又平面，平面，则平面.
4. (2023·海原县高三模拟）如图，在四棱锥中，底面为直角梯形，其中，，，且．点在棱上，点为中点，证明：若，则直线平面
答案：证明见解析
【解析】在上取一点，使得，连接，
，，又平面，平面，
平面；
，，，
，，四边形为平行四边形，，
又平面，平面，平面；
，平面，平面平面，
平面，平面.
5. (2023·山西·太原五中高一阶段练习）如图，在四棱锥中，四边形是边长为2的菱形，是的中点，是的中点，，求证：平面
答案：证明见解析
【解析】证明：如图①，取的中点，连接，，
因为是的中点，所以且.
因为四边形是菱形，是的中点，所以且，
从而且，
所以四边形是平行四边形，从而.
又平面，平面，所以平面.
6. (2023·辽宁高三期末）如图，在四棱锥中，四边形是边长为2的菱形，是的中点，是的中点，，求证：平面
答案：证明见解析
【解析】证明：如图①，取的中点，连接，，
因为是的中点，所以且.
因为四边形是菱形，是的中点，所以且，
从而且，
所以四边形是平行四边形，从而.
又平面，平面，所以平面.
【题型二 面面平行的判定】
1.(2023·全国高三模拟）在正方体中，分别是和的中点.求证：
(1)平面.
(2)平面平面.
答案：(1)证明见解析(2)证明见解析
【解析】（1）连接，因为四边形为正方形，为中点，所以为中点，又因为为中点，所以.因为平面平面，所以平面，
连接，因为四边形为正方形，为中点，所以为中点.又因为为中点，所以.因为平面平面所以平面.由（1）知平面，又，平面，所以平面平面.
2.(2023·河北衡水中学高三模拟）如图，四边形ABCD是边长为的菱形，BB1＝DD1＝2，E，F分别是AD1，AB1的中点，证明：平面BDEF∥平面CB1D1
答案：证明见解析
【解析】证明：连接，交于点，连接，则为的中点，
∵是的中点，
平面,平面,所以平面
又是的中点
平面,平面,所以平面
又平面,, 所以平面平面．
3. (2023·安徽·合肥市第六中学高一期中）如图，四棱台中，底面为直角梯形，，，底面，，为棱的中点，证明：平面
答案：证明见解析
【解析】在上取点，使，连接交于点，连接，
设，交于点，由，则，，
∴，即，又面，面，
∴面，同理可得/面，又，
∴面面，又面，
∴平面；
4. (2023·全国高三模拟）如图，在四棱锥中，，，，，、、分别为线段、、的中点，证明：平面平面.
答案：证明见解析
【解析】如图，连接、，与相交于点，连接，
因为，，为线段的中点，，
所以四边形为矩形，为的中点，
因为为的中点，所以为的中位线，，
因为平面，平面，所以平面，
因为、分别为线段、的中点，所以，
因为平面，平面，所以平面，
因为平面，平面，，
所以平面平面
【题型三 线线平行的判定】
1.(2023·江西高三模拟）如图（1），在梯形中，且，线段上有一点E，满足，，现将分别沿折起，使，得到如图（2）所示的几何体．求证：
答案：证明见解析；
【解析】图（1）中，，则，而，即，
在中，，有，
同理可得，则，
图（2）中，，则，而，平面，则有平面，
在中，，则，又，，平面，因此平面，
所以.
2.(2023·重庆八中高三阶段练习）如图所示，四棱锥的底面是直角梯形，，底面，过的平面交于，交于（与不重合）.求证：；
答案：证明见解析
【解析】证明：在梯形中，，平面，平面，
平面.
又平面，平面平面，
所以.
3．(2023·全国·高三专题练习）如图，在四面体中，，分别为，的中点，过的平面与，分别交于点，.求证：
答案：（1）证明见解析；（2）.
【解析】因为，分别为，的中点，所以，
因为平面，平面
所以平面
又平面平面，平面
所以，所以.
4. (2023·全国·高三专题练习）如图，平面，平面，，求证：
答案：证明见解析
【解析】依题意，平面，平面，∴平面，
又平面，，∴平面平面，
∴平面平面，平面平面，∴；
【题型四 平行中的探究性问题】
1.(2023·山东·模拟预测）如图，已知平面，平面，，设是直线上的点，当点在何位置时，直线平面？请说明理由
答案：点是的中点，理由见解析
【解析】当点是的中点时，平面.
理由如下：如下图，取的中点，连接、、，则且，
因为平面，平面，所以.
又，所以且，
所以四边形是平行四边形，所以.
因为平面，平面，所以平面；
2.(2023·福建·三明一中模拟预测）已知四棱柱的底面是边长为2的菱形，且，平面，，于点，试问在线段上是否存在一点，使得平面？若存在，求出点的位置；若不存在，请说明理由；
答案：存在，为线段的中点；理由见解析
【解析】当为线段的中点时，平面.
下面给出证明：
取的中点，连接，，则，且，
所以四边形为平行四边形，所以.
因为，，所以为的中点，
又为的中点，，，所以，且，
所以四边形为平行四边形，所以，且，又，，
所以，且，所以四边形为平行四边形，
所以，所以，
又平面，平面，所以平面，
3. (2023·广东佛山市高三模拟）在三棱锥中，平面，，，，为的中点，为的中点，在线段上是否存在一点，使平面？若存在，指出点的位置并给出证明，若不存在，说明理由
答案：存在；点为上的靠近的四等分点；证明见解析
【解析】存在点为上的靠近的四等分点即，平面，
证明如下：取的中点，连接，，
则，
因为平面，平面，所以平面，
因为，，
所以，又平面，平面，
所以平面，
又，平面，
所以平面平面，
又平面，所以平面．