人教版数学八年级上册 11 章末复习 PPT课件

这是一份人教版数学八年级上册 11 章末复习 PPT课件，共22页。
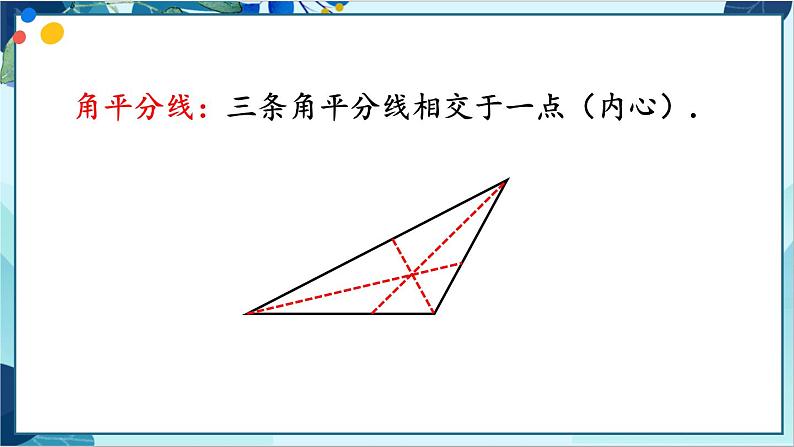
章 末 复 习人教版·八年级上册1. 三角形的三边关系：三角形的两边之和大于第三边，两边之差小于第三边.2. 三角形的分类按边分三边都不相等的三角形等腰三角形腰和底不等的等腰三角形等边三角形按角分锐角三角形直角三角形钝角三角形3. 三角形的高、中线与角平分线高：顶点与对边垂足间的线段，三条高或其延长线相交于一点（垂心）.中线：顶点与对边中点间的线段，三条中线相交于一点（重心）.角平分线：三条角平分线相交于一点（内心）.4. 三角形的内角和与外角和（1）三角形的内角和等于 180°；（2）三角形的一个外角等于与它不相邻的两个内角的和；（3）三角形的一个外角大于和它不相邻的任何一个内角；（4）三角形的外角和等于 360°.直角三角形性质判定直角三角形的两个锐角_____有两个角_____的三角形是直角三角形互余互余5. 多边形及其内角和在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形.正多边形的各个角都相等，各条边都相等.n 边形内角和等于(n-2)×180 °(n ≥3的整数）n 边形的外角和等于360°正多边形的每个内角的度数是正多边形的每个外角的度数是n 边形对角线的条数为考点一 三角形的三边关系1. 已知两条线段的长分别是 3 cm、8 cm ，要想拼成一个三角形， 且第三条线段 a 的长为奇数，问第三条线段应取多长？解：由三角形两边之和大于第三边,两边之差小于第三边得8-3 < a < 8+3∴ 5 < a < 11∵第三边长为奇数∴第三条边长为 7 cm 或 9 cm.2. 等腰三角形的周长为 16，其一边长为 6，求另两边长.解：由于题中没有指明边长为 6 的边是底还是腰，∴分两种情况讨论：①当 6 为底边长时，腰长为 (16-6)÷2 = 5，这时另两边长分别为 5，5；②当 6 为腰长时，底边长为 16-6-6 = 4，这时另两边长分别为 6，4.综上所述，另两边长为 5，5 或 6，4.考点二 三角形中的重要线段3. 如图，CD 为△ABC 的 AB 边上的中线，△BCD 的周长 比 △ACD 的周长大 3 cm，BC = 8 cm，求边 AC 的长．解：∵CD 为△ABC 的 AB 边上的中线∴AD = BD∵△BCD 的周长比△ACD 的周长大 3 cm∴(BC + BD + CD)-(AC + AD + CD) = 3cm∴BC-AC = 3cm∵BC = 8cm∴AC = 5cm4. 如图，D 是△ABC 的边 BC 上任意一点，E、F 分别是线段 AD、CE 的中点，且△ABC 的面积为 24，求△BEF 的面积．解：∵点 E 是 AD 的中点∵点 F 是 CE 的中点考点三 有关三角形内、外角的计算5. ∠A，∠B，∠C 是 △ABC 的三个内角，且分别满足下列条件， 求∠A，∠B，∠C 中未知角的度数. （1）∠A－∠B ＝ 16°，∠C＝ 54°； （2）∠A : ∠B : ∠C ＝ 2 : 3 : 4.解:（1）由∠C ＝ 54°知∠A＋∠B ＝ 180°－54°＝ 126°①∠A－∠B ＝ 16°②由①②解得∠A＝ 71°，∠B ＝ 55°;考点三 有关三角形内、外角的计算5. ∠A，∠B，∠C 是 △ABC 的三个内角，且分别满足下列条件， 求∠A，∠B，∠C 中未知角的度数. （1）∠A－∠B ＝ 16°，∠C＝ 54°； （2）∠A : ∠B : ∠C ＝ 2 : 3 : 4.（2）设∠A＝ 2x，∠B＝ 3x，∠C = 4x .则 2x + 3x + 4x = 180° 解得 x = 20°∴∠A＝ 40°，∠B＝ 60°，∠C＝ 80°.6. 如图，在△ABC 中，D 是 BC 边上一点，∠1 = ∠2，∠3 = ∠4， ∠BAC = 63°，求∠DAC 的度数．解：设∠1 = ∠2 = x，则∠4 = ∠3 = 2x．∵∠BAC = 63°∴∠2 + ∠4 = 117°即 x + 2x = 117°∴ x = 39°∴∠3 = ∠4 = 78°∴∠DAC = 180°-∠3-∠4 = 24°ABCD1234考点四 多边形的内角和与外角和7. 已知一个多边形的每个外角都是其相邻内角度数的 ， 求这个多边形的边数.解：设此多边形的外角的度数为 x，则内角的度数为 4x.则 x + 4x = 180°解得 x = 36°∴边数 n = 360°÷ 36°= 108. 如图，五边形 ABCDE 的内角都相等，且∠1 = ∠2，∠3 = ∠4． 求∠CAD 的度数．解：∵五边形的内角和是 540°∴每个内角为 540°÷5 = 108°∴∠E = ∠B = ∠BAE = 108°又∵∠1 = ∠2，∠3 = ∠4由三角形内角和定理可知∠1 = ∠2 = ∠3 = ∠4 =（180°-108°）÷2 = 36°∴∠CAD = ∠BAE-∠1-∠3 = 108°-36°-36°= 36°通过这节课的学习，你有什么收获？1.从教材习题中选取；2.完成练习册本课时的习题.