人教版数学八年级上册 12.4 章末复习 PPT课件

这是一份人教版数学八年级上册 12.4 章末复习 PPT课件，共24页。
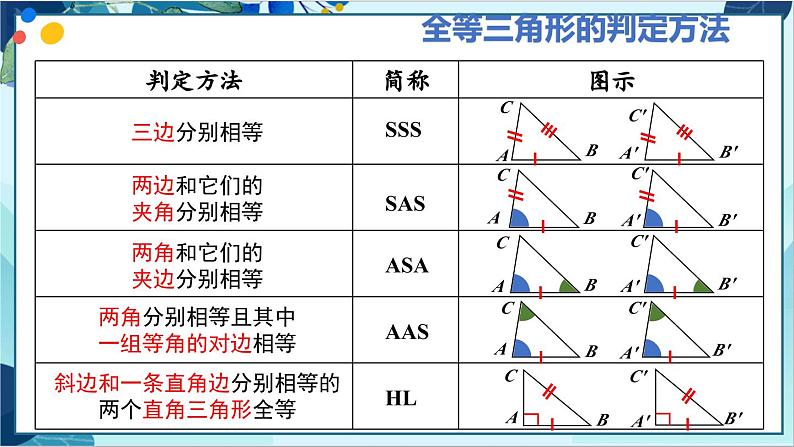
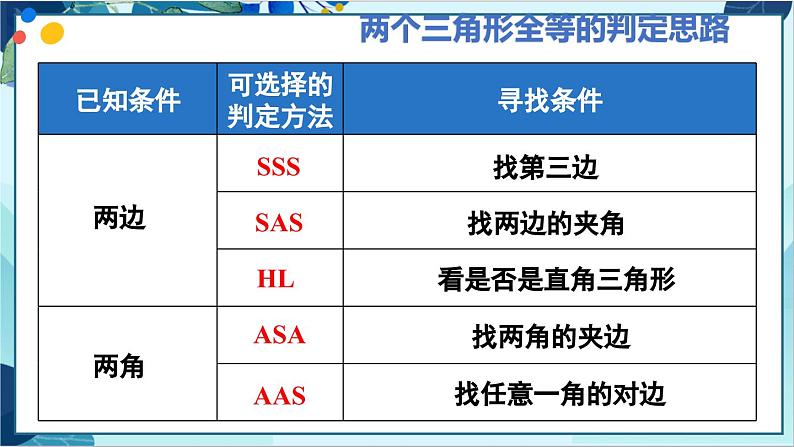
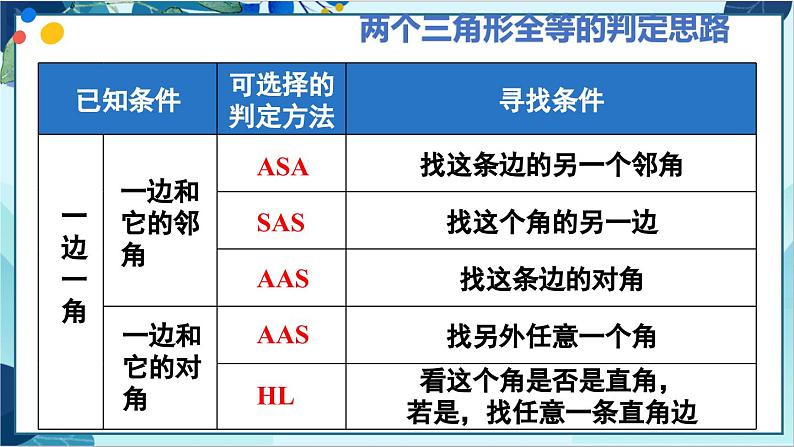
R·数学八年级上册章末复习数学复习学习目标1.掌握全等三角形的性质和判定定理2.理解角平分线的性质和判定以及与全等三角形的联系3.灵活运用全等三角形的性质和判定解决几何问题本章知识结构图边边边，边角边，角边角，角角边，斜边、直角边判定全等三角形全等形应用性质对应边相等，对应角相等知识框架全等三角形全等形全等三角形角平分线能够完全重合的两个图形定义：能够完全重合的两个三角形性质：对应边相等，对应角相等判定：SSS、SAS、ASA、AAS、HL性质：判定：角平分线上的点到角的两边的距离相等角的内部到角两边的距离相等的点在角的平分线上重点梳理全等三角形的性质全等三角形的判定方法三边分别相等两边和它们的夹角分别相等两角和它们的夹边分别相等两角分别相等且其中一组等角的对边相等SSSSASAASASAHL斜边和一条直角边分别相等的两个直角三角形全等两个三角形全等的判定思路两边两角SSSSASHLASAAAS找第三边找两边的夹角看是否是直角三角形找两角的夹边找任意一角的对边两个三角形全等的判定思路一边和它的邻角ASASASAASAASHL找这条边的另一个邻角找这个角的另一边找这条边的对角找另外任意一个角看这个角是否是直角，若是，找任意一条直角边一边一角一边和它的对角角平分线的性质和判定OP平分∠AOB，PD⊥OA于点D，PE⊥OB于点EPD=PEPD⊥OA于点D，PE⊥OB于点E，PD=PEOP平分∠AOB重点梳理如图，已知△ACE≌△DBF．CE=BF，AE=DF，AD=8，BC=2． 解:（1）∵△ACE≌△DBF， ∴AC=BD，则AB=DC， ∵BC=2，∴2AB+2=AD=8， ∴AB=3，∴AC=AB+BC=3+2=5. （2）∵△ACE≌△DBF， ∴∠ECA=∠FBD， ∴CE∥BF． （1）求AC的长度； （2）试说明CE∥BF． 重点梳理总结：全等三角形寻找对应元素的方法对应边公共边一定是对应边长对长，短对短，中对中对应角公共角一定是对应角对顶角一定是对应角大角对大角，小角对小角重点梳理练习1：如图，△ABC≌△DEF，若BC=13，EC=6，则CF=______． 练习2：如图，△ACB≌△A'CB，∠A'CB'=65°， ∠A'CB=35°，则∠ACA'的度数为（ ） ADFCEB7BA. 20° B. 30° C. 35° D. 40° 证明：∵点 B 为线段 AC 的中点， ∴ AB＝ BC ， ∵ AD∥BE ，BD∥CE ， ∴∠A＝∠EBC ，∠C＝∠DBA ， 在△ABD 与△BCE 中， ∠A＝∠EBC， AB＝ BC ， ∠DBA＝∠C ，∴△ ABD ≌△ BCE （ ASA ）． 重点梳理如图， B 是线段 AC 的中点，AD∥BE， BD∥CE ．求证：△ABD≌△BCE ． 重点梳理练习3：已知△ ABC 和△ DEF ，下列条件中，不能保证△ ABC 和△ DEF 全等的是（ ）D A . AB = DE ，AC = DF ，BC = EF B. ∠A =∠D ，∠B =∠E ，AC = DF C. AB = DE ，AC = DF ，∠A =∠D D. AB = DE ，BC = EF ， ∠C =∠F 重点梳理练习4：如图所示，AB 与 CD 相交于点 O ，∠A =∠B ，OA =OB 添加条件__________________________，所以△AOC ≌△BOD 理由是____________. ASA或AAS∠AOC =∠BOD或∠C =∠DD重点梳理练习5：如图，在△ABC 中，AD 平分∠BAC，CE⊥AD 于点 G，交 AB 于点 E ，EF∥BC 交 AC 于点 F，求证：∠DEC =∠FEC . 重点梳理证明： ∵ CE ⊥ AD ，∴ ∠AGE =∠AGC =90 ° 在△ AGE 和△ AGC 中， 在△ DGE 和△ DGC 中， ∴ △ AGE≌△AGC（ASA）∴ GE =GC ∴ △DGE≌△DGC （SAS）. ∴ ∠DEG =∠DCG . ∵ EF//BC ，∴ ∠ FEC = ∠ ECD ， ∴ ∠ DEG = ∠ FEC . 重点梳理如图是小朋友荡秋千的侧面示意图，静止时秋千位于铅垂线BD上，转轴B到地面的距离BD＝2.5m．乐乐在荡秋千过程中，当秋千摆动到最高点A时，测得点A到BD的距离AC＝1.5m，点A到地面的距离AE＝1.5m，当他从A处摆动到A'处时，若A'B⊥AB，求A'到BD的距离．重点梳理解：如图，作A'F⊥BD，垂足为F．∵AC⊥BD，∴∠ACB＝∠A'FB＝90°，在Rt△A'FB中，∠1+∠3＝90°，又∵A'B⊥AB，∴∠1+∠2＝90°，∴∠2＝∠3，在△ACB和△BFA'中，∴△ACB≌△BFA'（AAS），∴A'F＝BC，∵AC∥DE且CD⊥AC，AE⊥DE，∴CD＝AE＝1.5m，∴BC＝BD-CD＝2.5-1.5＝1m，∴A'F＝1m，即A'到BD的距离是1m．∠1∠3∠2重点梳理 练习6：如图，要测量水池的宽度AB，可从点A出发在地面上画一条线段AC，使AC⊥AB，再从点C观测，在BA的延长线上测得一点D，使∠ACD＝∠ACB，这时量得AD＝160m，则水池宽AB的长度是 　 　m．160重点梳理如图，∠1=∠2，点 P 为 BN 上的一点，∠PCB+∠BAP =180 °求证: PA=PC . 重点梳理证明：过点 P 作 PE ⊥ BA，PF ⊥ BC ，垂足分别为 E、F . ∵∠1=∠2， PE⊥BA，PF⊥BC，∴ PE=PF ， ∠PEA =∠PFC =90 °. ∵∠ PCB +∠BAP =180 °又∠ BAP +∠EAP =180 ° ∴ ∠EAP =∠PCB. 在△ APE 和△ CPF 中， ∠ PEA =∠ PFC ， ∠ EAP =∠ FCP ， PE=PF ， ∴ △APE ≌△CPF（AAS）， ∴ AP=CP . 重点梳理练习7：如图，△ABC的三边长分别是6，9，12，其三条角平分线将其分为三个三角形，则S△ABO:S△BCO:S△CAO等于（ ）A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5C重点梳理练习8：如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为51和38，则△EDF的面积为（ ）AA.6.5 B.5.5 C.8 D.13