









所属成套资源:2024年高中数学新高二暑期培优讲义 (2份打包,原卷版+教师版)
2024年高中数学新高二暑期培优讲义第12讲 椭圆(2份打包,原卷版+教师版)
展开
这是一份2024年高中数学新高二暑期培优讲义第12讲 椭圆(2份打包,原卷版+教师版),文件包含2024年高中数学新高二暑期培优讲义第12讲椭圆教师版doc、2024年高中数学新高二暑期培优讲义第12讲椭圆教师版pdf、2024年高中数学新高二暑期培优讲义第12讲椭圆学生版doc、2024年高中数学新高二暑期培优讲义第12讲椭圆学生版pdf等4份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。
题型一:椭圆的定义
题型二:求椭圆的标准方程
题型三:椭圆的综合问题
题型四:轨迹方程
题型五:椭圆的简单几何性质
题型六:求椭圆的离心率
题型七:求椭圆离心率的取值范围
题型八:由椭圆离心率求参数的取值范围
题型九:椭圆中的范围与最值问题
题型十:焦点三角形
【知识点梳理】
知识点一:椭圆的定义
平面内一个动点 SKIPIF 1 < 0 到两个定点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的距离之和等于常数( SKIPIF 1 < 0 ),这个动点 SKIPIF 1 < 0 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.
知识点诠释:
若 SKIPIF 1 < 0 ,则动点 SKIPIF 1 < 0 的轨迹为线段 SKIPIF 1 < 0 ;
若 SKIPIF 1 < 0 ,则动点 SKIPIF 1 < 0 的轨迹无图形.
知识点二:椭圆的标准方程
1、当焦点在 SKIPIF 1 < 0 轴上时,椭圆的标准方程: SKIPIF 1 < 0 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 ;
2、当焦点在 SKIPIF 1 < 0 轴上时,椭圆的标准方程: SKIPIF 1 < 0 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 ;
知识点诠释:
(1)这里的“标准”指的是中心在坐标原点,对称轴为坐标轴建立直角坐标系时,才能得到椭圆的标准方程;
(2)在椭圆的两种标准方程中,都有 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ;
(3)椭圆的焦点总在长轴上.当焦点在 SKIPIF 1 < 0 轴上时,椭圆的焦点坐标为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;当焦点在 SKIPIF 1 < 0 轴上时,椭圆的焦点坐标为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
(4) 在两种标准方程中,∵a2>b2,∴可以根据分母的大小来判定焦点在哪一个坐标轴上.
知识点三:求椭圆的标准方程
求椭圆的标准方程主要用到以下几种方法:
(1)待定系数法:①若能够根据题目中条件确定焦点位置,可先设出标准方程,再由题设确定方程中的参数a,b,即:“先定型,再定量”.②由题目中条件不能确定焦点位置,一般需分类讨论;有时也可设其方程的一般式: SKIPIF 1 < 0 .
(2)定义法:先分析题设条件,判断出动点的轨迹,然后根据椭圆的定义确定方程,即“先定型,再定量”。利用该方法求标准方程时,要注意是否需先建立平面直角坐标系再解题.
知识点四:椭圆的简单几何性质
我们根据椭圆 SKIPIF 1 < 0 SKIPIF 1 < 0 来研究椭圆的简单几何性质
椭圆的范围
椭圆上所有的点都位于直线x=±a和y=±b所围成的矩形内,所以椭圆上点的坐标满足|x|≤a,|y|≤b.
椭圆的对称性
对于椭圆标准方程 SKIPIF 1 < 0 ,把x换成-x,或把y换成-y,或把x、y同时换成-x、-y,方程都不变,所以椭圆 SKIPIF 1 < 0 是以x轴、y轴为对称轴的轴对称图形,且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
椭圆的顶点
①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
②椭圆 SKIPIF 1 < 0 (a>b>0)与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)。
③线段A1A2,B1B2分别叫做椭圆的长轴和短轴,|A1A2|=2a,|B1B2|=2b。a和b分别叫做椭圆的长半轴长和短半轴长。
椭圆的离心率
①椭圆的焦距与长轴长度的比叫做椭圆的离心率,用e表示,记作 SKIPIF 1 < 0 .
②因为a>c>0,所以e的取值范围是0<e<1。e越接近1,则c就越接近a,从而 SKIPIF 1 < 0 越小,因此椭圆越扁;反之,e越接近于0,c就越接近0,从而b越接近于a,这时椭圆就越接近于圆。当且仅当a=b时,c=0,这时两个焦点重合,图形变为圆,方程为x2+y2=a2。
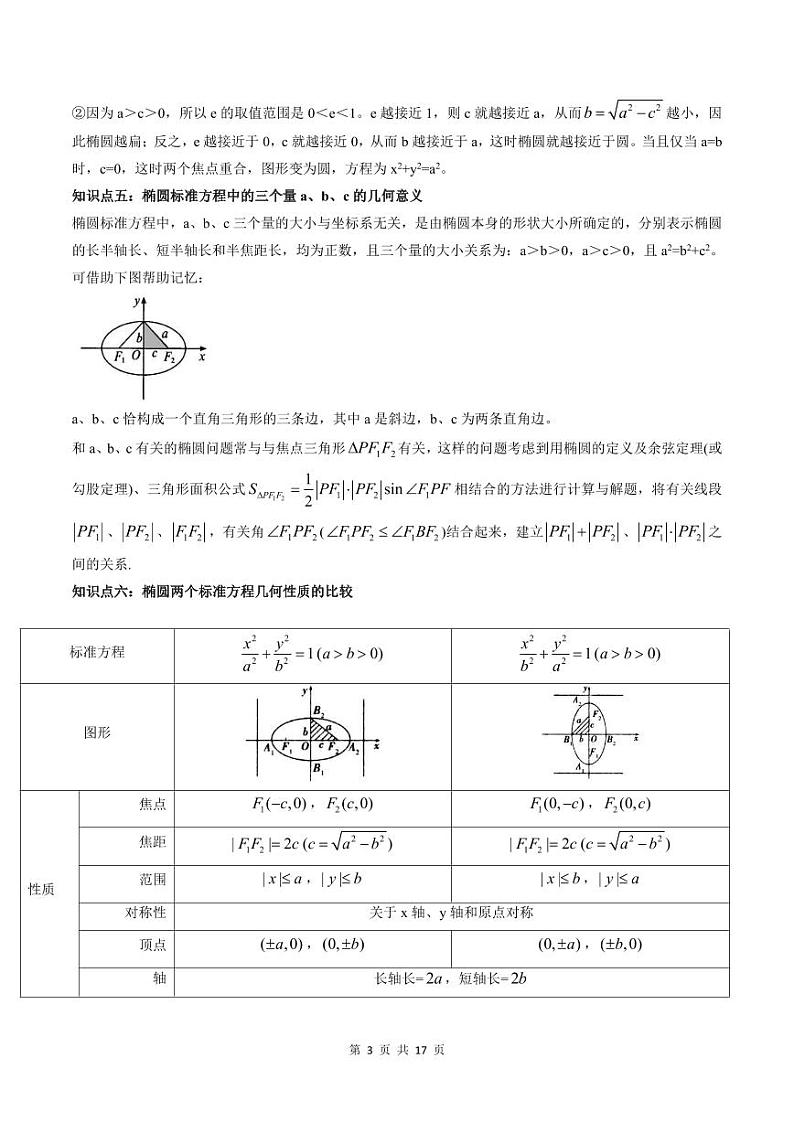
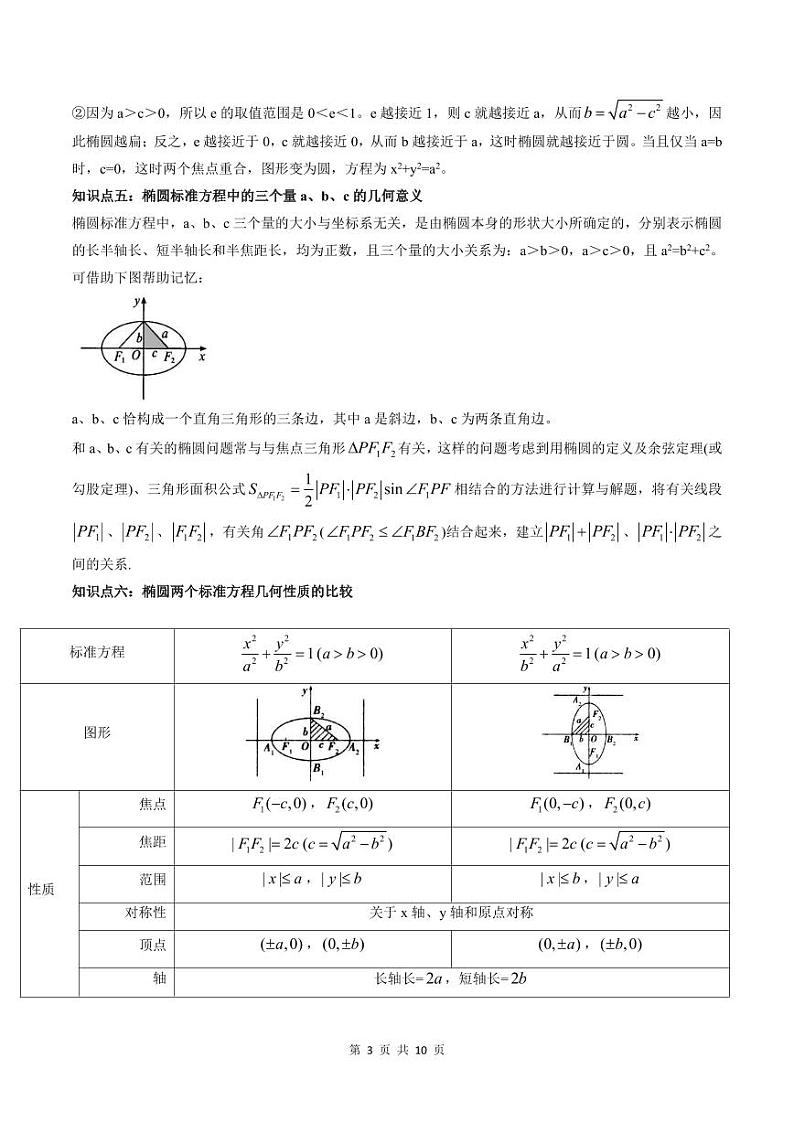
知识点五:椭圆标准方程中的三个量a、b、c的几何意义
椭圆标准方程中,a、b、c三个量的大小与坐标系无关,是由椭圆本身的形状大小所确定的,分别表示椭圆的长半轴长、短半轴长和半焦距长,均为正数,且三个量的大小关系为:a>b>0,a>c>0,且a2=b2+c2。
可借助下图帮助记忆:
a、b、c恰构成一个直角三角形的三条边,其中a是斜边,b、c为两条直角边。
和a、b、c有关的椭圆问题常与与焦点三角形 SKIPIF 1 < 0 有关,这样的问题考虑到用椭圆的定义及余弦定理(或勾股定理)、三角形面积公式 SKIPIF 1 < 0 相结合的方法进行计算与解题,将有关线段 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,有关角 SKIPIF 1 < 0 ( SKIPIF 1 < 0 )结合起来,建立 SKIPIF 1 < 0 、 SKIPIF 1 < 0 之间的关系.
知识点六:椭圆两个标准方程几何性质的比较
知识点诠释:椭圆 SKIPIF 1 < 0 , SKIPIF 1 < 0 (a>b>0)的相同点为形状、大小都相同,参数间的关系都有a>b>0和 SKIPIF 1 < 0 ,a2=b2+c2;不同点为两种椭圆的位置不同,它们的焦点坐标也不相同;
椭圆的焦点总在长轴上,因此已知标准方程,判断焦点位置的方法是:看x2、y2的分母的大小,哪个分母大,焦点就在哪个坐标轴上。
【典例例题】
题型一:椭圆的定义
例1.设定点 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,动点P满足条件 SKIPIF 1 < 0 ,则点P的轨迹是( )
A.椭圆B.线段C.不存在D.椭圆或线段
例2.设 SKIPIF 1 < 0 分别为椭圆 SKIPIF 1 < 0 的左右焦点,过 SKIPIF 1 < 0 的直线交椭圆于A、B两点,则 SKIPIF 1 < 0 的周长为( )
A.12B.24C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
题型二:求椭圆的标准方程
例3.已知椭圆 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 ,过坐标原点的直线交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 两点,且 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,则椭圆 SKIPIF 1 < 0 的标准方程为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例4.求满足下列条件的椭圆的标准方程:
(1)焦点坐标分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,经过点 SKIPIF 1 < 0 ;
(2)焦点在 SKIPIF 1 < 0 轴上的椭圆上任意一点到两个焦点的距离的和为 SKIPIF 1 < 0 .
题型三:椭圆的综合问题
例5.已知椭圆的方程为 SKIPIF 1 < 0 ,若点P在椭圆上,F1,F2为椭圆的两个焦点,且 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的面积.
例6.已知椭圆 SKIPIF 1 < 0 的长轴长是短轴长的 SKIPIF 1 < 0 倍,且椭圆C经过点 SKIPIF 1 < 0 .
(1)求椭圆C的方程;
(2)设O为坐标原点,过右焦点F的直线l与椭圆C交于A,B两点.求使 SKIPIF 1 < 0 面积最大时直线l的方程.
例7.已知椭圆 SKIPIF 1 < 0 的焦点在 SKIPIF 1 < 0 轴上,长轴长为4,离心率 SKIPIF 1 < 0 .
(1)求椭圆的标准方程;
(2)直线 SKIPIF 1 < 0 : SKIPIF 1 < 0 与椭圆有两个交点,求实数 SKIPIF 1 < 0 的取值范围.
题型四:轨迹方程
例8.已知动圆过定点 SKIPIF 1 < 0 ,并且在定圆B: SKIPIF 1 < 0 的内部与其相切,则动圆圆心的轨迹方程是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例9.在 SKIPIF 1 < 0 中,已知 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,且满足 SKIPIF 1 < 0 ,则顶点 SKIPIF 1 < 0 的轨迹方程是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例10.设 SKIPIF 1 < 0 为坐标原点,动点 SKIPIF 1 < 0 在椭圆C: SKIPIF 1 < 0 上,过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴的垂线,垂足为 SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ,则点 SKIPIF 1 < 0 的轨迹方程是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例11.已知圆 SKIPIF 1 < 0 ,圆 SKIPIF 1 < 0 ,动圆M与圆 SKIPIF 1 < 0 外切,同时与圆 SKIPIF 1 < 0 内切,则动圆圆心M的轨迹方程为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
题型五:椭圆的简单几何性质
例12.已知椭圆 SKIPIF 1 < 0 的左、右焦点分别为点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,若椭圆上顶点为点 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 为等腰直角三角形,则 SKIPIF 1 < 0 ______.
例13.椭圆 SKIPIF 1 < 0 的内接正方形的周长为__________.
题型六:求椭圆的离心率
例14.椭圆 SKIPIF 1 < 0 : SKIPIF 1 < 0 的左焦点为 SKIPIF 1 < 0 ,右焦点为 SKIPIF 1 < 0 ,以 SKIPIF 1 < 0 为圆心, SKIPIF 1 < 0 为半径的圆与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的离心率为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例15.椭圆 SKIPIF 1 < 0 的半焦距为c,若直线y=2x与椭圆的一个交点的横坐标恰为c,则椭圆的离心率为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 -1C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例16.已知椭圆 SKIPIF 1 < 0 : SKIPIF 1 < 0 ( SKIPIF 1 < 0 )的左右焦点分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 , SKIPIF 1 < 0 为椭圆上一点, SKIPIF 1 < 0 ,若坐标原点 SKIPIF 1 < 0 到 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 ,则椭圆离心率为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
题型七:求椭圆离心率的取值范围
例17.已知F1,F2分别是椭圆 SKIPIF 1 < 0 + SKIPIF 1 < 0 =1(a>b>0)的左、右焦点,若椭圆上存在点P,使∠F1PF2=90°,则椭圆的离心率e的取值范围为 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例18.已知 SKIPIF 1 < 0 是椭圆 SKIPIF 1 < 0 的左右焦点,椭圆上一点M满足: SKIPIF 1 < 0 ,则该椭圆离心率取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
例19.已知椭圆 SKIPIF 1 < 0 的左右焦点分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,若椭圆上存在点 SKIPIF 1 < 0 ,使 SKIPIF 1 < 0 ,则该椭圆离心率的取值范围为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
题型八:由椭圆离心率求参数的取值范围
例20.已知椭圆C的离心率为 SKIPIF 1 < 0 ,则椭圆C的长轴长与短轴长的比值为______.
例21.已知椭圆 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,右顶点为 SKIPIF 1 < 0 ,且离心率为 SKIPIF 1 < 0 ,求短轴长为______.
题型九:椭圆中的范围与最值问题
例22.已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 是椭圆 SKIPIF 1 < 0 的两个焦点,点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上,则 SKIPIF 1 < 0 的最大值为_______.
例23.已知椭圆 SKIPIF 1 < 0 的离心率为 SKIPIF 1 < 0 , SKIPIF 1 < 0 为椭圆 SKIPIF 1 < 0 上的一个动点,定点 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最大值为______.
例24.已知椭圆 SKIPIF 1 < 0 : SKIPIF 1 < 0 的右焦点F,点Р在椭圆C上,又点 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最小值为___________.
题型十:焦点三角形
例25.已知椭圆 SKIPIF 1 < 0 的两个焦点是 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,M是此椭圆上一点,且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的面积为______.
例26.设 SKIPIF 1 < 0 , SKIPIF 1 < 0 是椭圆 SKIPIF 1 < 0 的两个焦点,P是椭圆上的点,且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的面积为________.
例27.椭圆 SKIPIF 1 < 0 的两个焦点为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,点P在椭圆C上,且 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则椭圆C的方程为___________.
【过关测试】
一、单选题
1.中心在原点,焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.椭圆 SKIPIF 1 < 0 中,点 SKIPIF 1 < 0 为椭圆的右焦点,点A为椭圆的左顶点,点B为椭圆的短轴上的顶点,若 SKIPIF 1 < 0 ,此椭圆称为“黄金椭圆”,“黄金椭圆”的离心率为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
3.已知P点是椭圆 SKIPIF 1 < 0 上的动点,A点坐标为 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最小值为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
4.已知点P为椭圆 SKIPIF 1 < 0 上动点, SKIPIF 1 < 0 分别是椭圆C的焦点,则 SKIPIF 1 < 0 的最大值为( )
A.2B.3C. SKIPIF 1 < 0 D.4
二、填空题
5.椭圆的一个焦点到长轴两端点的距离之比为 SKIPIF 1 < 0 ,短轴长为8,则椭圆的标准方程为____________________.
6.椭圆 SKIPIF 1 < 0 的焦点为 SKIPIF 1 < 0 ,点P是椭圆上任意一点,当 SKIPIF 1 < 0 时,P点横坐标的取值范围是__________.
7.已知 SKIPIF 1 < 0 分别为椭圆 SKIPIF 1 < 0 的左、右焦点,点P在椭圆上, SKIPIF 1 < 0 (O为坐标原点)是面积为 SKIPIF 1 < 0 的正三角形,则此椭圆的方程为__________.
三、解答题
8.已知点P是椭圆 SKIPIF 1 < 0 上的一点, SKIPIF 1 < 0 和 SKIPIF 1 < 0 分别为左右焦点,焦距为6,且过 SKIPIF 1 < 0 .
(1)求椭圆的标准方程;
(2)若动直线l过 SKIPIF 1 < 0 与椭圆交于A、B两点,求 SKIPIF 1 < 0 的周长.
9.已知椭圆 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 SKIPIF 1 < 0 在椭圆上, SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 的周长为6,面积为 SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的标准方程;
(2)过点 SKIPIF 1 < 0 的直线 SKIPIF 1 < 0 交椭圆于 SKIPIF 1 < 0 两点,交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 点,设 SKIPIF 1 < 0 ,试判断 SKIPIF 1 < 0 是否为定值?请说明理由.
标准方程
SKIPIF 1 < 0
SKIPIF 1 < 0
图形
性质
焦点
SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 , SKIPIF 1 < 0
焦距
SKIPIF 1 < 0
SKIPIF 1 < 0
范围
SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 , SKIPIF 1 < 0
对称性
关于x轴、y轴和原点对称
顶点
SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 , SKIPIF 1 < 0
轴
长轴长= SKIPIF 1 < 0 ,短轴长= SKIPIF 1 < 0
离心率
SKIPIF 1 < 0
相关试卷
这是一份2024年高中数学新高二暑期培优讲义第9讲 直线的交点坐标与距离公式(2份打包,原卷版+教师版),文件包含2024年高中数学新高二暑期培优讲义第9讲直线的交点坐标与距离公式教师版doc、2024年高中数学新高二暑期培优讲义第9讲直线的交点坐标与距离公式教师版pdf、2024年高中数学新高二暑期培优讲义第9讲直线的交点坐标与距离公式学生版doc、2024年高中数学新高二暑期培优讲义第9讲直线的交点坐标与距离公式学生版pdf等4份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
这是一份2024年高中数学新高二暑期培优讲义第06讲 空间向量的应用(2份打包,原卷版+教师版),文件包含2024年高中数学新高二暑期培优讲义第06讲空间向量的应用教师版doc、2024年高中数学新高二暑期培优讲义第06讲空间向量的应用教师版pdf、2024年高中数学新高二暑期培优讲义第06讲空间向量的应用学生版doc、2024年高中数学新高二暑期培优讲义第06讲空间向量的应用学生版pdf等4份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
这是一份2024年高中数学新高二暑期培优讲义第05讲 空间向量及其运算的坐标表示(2份打包,原卷版+教师版),文件包含2024年高中数学新高二暑期培优讲义第05讲空间向量及其运算的坐标表示教师版doc、2024年高中数学新高二暑期培优讲义第05讲空间向量及其运算的坐标表示教师版pdf、2024年高中数学新高二暑期培优讲义第05讲空间向量及其运算的坐标表示学生版doc、2024年高中数学新高二暑期培优讲义第05讲空间向量及其运算的坐标表示学生版pdf等4份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。









