2024徐州中考数学二轮重点专题研究 第12课时 反比例函数（课件）

这是一份2024徐州中考数学二轮重点专题研究 第12课时 反比例函数（课件），共34页。PPT课件主要包含了第4题图，第5题图，第6题图，第7题图，第9题图，第9题解图，反比例函数，考点精讲，图象及性质，表达式等内容，欢迎下载使用。

反比例函数的图象与性质
1. (2019徐州7题3分)若A(x1，y1)、B(x2，y2)都在函数y＝ 的图象上，且x1＜0＜x2，则(　　)A. y1＜y2　　　B. y1＝y2　　　C. y1＞y2　　　D. y1＝－y2
反比例函数解析式的确定2. (2017徐州12题3分)反比例函数y＝ 的图象经过点M(－2，1)，则k＝________．3. (2016徐州11题3分)若反比例函数的图象过点(3，－2)，则其函数表达式为________．
k的几何意义(10年2考)
4. (2020徐州7题3分)如图，在平面直角坐标系中，函数y＝kx与y＝－ 的图象交于A、B两点，过点A作y轴的垂线，交函数y＝ 的图象于点C，连接BC，则△ABC的面积为(　　)A. 2 B. 4 C. 6 D. 8
5. (2021徐州17题3分)如图，点A、D分别在函数y＝ 、y＝ 的图象上，点B、C在x轴上．若四边形ABCD为正方形，点D在第一象限，则D的坐标是__________．
反比例函数与一次函数结合(10年4考)
6. (2023徐州7题3分)如图，在平面直角坐标系xOy中，函数y＝kx＋b (k≠0)与y＝ (m≠0)的图象相交于点A(2，3)，B(－6，－1)，则不等式kx＋b＞ 的解集为(　　)A. x＜－6 B. －6＜x＜0或x＞2C. x＞2 D. x＜－6或0＜x＜2
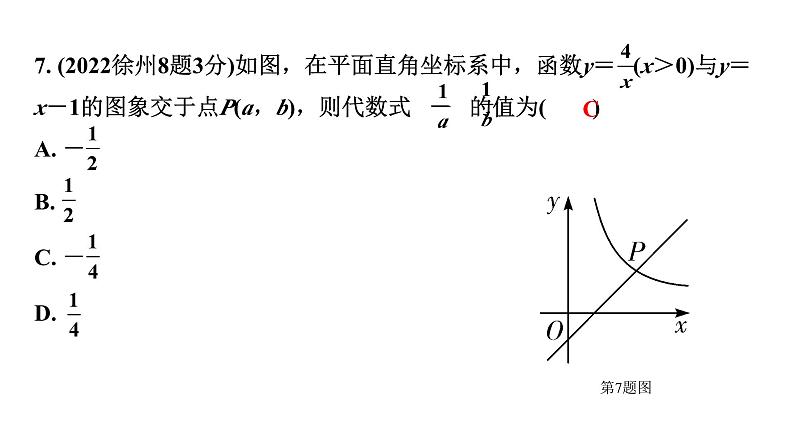
7. (2022徐州8题3分)如图，在平面直角坐标系中，函数y＝ (x＞0)与y＝x－1的图象交于点P(a，b)，则代数式 － 的值为(　　)A. － B. C. － D.
8. (2012徐州13题3分)正比例函数y＝k1x的图象与反比例函数y＝ 的图象相交于点(1，2)，则k1＋k2＝_______．
9.如图，在平面直角坐标系中，一次函数y＝kx＋b的图象经过点A(0，－4)，B(2，0)，交反比例函数y＝ (x＞0)的图象于点G(3，a)，点P在反比例函数的图象上，横坐标为n(0＜n＜3)，PQ∥y轴交直线AB于点Q，D是y轴上任意一点，连接PD、QD. (1)求一次函数和反比例函数的表达式；
(2)求△DPQ面积的最大值．
(3)在(2)的条件下，在y轴上找一点D，使DP＋DQ的值最小，求满足条件的点D的坐标．
(3)由(2)知△DPQ面积最大时，点P坐标为(1，6)，点Q坐标为(1，－2)，如解图，过点P作P关于y轴的对称点P′，连接P′Q，交y轴于点D，此时DP＋DQ的值最小，∴P′(－1，6)，设直线P′Q的表达式为y＝kx＋b，将P′(－1，6)，Q(1，－2)代入y＝kx＋b，解得b＝2，k＝－4，∴直线P′Q的表达式为y＝－4x＋2，当x＝0时，y＝2，∴点D的坐标为(0，2)．
【对接教材】八下第11章P122－P145
定义：一般地，形如y＝ (k为常数，k≠0)的函数叫做反比例函数．其中x是自变量，y是x的函数，且x≠0
y= (k 为常数,k≠0)
图象无限接近坐标轴,但不与坐标轴相交
第_______象限(x,y 同号)
第_______象限(x,y 异号)
反比例函数图象的位置和增减性都与k的符号有关，反比例函数的增减性只能在每个象限内讨论
k 的几何意义及其相关计算
1.k 的几何意义:如图,在反比例函数y= (k<0)的图象上任取一点P(x,y), 过这一点分别作x 轴、y 轴的垂线,PM、PN 与坐标轴围成的矩形PMON 的面积S=|xy|=___________________________________. 2.常见图形及面积计算(用|k|表示)
S△AOP = ____________ .
S△APB =__________.
S△APP'=_____(P'为P 关于原点的对称点)
S△APP'=_____(P'为P 关于原点 的对称点)
利用k的几何意义：由系数k的几何意义(一般是图形面积)求出|k|，先根据函数图象所在象限判断k的符号，确定k的值，再将k代入y＝ 确定解析式
1.设所求反比例函数的解析式为y＝ (k≠0)2.根据已知条件，得到反比例函数图象上一个点的坐标P(a，b)3.将点P的坐标代入所设的解析式得到系数k＝ab4.写出函数解析式
例1 已知反比例函数y＝ (a≠0)．(1)若反比例函数y＝ (a≠0)的图象在每一个象限内，y都随x的增大而增大，则a的取值范围是________；(2)若点P(m，n)在反比例函数图象上，则点Q (－m，－n)________该反比例函数图象上(填“在”或“不在”)；(3)若反比例函数的图象分布在第一、三象限，则a的取值范围是______；
(4)若点(－2，y1)，(2，y2)，(3，y3)在函数y＝ (a>0)的图象上，则y1，y2，y3的大小关系为____________(用“>”连接)；
(5)若点(3，－3)在反比例函数y＝ 的图象上，则反比例函数的解析式为______________，当－2≤x≤－1时，y的最小值为________；(6)如图，若▱ABCD的边AB在x轴上，点D在反比例函数y＝ (a≠0，x>0)的图象上，若S▱ABCD＝4，则a＝________．
例2 如图①，反比例函数y＝ (x>0)与一次函数y＝kx＋b的图象交于A(1，6)，B(3，n)两点，一次函数y＝kx＋b交y轴于点C，交x轴于点D.
(1)求反比例函数和一次函数的解析式；
(2)结合图象，写出当kx＋b> 时，x的取值范围；
(3)连接OA，OB，求△AOB的面积；
(4)若点P在x轴，且S△PCD＝3S△OAB，请你求出所有符合条件的点P的坐标；
(5)将一次函数的图象向下平移至与反比例函数图象在第一象限只有一个交点的位置，求此时一次函数的表达式；
(6)(核心考法)如图②，若直线y＝t(n＜t＜6)与该反比例函数的图象交于点E，与直线AB交于点F，求△OEF面积的最大值．
1. 如图，在平面直角坐标系中，一次函数y＝mx＋n的图象与反比例函数y＝ 的图象相交于A(－1，3)、B(3，b)两点，与y轴相交于点C.
(1)求一次函数和反比例函数的表达式；