2024徐州中考数学二轮重点专题研究 第23课时 矩形（课件）

这是一份2024徐州中考数学二轮重点专题研究 第23课时 矩形（课件），共21页。PPT课件主要包含了考点精讲等内容，欢迎下载使用。

与矩形有关的证明及计算
1.如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点,若MN=4, 则AC的长为 .
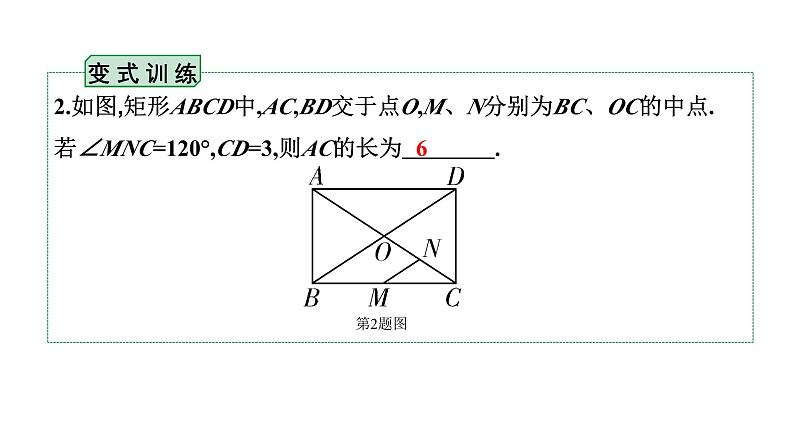
2.如图,矩形ABCD中,AC,BD交于点O,M、N分别为BC、OC的中点.若∠MNC=120°,CD=3,则AC的长为 .
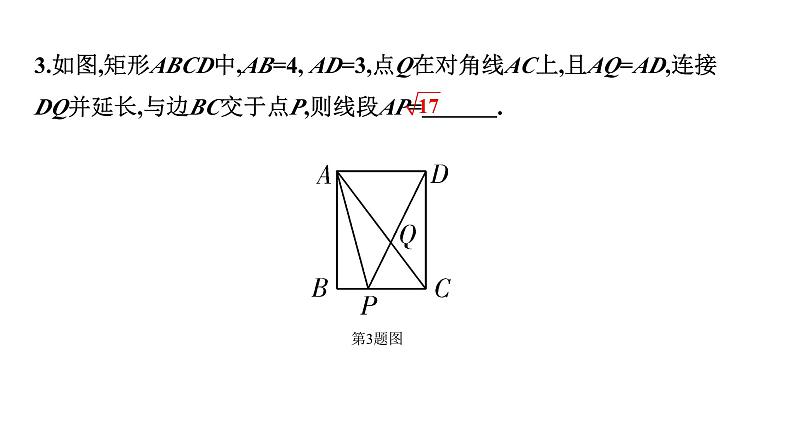
3.如图,矩形ABCD中,AB=4, AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
4.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD、EC.(1)求证:四边形BECD是平行四边形;
(1)证明：∵四边形ABCD是平行四边形，∴BC∥AD，BC＝AD，∴△EBO∽△EAD，(1分)∴ ，∵O是BC的中点，∴BO＝ BC＝ AD，(3分)∴EO＝ ED，即点O是ED的中点，∴四边形BECD是平行四边形(对角线互相平分的四边形是平行四边形)；(5分)
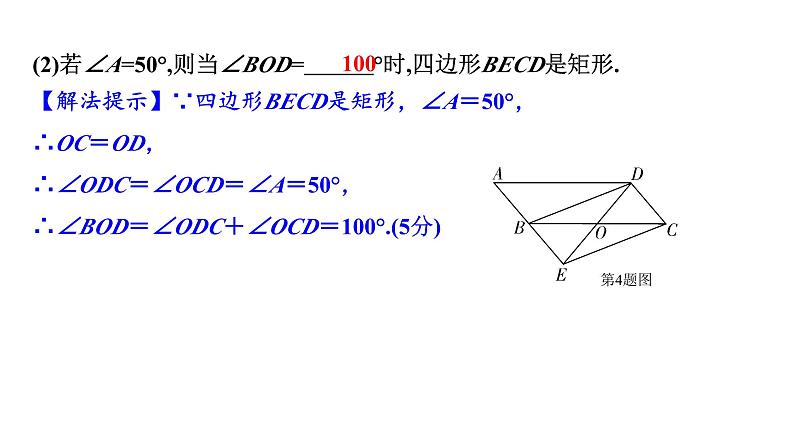
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.
【解法提示】∵四边形BECD是矩形，∠A＝50°，∴OC＝OD，∴∠ODC＝∠OCD＝∠A＝50°，∴∠BOD＝∠ODC＋∠OCD＝100°.(5分)
【对接教材】苏科:八下第9章P74-P77
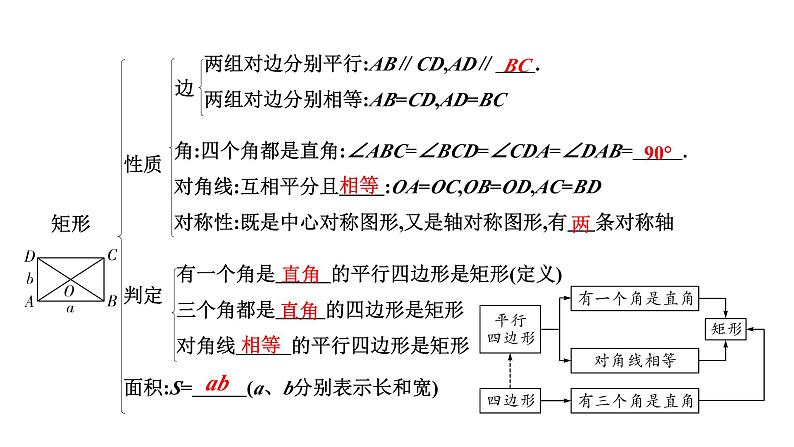
两组对边分别平行:AB∥CD,AD∥ .两组对边分别相等:AB=CD,AD=BC
角:四个角都是直角:∠ABC=∠BCD=∠CDA=∠DAB= .对角线:互相平分且 :OA=OC,OB=OD,AC=BD 对称性:既是中心对称图形,又是轴对称图形,有 条对称轴
有一个角是 的平行四边形是矩形(定义) 三个角都是 的四边形是矩形 对角线 的平行四边形是矩形
面积:S= (a、b分别表示长和宽)
例1 如图,在矩形ABCD中,对角线AC与BD相交于点O, AB=6.
(1)若BC=8,则BD的长为 ; (2)若∠AOD=120°. ①∠ACB的度数为 ; ②矩形ABCD的面积为 ; ③矩形ABCD的周长为 .
例2 在四边形ABCD中,AB∥CD. (1)如图①,AB=CD,∠A=90°,求证:四边形ABCD是矩形;
(1)证明：∵AB ∥CD，AB＝CD，∴四边形ABCD是平行四边形．∵∠A＝90°，∴平行四边形ABCD是矩形；
(1)【判定依据】判定矩形的依据是______________________________________________________________
有一个角是直角的平行四边形是矩形．
(2)如图②,AB=CD,对角线AC、BD交于点O,且∠OAB=∠OBA,求证:四边形ABCD是矩形;
(2)∵AB ∥CD，AB ＝CD，∴四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵∠OAB＝∠OBA，∴OA ＝ OB，∴AC＝ BD，∴平行四边形ABCD是矩形；
(2)【判定依据】判定矩形的依据是______________________________________________________________
对角线相等的平行四边形是矩形．
(3)如图③,连接AC,延长AD到点E,使ED=DA,连接EC并延长,若EC= CA,CB平分△EAC的外角.求证:四边形ABCD是矩形.
(3)∵ED＝DA，EC＝CA，∴CD⊥AE，CD平分∠ECA，∵AB∥CD，∴∠CDA＝∠BAD＝90°，又∵CB平分△EAC的外角，∴∠DCB＝∠DCA＋∠ACB＝ ×180°＝90°，∴∠CDA＝∠BAD＝∠DCB＝90°，∴四边形ABCD是矩形．
(3)【判定依据】判定矩形的依据是______________________________________________________________
有三个角是直角的四边形是矩形．
例3 如图,在矩形ABCD中,点E、F分别在AD、BC边上,连接BE,EF,DF. (1)如图①,当AE=CF时,求证:BE∥DF;
(1)【判定依据】判定BE∥DF的依据是______________________________________________________________
平行四边形的对边平等且相等
证法二：∵四边形ABCD是矩形，∴AD＝BC，AD∥BC，∠A＝∠C＝90°，∴∠AEB＝∠EBC.在△ABE和△CDF中，∴△ABE≌△CDF(SAS)，∴∠AEB＝∠CFD，∴∠EBC＝∠DFC，∴BE∥DF；
AB=CD∠A=∠CAE=CF
(2)如图②,已知AB=4,AD=8,且点B与点D关于EF对称. ①求证:四边形BEDF为菱形;
∵点B与点D关于EF对称，∴EF⊥BD，OB＝OD.∵四边形ABCD是矩形，∴AD∥BC，∴∠EDO＝∠FBO.在△ODE和△OBF中，
∠EDO＝∠FBOOD=OB∠DOE＝∠BOF
①证明：证法一：如图，连接BD，交EF于点O，
∴△ODE≌△OBF(ASA)，∴DE＝BF，∴四边形BEDF是平行四边形．∵EF⊥BD，∴平行四边形BEDF是菱形；
(2)【判 定 依 据】判定菱形的依据_____________________________________________________________
对角线互相垂直的平行四边形是菱形．
∵点B与点D关于EF对称，∴点O是矩形ABCD的对称中心，且EF垂直平分BD，∵四边形ABCD是矩形，∴DE∥BF，又∵DE＝BF(证法同证法一)，∴四边形BEDF是平行四边形，∵EF垂直平分BD，∴平行四边形BEDF是菱形；
证法二：如解图，连接BD，交EF于点O，
②BE= ,EF= .
1. 如图,在▱ABCD中,AB⊥BD,E为AB边的中点,点F为DE延长线上一点,且∠AFB=90°,过点B作BG∥AF交DE于点G,连接AG.(1)判断四边形AFBG的形状,并说明理由;
解：(1)四边形AFBG为矩形，理由如下：∵BG∥AF，∴∠BGE＝∠AFE，∵点E为AB的中点，∴BE＝AE，∵∠BEG＝∠AEF，∴△BEG≌△AEF(AAS)，∴BG＝AF，∴四边形AFBG为平行四边形，∵∠AFB＝90°，∴平行四边形AFBG为矩形；