2024徐州中考数学二轮重点专题研究 微专题 运动产生的特殊三角形问题（含菱形）（课件）

这是一份2024徐州中考数学二轮重点专题研究 微专题 运动产生的特殊三角形问题（含菱形）（课件），共36页。PPT课件主要包含了例1题图③，例1题图②，例1题图④，例2题图①，例2题图②，例2题解图，例2题图③，例2题图④，例3题图①，例3题图②等内容，欢迎下载使用。

【作法提示】①以点A为圆心，AB长为半径画圆，交直线l于P1，P2两点；②以点B为圆心，AB长为半径画圆，交直线l于点P3；③连接以上两圆的交点作AB的垂直平分线，直线与l的交点即为P4.
(2)如图②，在平面直角坐标系中，点A的坐标为(2，3)，在x轴正半轴上有一点B，使△AOB为等腰三角形，且BA＝BO，则点B的坐标为________．(3)如图③，在平面直角坐标系中，已知点A(2，2)，B(4，0)，若在y轴上取一点C，使△ABC为等腰三角形，则点C的坐标为______________．
(0，0)或(0，－2)
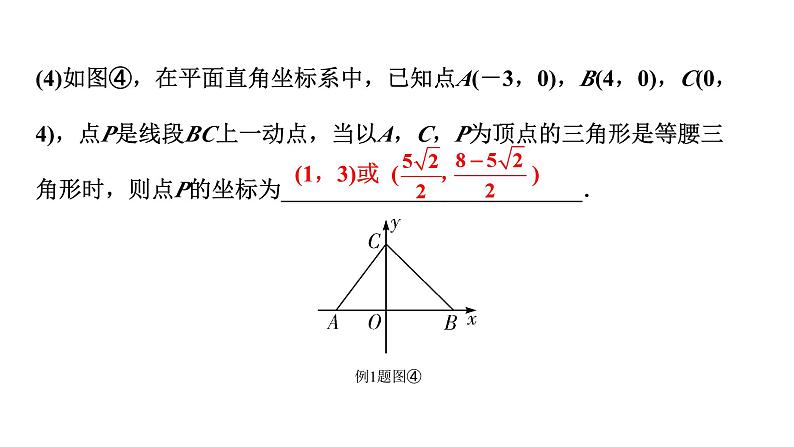
(4)如图④，在平面直角坐标系中，已知点A(－3，0)，B(4，0)，C(0，4)，点P是线段BC上一动点，当以A，C，P为顶点的三角形是等腰三角形时，则点P的坐标为__________________________．
1. 确定点的位置：已知线段AB，在平面内找一点P，使得△ABP为等腰三角形，这样的点P位置有以下两种情况：(1)以AB为腰：点P在分别以点A、B为圆心，AB长为半径的圆上，AB直线上的点除外；(2)以AB为底：点P在AB的垂直平分线上，AB直线上的点除外．
2. 求点P坐标的方法如下：分别表示出点A、B、P的坐标，再根据勾股定理表示出线段AB、BP、AP的长度，由①AB＝AP，②AB＝BP，③BP＝AP列方程解出坐标．
【思维教练】由于点A、B、D三点的坐标确定，可根据勾股定理分别计算出三条线段的长，进行比较分析即可．
解：(1)△ABD为等腰三角形．理由如下：∵A(－1，0)，B(3，0)，D(0， )，∴AD＝ ＝2 ，BD＝ ＝4，AB＝3＋1＝4，∴AB＝BD，∴△ABD是等腰三角形；
(2)在抛物线上是否存在一点P，使得△PCO是以OC为底的等腰三角形，若存在，请你求出点P的横坐标；若不存在，请说明理由；
【思维教练】由于点P在抛物线上，△PCO是以OC为底的等腰三角形，所以点P在OC的垂直平分线上，即点P的纵坐标为1，将y＝1代入抛物线表达式求解即可．
(2)存在．点P的横坐标为1＋ 或1－ ；如解图，作CO的垂直平分线交抛物线于点P和点P′，交CO于点D.连接CP，OP，OP′，CP′，则△POC和△P′CO是以OC为底的等腰三角形．令x＝0，则y＝2，∴C(0，2)，∴OC＝2.∵△COP是以CO为底的等腰三角形，C(0，2)，∴CD＝DO＝1，当y＝1时，－ x2＋ x＋2＝1，
解得x＝1＋ 或x＝1－ ，∴点P的横坐标为1＋ ，点P′的横坐标为1－ .即存在点P使得△PCO是以OC为底的等腰三角形，点P的横坐标为1＋ 或1－ .
(3)在抛物线的对称轴上是否存在点Q，使得△BMQ是以BQ为腰的等腰三角形，若存在，请你求出点Q的坐标；若不存在，请说明理由；
【思维教练】分BQ＝QM和BQ＝MB两种情况，利用点的坐标即可求解．
(3)存在．∵y＝－ x2＋ x＋2，∴抛物线对称轴为直线x＝－ ＝1，点B的坐标为(3，0)，M(1， )．设点Q的坐标为 Q(1，t)，∴BQ＝ ，QM＝| －t|，MB＝ ＝ .∵△BMQ 是以 BQ 为腰的等腰三角形，∴分两种情况讨论：
(4)在x轴上是否存在一点E，使得△ACE是等腰三角形，若存在，请你求出点E的横坐标；若不存在，请说明理由．
【思维教练】先设出点 E的坐标， 由于△ACE是等腰三角形，可分为三种情况讨论：①AE＝AC, ②AC＝CE，③AE＝CE，当AE＝AC时还要注意点E分别在点A的两侧两种情况．
考向二　运动产生的直角三角形问题
例3　(1)如图①，线段AB在直线l上方，在直线l上是否存在一点P，使△PAB是直角三角形？请在图中画出所有符合条件要求的点P，并说明画图依据；
解：(1)存在点P，使△PAB是直角三角形，如解图中点P1，P2，P3，P4即为满足条件的点P.
画图依据：①AB作为直角边：分别过点A，B作线段AB的垂线，交直线l于点P1，P2；②AB作为斜边：以AB为直径画圆，交直线l于点P3，P4，根据直径所对的圆周角是直角得到直角三角形．
(2)如图②，在平面直角坐标系中，点A，B的坐标分别是(3，0)，(0，4)．点P为y轴上一点，使△PAB为直角三角形，求点P的坐标；
②当AB为斜边时，同理可得AB2＝AP2＋BP2，即25＝9＋p2＋(4－p)2，解得p＝0或p＝4(不符合题意，舍去)，∴P(0，0)．综上所述，点P的坐标为(0，－ )或(0，0)．
(3)如图③，在平面直角坐标系中，已知点A(－5，0)，B(0，－5)，在直线x＝－3上取点C，使得△ABC为直角三角形，求满足条件的点C的坐标．
(3)∵点C在直线x＝－3上，∴设C(－3，y)，∵A(－5，0)，B(0，－5)，∴AB2＝50，AC2＝4＋y2，BC2＝9＋(y＋5)2＝y2＋10y＋34，分三种情况讨论：
①当∠ACB＝90°时，则AB2＝AC2＋BC2，即50＝4＋y2＋y2＋10y＋34，解得y＝－6或y＝1，此时点C的坐标为(－3，－6)或(－3，1)；②当∠ABC＝90°时，则AC2＝AB2＋BC2，即4＋y2＝50＋y2＋10y＋34，解得y＝－8，此时点C的坐标为(－3，－8)；③当∠BAC＝90°时，则BC2＝AB2＋AC2，即y2＋10y＋34＝50＋4＋y2，解得y＝2，此时点C的坐标为(－3，2)．综上所述，点C的坐标为(－3，－6)或(－3，1)或(－3，－8)或(－3，2)．
1. 确定点的位置：已知线段AB，在平面内找一点P，使△ABP为直角三角形，这样的点P位置有以下三种情况：(1)以A为直角顶点，AB为直角边，点P在过点A与AB垂直的直线上；(2)以B为直角顶点，AB为直角边，点P在过点B与AB垂直的直线上；(3)以点P为直角顶点，AB为斜边，点P在以AB为直径的圆上．
2. 求点P坐标的方法如下：分别表示出点A、B、P的坐标，再根据勾股定理表示出线段AB、BP、AP的长度，由①AB2＝BP2＋AP2，②BP2＝AB2＋AP2，③AP2＝AB2＋BP2列方程解出坐标．
例4 如图，已知抛物线y＝ x2－ x－2与x轴交于A，B两点，与y轴交于点C，连接AC、BC，对称轴为直线l，顶点为M.(1)若点P是y轴上一点，且∠PAC＝90°，求点P的坐标；
【思维教练】当∠PAC＝90°时，易得∠PAO＝∠ACO，根据相等两角的正切值也相等求解即可．
【思维教练】由于点G在x轴上，可知∠COG＝90°，要让它为等腰 直角三角形，则需要分为当点G在x正半轴和负半轴两种情况讨论.
(2)若点G是x轴上一点，当△OCG为等腰直角三角形时，求点G的坐标；
(2)由(1)可知，点C的坐标为(0，－2)．∴OC＝2.∵点G在x轴上，∴当△OCG为等腰直角三角形时，分点G在x轴正半轴和负半轴两种情况讨论：①当点G在x轴正半轴时，∵OC＝OG，∴OG＝2.∴点G的坐标为(2，0)；
②当点G在x轴负半轴时，∵OC＝OG，∴OG＝2.∴点G的坐标为(－2，0)．∴当点G是x轴上一点，△OCG为等腰直角三角形时，点G的坐标为(2，0)或(－2，0)；
(3)若点P是抛物线上一点，是否存在点P，使△PBC是以BC为直角边的直角三角形，若存在，请你求出点P的坐标；若不存在，请说明理由；
【思维教练】因为△PBC是直角三角形，BC为直角边，则分点B、点C为直角顶点两种情况求解即可．
(3)存在，满足条件的点P的坐标为(－5，18)或(－1，0)．设直线BC表达式为y＝kx＋b，将B(4，0)，C(0，－2)代入，得 解得∴直线 BC 的表达式为y＝ x－2，∵BC是Rt△PBC 的直角边，∴分两种情况讨论；①当点 B 是直角顶点时，设 PB 所在直线的表达式为 y＝－2x＋n，将点 B(4，0)代入，解得 n＝8，∴PB 所在直线的表达式为 y＝－2x＋8，
联立 ，即x2＋x－20＝0，解得x＝4(舍去)或 x＝－5，此时点P(－5，18)；②当点 C 是直角顶点时，设 PC 所在直线的表达式为 y＝－2x＋n，将点 C(0，－2)代入，解得 n＝－2，∴PC 所在直线的表达式为 y＝－2x－2，联立 ，即 x2＋x＝0，解得 x＝－1 或 x＝0(舍去)，此时点 P(－1，0)．综上所述，满足条件的点 P 的坐标为(－5，18)或(－1，0)；
(4)若点N是对称轴l上一点，是否存在点N使得△NBC是直角三角形，若存在，请你求出点N的坐标；若不存在，请说明理由．
【思维教练】因为点N是对称轴l上一点，当△NBC是直角三角形时，需分∠NCB，∠NBC，∠BNC为直角三种情况进行讨论，进而求解．
(4)存在，由(1)得抛物线的对称轴 l：x＝－ ，∵点N在对称轴l上，∴设点 N 的坐标为( ，t)，则CN2＝( )2＋(2＋t)2，BN2＝(4－ )2＋t2，BC2＝20，当△NBC是直角三角形时，分以下三种情况：①当∠NCB＝90°时，NC2＋BC2＝NB2，即( )2＋(2＋t)2＋20＝(4－ )2＋t2，解得t＝－5；