安徽省宿州市萧县2023-2024学年八年级上学期期末教学质量检测数学试卷(含解析)

这是一份安徽省宿州市萧县2023-2024学年八年级上学期期末教学质量检测数学试卷(含解析)，共17页。

【本试卷满分150分，考试时间120分钟】
一、选择题（每题4分，共40分）
1．4的算术平方根是（ ）
A．B．C．2D．
2．下列条件中，不能判断是直角三角形的是（ ）
A．B．
C．D．
3．若点在第二象限，且到轴的距离是3，到轴的距离是1，则点的坐标是（ ）
A．B．C．D．
4．，是一次函数图象上的两点，且，则与的大小关系是（ ）
A．B．C．D．无法确定
5．已知一次函数（k为常数，且），无论k取何值，该函数的图像总经过一个定点，则这个定点的坐标是（ ）
A．B．C．D．
6．要得知作业纸上两相交直线AB，CD所夹锐角的大小，发现其交点不在作业纸内，无法直接测量．两同学提供了如下间接测量方案（如图1和图2）：对于方案Ⅰ、Ⅱ，说法正确的是（ ）
A．Ⅰ可行、Ⅱ不可行B．Ⅰ不可行、Ⅱ可行C．Ⅰ、Ⅱ都可行D．Ⅰ、Ⅱ都不可行
7．某排球队6名场上队员的身高（单位：cm）是：180，184，188，190，192，194．现用一名身高为188cm的队员换下场上身高为194cm的队员，与换人前相比，场上队员的身高（）
A．平均数变小，方差变小B．平均数变小，方差变大
C．平均数变大，方差变小D．平均数变大，方差变大
8．《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安.今乙发已先二日，甲仍发长安.问：几何日相逢?译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安.现乙先出发2日，甲才从长安出发.问：多久后甲、乙相逢?设甲出发日，乙出发日后甲、乙相逢，则所列方程组正确的是（ ）
A．B．C．D．
9．如图是一个按某种规律排列的数阵：
根据数阵排列的规律，第n（n是整数，且n≥4）行从左向右数第（n-3）个数是（用含n的代数式表示）（ ）．
A．B．C．D．
10．结合学习函数的经验，小红在平面直角坐标系中画出了函数的图象，如图所示．根据图象，小红得到了该函数四条结论，其中正确的是（ ）
A．y随x的增大而减小B．当时，y有最大值
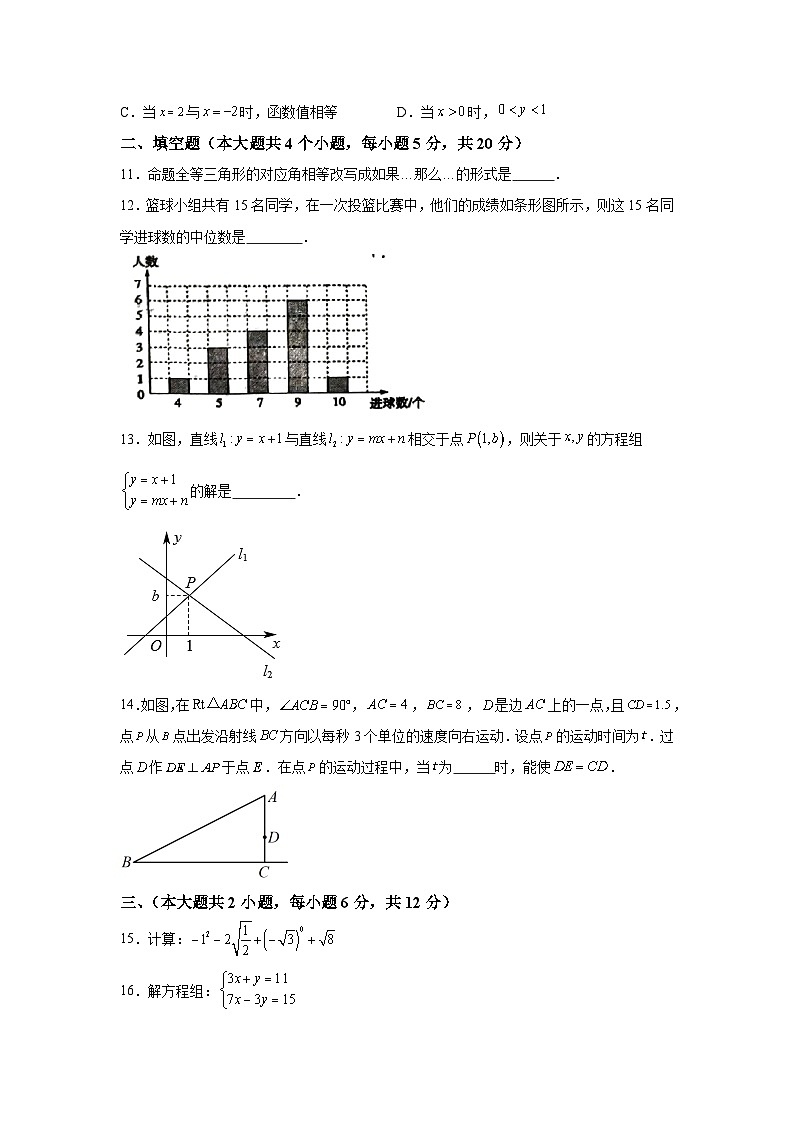
C．当与时，函数值相等D．当时，
二、填空题（本大题共4个小题，每小题5分，共20分）
11．命题全等三角形的对应角相等改写成如果…那么…的形式是 ．
12．篮球小组共有15名同学，在一次投篮比赛中，他们的成绩如条形图所示，则这15名同学进球数的中位数是 ．
13．如图，直线与直线相交于点，则关于的方程组的解是 ．
14．如图，在中，，，，是边上的一点，且，点从点出发沿射线方向以每秒3个单位的速度向右运动．设点的运动时间为．过点作于点．在点的运动过程中，当为 时，能使．
三、（本大题共2小题，每小题6分，共12分）
15．计算：
16．解方程组：
四、（本大题共2小题，每小题9分，共18分）
17．如图是一个平面直角坐标系．
(1)在直角坐标系中画出，其中，，；
(2)画出关于y轴的对称图形（点A，B，C的对应点分别为点，，）；
(3)的三个点横坐标不变，纵坐标分别乘以，再将所得的点，，依次用线段连接起来，得到．直接写出与有怎样的位置关系．
18．两个两位数的和是68，在较大的两位数的右边接着写较小的两位数，得到一个四位数；在较大的两位数的左边写上较小的两位数，也得到一个四位数．已知前一个四位数比后一个四位数大2178，求这两个两位数．
五、（本大题共2小题，每小题10分，共20分）
19．如图，在中，于点D，点E是延长线上的一点，过点E作于点G，交于点F，已知．
(1)求证：平分．
(2)若，求的度数．
20．甲、乙两个商场出售相同的某种商品，每件售价均为3000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一件按原售价收费，其余每件优惠30%；乙商场的优惠条件是：每件优惠25%．设所买商品为x件时，甲商场收费为y1元，乙商场收费为y2元．
（1）分别求出y1，y2与x之间的关系式；
（2）当甲、乙两个商场的收费相同时，所买商品为多少件？
（3）当所买商品为5件时，应选择哪个商场更优惠？请说明理由．
六、（本题满分12分）
21．为贯彻《关于全面加强新时代大中小学劳动教育的意见》，各学校都在深入开展劳动教育．某校为了解七、八年级学生一学期参加课外劳动时间（单位：小时）的情况，从该校七、八年级中各随机抽查了20名学生进行问卷调查，并将调查结果进行整理，描述和分析（，，，，），下面给出了部分信息．
七年级抽取的学生在C组的课外劳动时间为：40，40，50，55
八年级抽取的20名学生的课外劳动时间为：10，15，20，25，30，35，40，40，45，50，50，50，55，60，60，75，75，80，90，95
七年级抽取的学生的课外劳动时间的扇形统计图
七、八年级抽取的学生的课外劳动时间的统计量
根据以上信息，解答下列问题：
（1）直接写出，，的值；
（2）根据以上数据，在该校七、八年级中，你认为哪个年级参加课外劳动的情况较好？请说明理由（一条理由即可）；
（3）若该校七、八年级分别有学生400人，试估计该校七、八年级学生一学期课外劳动时间不少于60小时的人数之和．
七、（本题满分14分）
22．如图（1），平分，．
(1)试说明与的位置关系，并予以证明；
(2)如图（2），当时，点E，F分别在和的延长线上运动，试探讨和的数量关系；
(3)如图（3），和的延长线交于点G，过点D作交于点H，若，问当为多少度时，．
八、（本题满分14分）
23．如图，已知函数的图象与轴交于点，一次函数的图象经过点，与轴以及的图象分别交于点、，且点的横坐标为1．
(1)点的坐标是______直线的解析式是_______
(2)连接，求的面积．
(3)点是直线上一点（不与点重合），设点的横坐标为，的面积为，请直接写出与之间的关系式．

参考答案与解析
1．C
解析：解：∵，
∴4的算术平方根是2．
故选：C
2．D
解析：解：A.∵，
∴可设 ，
∴，
∴是直角三角形，故此选项不符合题意；
B.∵，
∴可设，
∴ ，
∴是直角三角形，故此选项不符合题意；
C.∵，
∴，
∵，
∴，
∴是直角三角形，故此选项不符合题意；
D.∵，，
∴，
∴不是直角三角形，故此选项符合题意；
故选：D．
3．B
解析：解：∵点P到轴的距离是3，到轴的距离是1，
∴点P的横坐标的绝对值为1，纵坐标的绝对值为3，
又∵点在第二象限，
∴点P的坐标为，
故选B．
4．A
解析：解：∵一次函数解析式为，，
∴y随x的增大而增大，
又∵，
∴．
故选：A．
5．B
解析：解：∵，
当时，，
∴无论k取何值，该函数的图像总经过一个定点；
故选：B．
6．C
解析：方案Ⅰ：如下图，即为所要测量的角
∵
∴
∴
故方案Ⅰ可行
方案Ⅱ：如下图，即为所要测量的角
在中：
则：
故方案Ⅱ可行
故选：C
7．A
解析：解：原数据的平均数为，
则原数据的方差为×[（180-188）2+（184-188）2+（188-188）2+（190-188）2+（192-188）2+（194-188）2]= ，
新数据的平均数为，
则新数据的方差为×[（180-187）2+（184-187）2+（188-187）2+（190-187）2+（188-187）2+（192-187）2]= ，
所以平均数变小，方差变小，
故选：A．
8．D
解析：解：由题可知，甲的效率为，乙的效率为，
设甲出发日，乙出发日后甲、乙相逢，根据题意列方程组：
．
故选：D．
9．C
解析：由图中规律知，前（n-1）行的数据个数为2+4+6+…+2（n-1）＝n（n-1），
∴第n（n是整数，且n≥4）行从左向右数第（n-3）个数的被开方数是：n（n-1）+n-3＝n2-3，
∴第n（n是整数，且n≥4）行从左向右数第（n-3）个数是：
故选：C．
10．D
解析：A：由图象可知，当时，随的增大而增大，故本选项不合题意；
B：函数的自变量的取值范围为，故本选项不合题意；
C：当时，函数值为；当时，函数值为1，故本选项不合题意；
D：由图象可知，当时，，故本选项符合题意．
故选：D．
11．如果两个三角形是全等三角形，那么它们的对应角相等．
解析：∵原命题的条件是：两个三角形是全等三角形，结论是：对应角相等，
∴命题“全等三角形的对应角相等”改写成“如果…，那么…”的形式是如果两个三角形是全等三角形，那么它们的对应角相等．
故答案为：如果两个三角形是全等三角形，那么它们的对应角相等．
12．7
解析：解：将这组数据从小到大的顺序排列后，处于中间位置的数是7个，
那么由中位数的定义可知，这组数据的中位数是7个．
故答案为：7．
13．
解析：解：∵直线经过点，
∴，
解得，
∴，
∴关于x，y的方程组的解为：，
故答案为：．
14．或
解析：解：①点在线段上时，过点作于，如图1所示：
则，
，
平分，
，
又，
（AAS）,
，，
，
，
，
，
，
在中，由勾股定理得：，
解得：；
②点在线段的延长线上时，过点作于，如图2所示：
同①得：(AAS)，
，，
，
，
，
，
，
，
在中，由勾股定理得：，
解得：．
综上所述，在点的运动过程中，当的值为或时，能使．
故答案为：或 ．
15．
解析：原式
16．
解析：，
由①得：y＝11﹣3x③，将③代入②得：7x﹣3（11﹣3x）＝15，解得：x＝3，将x＝3代入③得：y＝11﹣3×3＝2，
∴原方程组的解为：.
17．(1)见解析
(2)见解析
(3)与关于x轴对称
解析：（1）解：如图所示，即为所求．
（2）解：如图所示，即为所求．
（3）解：如图所示，即为所求，与关于x轴对称．
18．这两个数是45和23．
解析：设较大的两位数为x，较小的两位数为y，
根据题意，得
，
解得．
答：这两个数是45和23．
19．(1)见解析
(2)
解析：（1）证明：，，
，
，
，．
，
，
平分．
（2），
．
，
．
，
，
．
20．（1）；y2=2250x；
（2）甲、乙两个商场的收费相同时，所买商品为6件；
（3）所买商品为5件时，应选择乙商场更优惠．
解析：（1）当x=1时，y1=3000；
当x＞1时，y1=3000+3000（x﹣1）×（1﹣30%）=2100x+900．
∴；
y2=3000x（1﹣25%）=2250x，
∴y2=2250x；
（2）当甲、乙两个商场的收费相同时，2100x+900=2250x，
解得x=6，
答：甲、乙两个商场的收费相同时，所买商品为6件；
（3）x=5时，y1=2100x+900=2100×5+900=11400，
y2=2250x=2250×5=11250，
∵11400＞11250，
∴所买商品为5件时，应选择乙商场更优惠．
21．（1），，；（2）八年级，见解析；（3）300人
解析：.解：（1）七年级B组所占百分比为：1-10%-20%-25%-15=30%，m=30，
根据扇形统计图可知，七年级A组有2人，B组有6人，C组有4人，D组有5人，E组有4人，中位数是第10个和第11个数据的平均数，第10个数据是40，第11个数据是50，则中位数是（40+50）÷2=45，a=45，
八年级数据中，50出现了3次，最多，所以，b=50，
故答案为，，；
（2）八年级学生参加课外劳动的情况较好，理由如下：
因为七、八年级被抽取的学生的课外劳动时间的平均数都是50，而八年级的中位数50高于七年级的中位数45，所以八年级学生参加课外劳动的情况较好；（用数据说明，合理即可）
（3）（人）
答：估计该校七、八年级学生一学期课外劳动时间不少于60小时的人数之和为300人．
22．(1)，见解析
(2)
(3)当为时，
解析：（1）．
证明：平分，
，
，
，
∴．
（2）当时，．
点E，F分别在和的延长线上运动，
是的外角，
．
（3）∵，，
，
，
∴是等腰三角形，
，
当时，
故当为时，．
23．(1)；
(2)
(3)
解析：（1）将代入函数得D点纵坐标为2，将点，代入得：，解得，
故解析式为：
故答案为： ；；
（2）
如图：点A的坐标为，，点C的坐标为，
∴
；
（3）①如图，点P在之间：
；
②点P在B点下方,如图：
；
③点P在D点的上面
；
综上所述：年级
平均数
众数
中位数
方差
七年级
50
35
580
八年级
50
50
560