
所属成套资源:2024年五升六数学暑假专题训练(人教版)
2024年五升六数学暑假专题训练 专题01-观察物体(三)(人教版)
展开
这是一份2024年五升六数学暑假专题训练 专题01-观察物体(三)(人教版),共13页。试卷主要包含了如图,搭一搭,填一填等内容,欢迎下载使用。
能力巩固提升
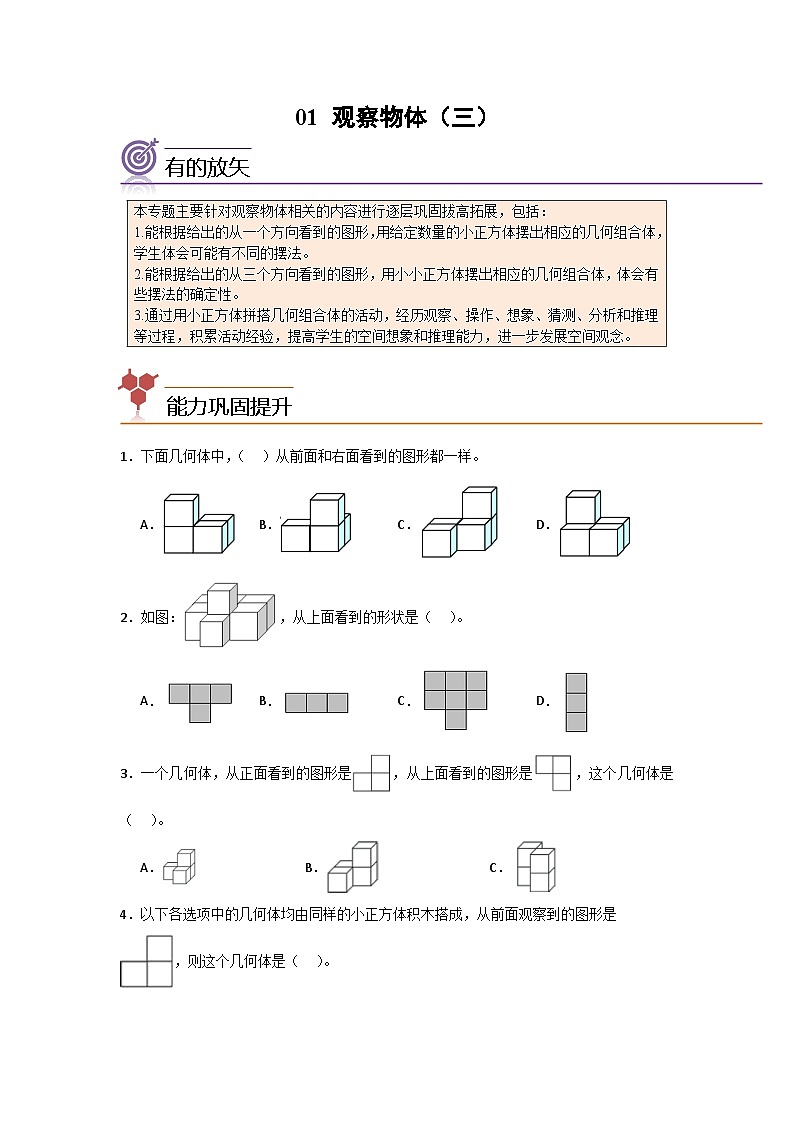
1.下面几何体中,( )从前面和右面看到的图形都一样。
A.B.C.D.
2.如图:,从上面看到的形状是( )。
A.B.C.D.
3.一个几何体,从正面看到的图形是,从上面看到的图形是,这个几何体是( )。
A.B.C.
4.以下各选项中的几何体均由同样的小正方体积木搭成,从前面观察到的图形是,则这个几何体是( )。
A.B.C.D.
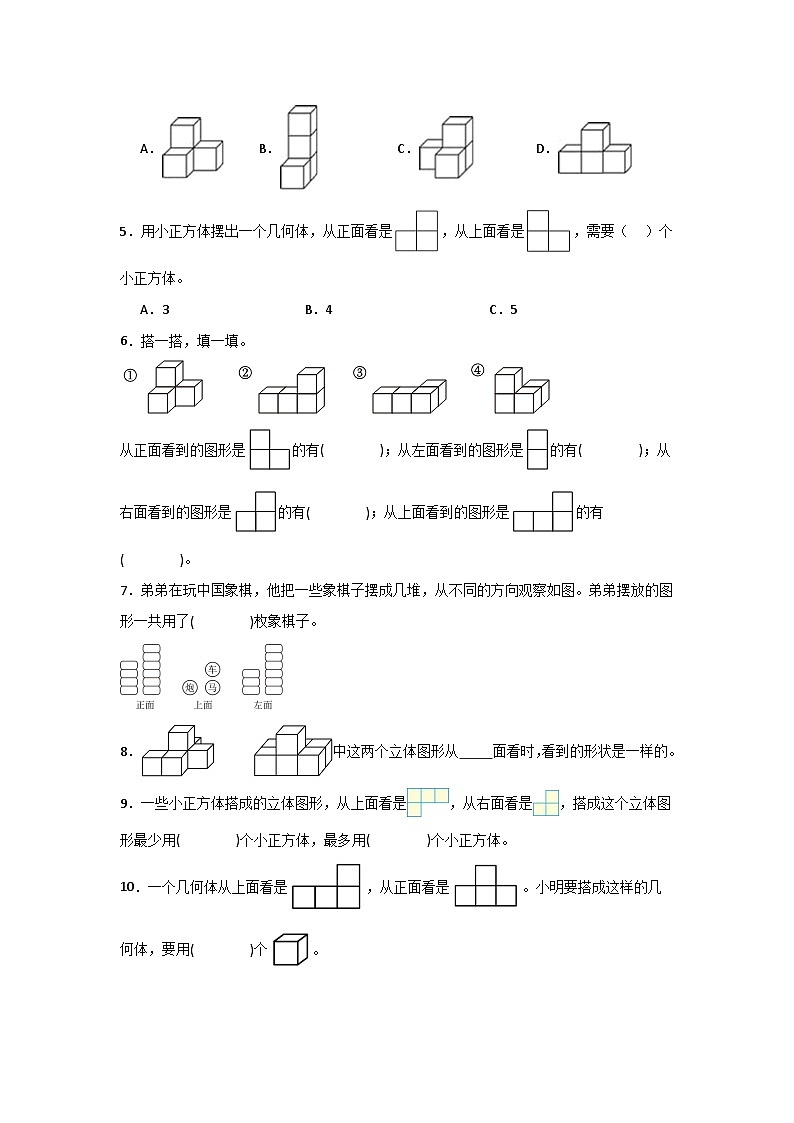
5.用小正方体摆出一个几何体,从正面看是,从上面看是,需要( )个小正方体。
A.3B.4C.5
6.搭一搭,填一填。
从正面看到的图形是的有( );从左面看到的图形是的有( );从右面看到的图形是的有( );从上面看到的图形是的有( )。
7.弟弟在玩中国象棋,他把一些象棋子摆成几堆,从不同的方向观察如图。弟弟摆放的图形一共用了( )枚象棋子。
8.中这两个立体图形从 面看时,看到的形状是一样的。
9.一些小正方体搭成的立体图形,从上面看是,从右面看是,搭成这个立体图形最少用( )个小正方体,最多用( )个小正方体。
10.一个几何体从上面看是,从正面看是。小明要搭成这样的几何体,要用( )个。本专题主要针对观察物体相关的内容进行逐层巩固拔高拓展,包括:
1.能根据给出的从一个方向看到的图形,用给定数量的小正方体摆出相应的几何组合体,学生体会可能有不同的摆法。
2.能根据给出的从三个方向看到的图形,用小小正方体摆出相应的几何组合体,体会有些摆法的确定性。
3.通过用小正方体拼搭几何组合体的活动,经历观察、操作、想象、猜测、分析和推理等过程,积累活动经验,提高学生的空间想象和推理能力,进一步发展空间观念。
综合拔高拓展
1.小丽用5个同样的小正方体摆几何体,从上面看是,从左面看是。一共有( )种不同的摆法。
A.3B.2C.1
2.亮亮搭的积木从上面看是(正方形上面的数表示在这个位置上所用的小正方体的个数),从左面看是( )。
A.B.C.D.
3.要想使下图左面和上面看到的图形不变,最多能增加( )个小正方体。
A.1B.2C.3D.4
4.用5个同样的小正方体摆成从前面看是的几何体(摆时,接触的两个面要完全重合),有( )种摆法。
A.3B.4C.6D.8
5.改变图中涂色小正方体的位置,且使任意两个小正方体的面都有相邻,使几何体从左面看到的图形不变,有( )个不同的位置可以选择。
A.3B.4C.5
6.一个用积木搭成的几何体,从上面看是,积木上面的数字表示在这个位置上所用的小正方体的个数。搭这组积木,从正面看是( ),从左面看是( )。
7.用同样的小正方体搭成一个几何体,从上面和左面看到的形状如图所示,搭这个几何体至少需要( )个小正方体。
从上面看 从左面看
8.仔细观察下图:从左面看,明明搭的积木中( )号的形状和聪聪搭的是相同的。明明搭的积木中,从正面看,形状相同的是( )号和( )号。
9.下面是用小正方体搭建的一些几何体。
(1)从正面看到的是的有( ),从侧面看到的是的有( ),从上面看到的是的有( )。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,有多少种不同的摆法?
10.(1)如下图立体图形由( )个小正方体拼成。
(2)画出的图形是从( )面看到的。
(3)从正面和上面看到的图形是什么样的?画一画吧!
11.冬冬用同样的小正方体搭了一个图形,从正面、左面和上面看到的图形分别如图。
(1)从右面看是什么图形,你能画出来吗?请在方格纸上画一画。
(2)想一想,搭这个图形需要 个小正方体。
参考答案
能力巩固提升
1.A
【分析】结合组合体自身的特点,以及三视图规律,先确定看到的图形有几层,每层的的小正方形有几列,根据题意,通过正视图、右视图来确定所看到图形的样子。
【详解】A.仔细观察后,从前面看2层3个正方形,从右面看有2层3个正方形。
B.仔细观察后, 从前面看是2层3个正方形,从右面看有2层3个正方形,方向相反。
C.仔细观察后, 从前面看有2层3个正方形,从右面看是2层4个正方形。
D.仔细观察后, 从前面看有2层3个正方形,从右面看是2层3个正方形,方向相反。
2.C
【分析】从上面观察几何体,可以看到有3行7个小正方形,前一行有1个且居中,后面两行各有3个,据此得出从上面看到的形状。
【详解】
,从上面看到的形状是。
3.A
【分析】根据题意,我们可以把每一个选项的从正面看到的图形和从上面看的图形画出来,进行比较分析。
【详解】
A. ,从正面看到的图形是,从上面看到的图形是,符合题意;
B. ,从正面看到的图形是,从上面看到的图形是,不符合题意;
C. ,从正面看到的图形是,从上面看到的图形是,不符合题意。
4.C
【分析】A.从前面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
B.从前面看有1列3个小正方形;
C.从前面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;
D.从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形。
【详解】
A.从前面观察到的图形是;
B.从前面观察到的图形是;
C.从前面观察到的图形是;
D.从前面观察到的图形是。
这个几何体是。
5.B
【分析】通过观察可知,这个几何体有2层,从上面看到的图形可知,下层一共有3个小正方体,2个在前排,1个在后排,靠左边;从正面可知,上层只有1个,在前排的右边,所以一共有(1+3)个小正方体。
【详解】1+3=4(个)
根据分析可知,需要4个小正方体。
6. ①④ ② ① ③
【分析】
从正面看到的图形是,说明从正面能看到两层3个小正方形,下层2个,上层1个且居左;
从左面看到的图形是,说明从左面能看到两层并列放的2个小正方形;
从右面看到的图形是,说明从右面能看到两层3个小正方形,下层2个,上层1个且居右;
从上面看到的图形是,说明从上面能看到两层4个小正方形,下层3个,上层1个且居右;
据此找出符合要求的几何体。
【详解】如图:
从正面看到的图形是的有①④;从左面看到的图形是的有②;从右面看到的图形是的有①;从上面看到的图形是的有③。
7.13
【分析】根据从上面、正面和左面观察到的形状可知,有3列,前面2列,左面4枚,右面6枚,后面一列3枚。求和即可。
【详解】4+3+6
=7+6
=13(枚)
弟弟摆放的图形一共用了13枚象棋子。
8.正
【分析】
观察图形从正面看到的图形都是;从左面看到的图形分别是、;从右面看到的图形分别是、;从上面看到的图形分别是、;据此解答即可。
【详解】由分析可知:
中这两个立体图形从正面看时,看到的形状是一样的
9. 5 7
【分析】先根据从上面看到的平面图形确定小正方体的位置,再根据从右面看到的平面图形确定每列小正方体的最高层数,最后各位置上的小正方体数量相加求和,据此解答。
【详解】从上面看是,则各位置上至少有1个小正方体,从右面看是,左边一列小正方体只有一层,右边一列至少有一个小正方体的最高层数为2层,所需小正方体最少时(摆法不唯一),2+1+1+1=5(个),所需小正方体最多时,2+2+2+1=7(个)。
10.5
【分析】从上面看是,说明这个几何体的最下层是;从正面看是,所以这个几何是。即这个几何体有两层,上层有1个小正方体,下层有4个小正方体。
【详解】1+4=5(个)
所以小明要搭成这样的几何体,要用5个。
综合拔高拓展
1.A
【分析】从上面、左面看到的形状,可知这个几何体是2层2行,下层有4个小正方体,前一行有3个,后一行有1个且居中;上层有1个小正方体,可以摆放在前一行3个小正方体的上方,因此有3种不同的摆法。
【详解】结合从上面、左面看到的平面图,可以得出下面的几何体:
一共有3种不同的摆法。
2.B
【分析】根据从上面看到的图形以及各个小正方形上的数字可知,这个立体图形从前往后分成两行,第一行最高有3个小正方体,第二行最高也有3个小正方体,那么从左面看时,能看到三层小正方形,每层两个小正方形。
【详解】
从左面看是。
3.B
【分析】观察图形可知,从左面看有2层,上层1个小正方形,下层1个小正方形;从上面看,有1层共3个小正方形;要想左面和上面看到的图形不变,最多在此图形的上层左侧并排加上2个小正方体,据此解答。
【详解】要想使下图左面和上面看到的图形不变,最多能增加2个小正方体。
4.D
【分析】
用5个同样的小正方体摆成从前面看是的几何体,需要添加2个小正方体,使从正面看到的图形不变,则这2个小正方体可以放在下层的2个小正方体的任意一个的前面一行或者后面一行,一共有8种不同的摆法。
【详解】
用5个同样的小正方体摆成从前面看是的几何体(摆时,接触的两个面要完全重合),有8种摆法。
5.C
【分析】
通过对图的观察,该图形从左边看见的图形为:,涂色小正方体可以往左一格或往右一格,也可以放到三个连着的小正方体中任意一个的后面,据此解答。
【详解】该小正方体移动情况如下:
总共有5种情况,从左看见的图形依然为。
故答案为:C
6. ② ①
【分析】根据从上面看到的图形可以得出:从正面看有3层,底层有4个小正方体,第二层靠左有3个小正方体,顶层靠左有1个小正方体;从左面看,共有3层,底层有2个小正方体,第二层对齐底层有2个小正方体,顶层靠左有1个小正方形,据此得出从正面、左面看到的图形。
【详解】由分析可知,搭这组积木,从正面看是,即图形②;从左面看是,即图形①。
7.5
【分析】根据从上面看到的图形可知,这个几何体有2层4个小正方体,前面有3个小正方体,后面1个小正方体;
从左面看2层,3个小正方体,上层1个小正方体,下层2个小正方体;由此可知,下层一共需要4个小正方体,上层最少需要1个小正方体,据此解答。
【详解】4+1=5(个)
用同样的小正方体搭成一个几何体,从上面和左面看到的形状如图所示,搭这个几何体至少需要5个小正方体。
8. ①② ② ③
【分析】聪聪搭的积木从左面看有2层,上层1个小正方形,下层2个小正方形,左齐;
明明搭的积木①:从左面看有2层,上层1个小正方形,下层2个小正方形,左齐;
②:从左面看有2层,上层1个小正方形,下层2个小正方形,左齐;
③:从左面看有2层,上层1个小正方形,下层2个小正方形,右齐;
由此可知,明明搭的积木的①和②与聪聪搭的积木从左面看相同;
明明搭的积木从正面看①:有2层,上层1个小正方形,下层3个小正方形,左齐;
②:有2层,上层1个小正方形,下层3个小正方形,居中;
③:有2层,上层1个小正方形,下层3个小正方形,居中;由此可知,明明搭的积木的②和③从正面看相同,据此解答。
【详解】根据分析可知,仔细观察下图:从左面看,明明搭的积木中①②号的形状和聪聪搭的是相同的。明明搭的积木中,从正面看,形状相同的是②号和③号。
9.(1)④⑤;①③;④
(2)5
【分析】(1)从正面看到的是二行,最下面一行三个小正方形并排,上面一行一个放在中间;从侧面看是一列两个,上下排列;从上面看是二行三列,上下行各两个正方形,呈“Z”型排列。由此分析判断。
(2)几何体⑥从正面看到的形状如右: ,根据此图,展开想象,确定物体的形状。
【详解】
(1)从正面看到的是的有(④⑤),从侧面看到的是的有(①③),从上面看到的是的有(④)。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,可以有如下摆法。
共有5种。
10.(1)8
(2)右
(3)见详解
【分析】
(1)观察立体图形,分两层,上层有1个小正方体,下层有7个小正方体,据此得解。
(2)观察平面图形,分两层共4个小正方形,下层3个,上层1个且居右,据此确定是从右面观察立体图形得到的这个平面图形。
(3)从正面能看到4个小正方形,分两层,上层1个且居中,下层3个;从上面能看到7个小正方形,分三层,上层、中层各3个,下层1个且居右;据此画出从正面和上面看到的图形。
【详解】
(1)1+7=8(个)
立体图形由8个小正方体拼成。
(2)画出的图形是从右面看到的。
(3)如图:
11.(1)见详解;
(2)7
【分析】观察图形可知:从正面看到的图形有3层,下面一层是3个正方形,第二列1个正方形居中一层,第三列1个正方形居中一层,从左面看到的图形是有3层,下面一层、中间层是2个正方形,上面一层是1个正方形,靠左边;从上面看到的图形有2列2层,在第一层,中间一列是1个正方形,在第二层,是3个正方形,从右面看到的图形是有3层,下面一层、中间层是2个正方形,上面一层是1个正方形,靠右边;由此可知一共7个正方体。
【详解】(1)
(2)搭这个图形需要7个小正方体。
相关试卷
这是一份2024年四升五数学暑假专题训练 专题4 观察物体(北师大版),文件包含2024年四升五数学暑假专题训练专题4观察物体教师版北师大版docx、2024年四升五数学暑假专题训练专题4观察物体学生版北师大版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
这是一份2024年四升五数学暑假专题训练 专题02:观察物体(二)(人教版),共12页。
这是一份2024年五升六数学暑假专题训练 专题05:图形的运动(三)(人教版),共10页。试卷主要包含了选择题等内容,欢迎下载使用。









