






数学选择性必修第二册8.2离散型随机变量及其分布列优秀课件ppt
展开投掷一枚硬币,设正面向上的概率为p,连续投掷3次,则3次都出现正面向上的概率为多少?
分析:设Ai=”第i次正面朝上“(i=0,1,2,3) B3=”3次都正面朝上”,则B3=A1A2A3. 连续投掷3次硬币,每次结果相互独立,因此事件A1,A2,A3相互独立. 则P(B3)=P(A1A2A3)=P(A1)P(A2)P(A3).
投掷一枚硬币,设正面向上的概率为p,连续投掷3次,则只出现1次正面向上的概率为多少?
投掷一枚硬币,设正面向上的概率为p,连续投掷3次,出现k(k=0,1,2,3)次正面向上的概率为多少?
把只包含两个可能结果的试验叫做伯努利试验.
n重伯努利试验的特征:
将一次伯努利试验独立的重复进行n次所组成的随机试验称为n重伯努利试验.
1、同一个伯努利试验重复做n次;
2、各次试验的结果相互独立.
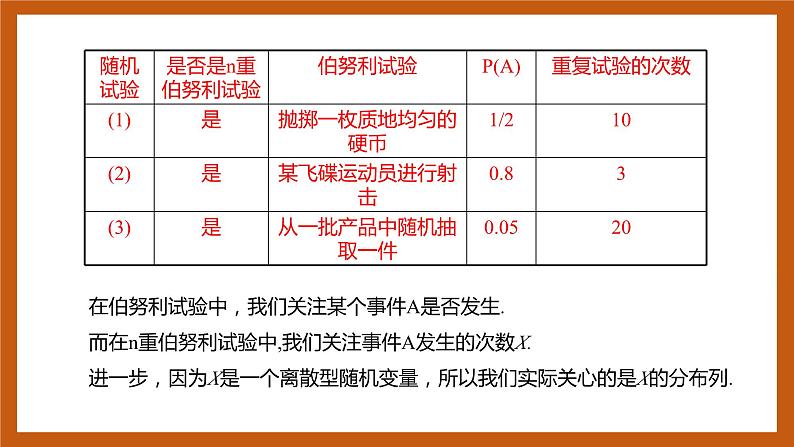
思考:下面3个随机试验是否为n重伯努利试验?如果是,那么其中的伯努利试验是什么?对于每个试验,定义“成功”的事件为A,那么A的概率是多大?重复试验的次数是多少?
(1)抛掷一枚质地均匀的硬币10次.(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.(3)一批产品的次品率为5%,有放回地随机抽取20件.
在伯努利试验中,我们关注某个事件A是否发生.而在n重伯努利试验中,我们关注事件A发生的次数X.进一步,因为X是一个离散型随机变量,所以我们实际关心的是X的分布列.
探究:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
用Ai表示“第i次射击中靶”(i=1,2,3),用如下图的树状图表示试验的可能结果:
试验结果 X的值
由分步乘法计数原理,3次独立重复试验共有23=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积,由概率的加法公式和乘法公式得:
中靶次数X的分布列为:
思考:如果连续射击4次,类比上面的分析,表示中靶次数X等于2的结果有哪些?写出中靶次数X的分布列.
表示中靶次数X等于2的结果
如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布,记作X~B(n,p)
1、在一次试验中,事件A发生与不发生二者必居其一2、事件A在每次的试验中发生的概率相同3、试验重复的进行了n(n≥2)次,且每次试验结果相互独立,互不影响
例1:将一枚质地均匀的硬币重复抛掷10次,求:(1)恰好出现5次正面朝上的概率。(2)正面朝上出现的频率在[0.4,0.6]内的概率。
确定二项分布模型的步骤:
1、明确伯努利试验及事件A的意义,确定事件A发生的概率p;2、明确重复试验的次数n,并判断各次试验的独立性;3、设X为n次独立重复试验中事件A发生的次数,则X~B(n,p)
思考:假设随机变量X服从二项分布X~B(n,p),则X的均值和方差各是什么?
(1)当n=1时,X服从两点分布,分布列为:P(X=0)=1-p,P(X=1)=p均值和方差分别为E(X)=p,D(X)=p(1-p)(2)当n=2时,X的分布列为:P(X=0)=(1-p)2,P(X=1)=2p(1-p),P(X=2)=p2,均值和方差分别为:E(X)=0 x (1-p)2+1 x 2p(1-p)+2 x p2=2pD(X)=02 x (1-p)2+12 x 2p(1-p)+22 x p2 - (2p)2=2p(1-p)
一般地,如果X~B(n,p),那么E(X)=np,D(X)=np(1-p)
苏教版 (2019)选择性必修第二册8.1条件概率优质课件ppt: 这是一份苏教版 (2019)选择性必修第二册<a href="/sx/tb_c4009178_t3/?tag_id=26" target="_blank">8.1条件概率优质课件ppt</a>,共39页。PPT课件主要包含了导入课题,新知探究,条件概率,设PA0则,条件概率的性质,全概率公式,PR2R1,PB2R1,PR2B1,PB2B1等内容,欢迎下载使用。
高中数学苏教版 (2019)选择性必修第二册7.3组合优质课件ppt: 这是一份高中数学苏教版 (2019)选择性必修第二册<a href="/sx/tb_c4009174_t3/?tag_id=26" target="_blank">7.3组合优质课件ppt</a>,共1页。
高中数学苏教版 (2019)选择性必修第二册7.2排列完美版课件ppt: 这是一份高中数学苏教版 (2019)选择性必修第二册<a href="/sx/tb_c4009173_t3/?tag_id=26" target="_blank">7.2排列完美版课件ppt</a>,共1页。













