

2024年四升五数学暑假专题训练 专题07:图形的运动(二)(人教版)
展开能力巩固提升
1.将一张长方形纸按下边的方法对折两次,然后剪去一个角,展开后得到的图形是( )。
A. B. C. D.
2.甲骨文是我国的一种古老文字,是迄今为止我国发现的年代最早的成熟文字系统。下列甲骨文中,( )不是轴对称图形。
A.B.C.D.
3.下面图形中,( )一定是轴对称图形。
A.等腰三角形B.锐角三角形C.直角三角形D.钝角三角形
4.图中的圆从A( )可以到B。
A.向右平移3格B.向右平移4格C.向左平移4格D.向左平移3格
5.平移后的图形和原图形相比,( )。
A.大小、形状和位置都变了B.大小、形状和位置都不变
C.大小、形状不变,位置变了D.位置不变,大小和形状变了
6.图中阴影部分的周长是( )cm。
A.46B.38C.23D.44
7.下面图形中,只有一条对称轴的是( ),有无数条对称轴的是( )(填序号)。
①;②;③;④。
8.涂色部分占整个图形的几分之几?
综合拔高拓展
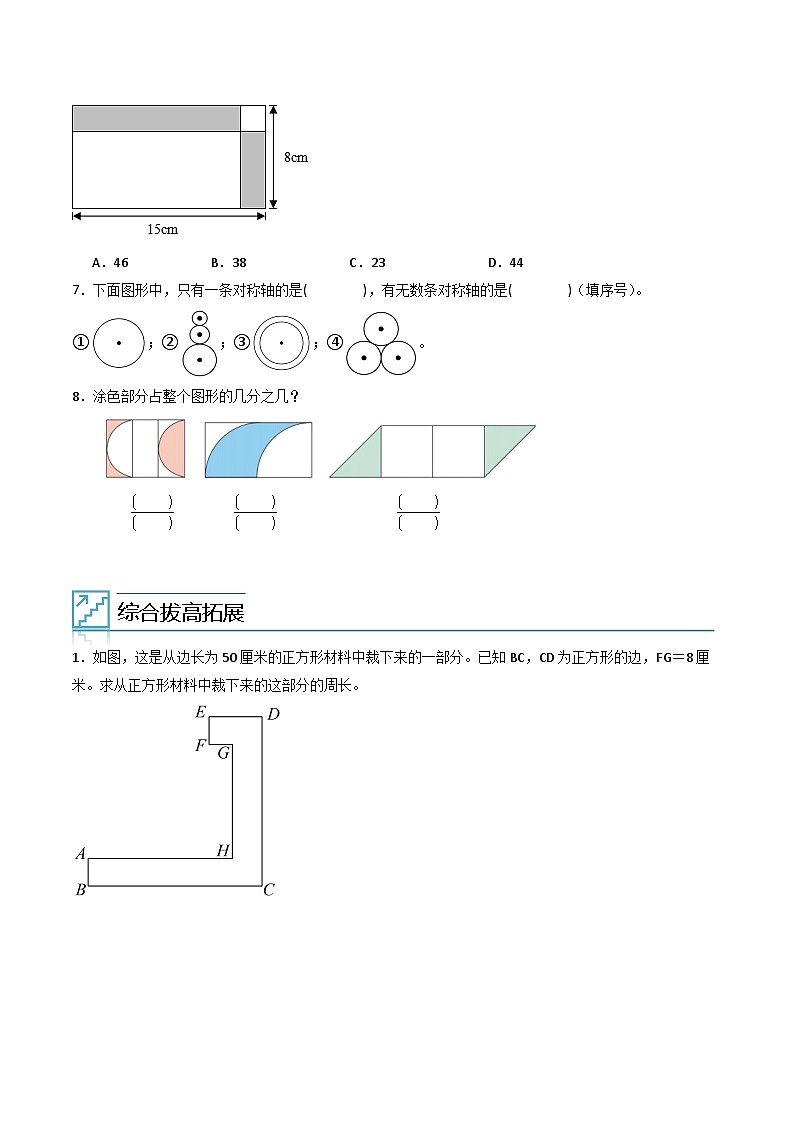
1.如图,这是从边长为50厘米的正方形材料中裁下来的一部分。已知BC,CD为正方形的边,FG=8厘米。求从正方形材料中裁下来的这部分的周长。
2.巧算这块菜地的面积有多少平方米?
3.如下图,网格图上(每一小格的边长是1厘米)有4张同样大小的正方形彩纸(部分重叠),重叠部分的边长是正方形边长的一半。求重叠后整个图形的周长。
4.如图1所示,公园内有一块长22米,宽14米的长方形空地。在空地上铺设一条宽2米的曲折石子小路,其余地方都铺上草坪。你能算出草坪的面积吗?可以先在图2中画一画,再把你的想法写下来。
5.下面的两种平移结果一样吗?描述一样吗?
9.按要求画一画:
(1)图①向( )平移了( )格;
(2)画出图③的另一半,使它成为一个轴对称图形;
(3)图②是一个图形向左平移5格后得到的,请你画出这个图形原来的位置。
7.下图是李明家和图书馆所在位置的平面图。李明沿着图中的实线道路,从家步行到图书馆。他前3分钟走了252米,照这样的速度,李明还要走多少分钟才能到达图书馆?
8.
(1)画出图中三角形ABO(图1)指定底边上的高。
(2)把上图中的图2先向( )平移( )格,再向( )平移( )格后能与图3拼成一个长方形,这个长方形的面积是( )平方厘米。
(3)先补全上图中图4这个轴对称图形,然后画出这个图形向右平移6格后的图形。
9.农民叔叔阿根想用20m长的金属网建一个靠墙的长方形鸡舍(如图).要使所建的鸡舍面积最大,BC的长应是多少米?
10.星期六,爸爸给红红一张试卷,让她自己做测试并记录时间,开始做时红红从镜子里看了一下时钟,做完试卷时她又从镜子里看了一下时钟,红红用了多长时间?
参考答案
能力巩固提升
1.B
【分析】将一个长方形对折两次,对折后的图形以折痕为对称图形,剪去的角只剪在了第二次对折的折痕处,并没有剪在第一次的折痕处,所以会关于第一次对折的折痕对称,再判断选项即可。
【详解】第一次折痕是竖折痕,第二次折痕是横折痕,剪去一个角,只会剪在横折痕处,并且是关于竖折痕的左右对称图形,综合判断展开后得到的图形是 。
故答案为:B
2.C
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】
A. 是轴对称图形;
B. 是轴对称图形;
C. 不是轴对称图形;
D. 是轴对称图形。
故答案为:C
3.A
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】A.等腰三角形是轴对称图形;
B.锐角三角形不一定是轴对称图形,两条边相等或者三条边相等时,这个三角形才是轴对称图形;
C.直角三角形不一定是轴对称图形,两条直角边相等时这个三角形才是轴对称图形;
D.钝角三角形不一定是轴对称图形,两条边相等时这个三角形才是轴对称图形;
故答案为:A
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
4.B
【分析】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。根据平移的特征以及停的相对位置可以确定圆形是从A向右平移4格到B,据此解答即可。
【详解】根据上述分析可得:图中的圆从A向右平移4格可以到B。
故答案为:B
5.C
【分析】平移是在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
【详解】根据分析可知平移后的图形和原图形相比,大小、形状不变,位置变了。如图:
故答案为:C
6.A
【分析】图中阴影部分图形为两个长方形,通过平移可以发现,两个长方形的周长为就是大长方形的周长,再根据长方形周长=(长+宽)×2算式周长即可。
【详解】可以把原图的长方形内侧的边平移,会发现阴影部分的周长就是大长方形的周长,如图:
(15+8)×2
=23×2
=46cm
故答案为:A
【点睛】此题考查长方形周长的灵活运用。
7. ② ①③
【分析】轴对称图形定义为平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,这个图形是轴对称图形,这条直线叫做对称轴。
【详解】
①有无数条对称轴;②只有一条对称轴;③有无数条对称轴;④有三条对称轴。
只有一条对称轴的是②,有无数条对称轴的是①,③。
8.;;
【分析】把一个图形平均分成几份,每份占这个整体的几分之一;
题中图形涂色部分不规则,我们可以根据平移不改变图形的大小和方向、只改变图形的位置的这一特性,将涂色部分进行平移拼组,即可知道涂色部分占整体的几分之几。据此解答。
【详解】
由图可知,第一幅图涂色部分占整体的,第二福图涂色部分占整体的,第三幅图涂色部分占整体的。
综合拔高拓展
1.216厘米
【分析】这个图形为不规则图形,需要通过平移的方式将小段的线段组合成已知的线段。然后再利用周长的定义求解。
【详解】如图,这个图形竖着的小段线段有AB、GH和EF,将它们移动到右边,可组成一条和线段CD一样长的线段,也就是50厘米长。
同理,这个图形横着的小段线段有AH、ED和FG,如果直接平移会比线段BC长。所以在线段上取点I,使得EI=FG。将小段线段AH、ID平移,可组成一条和线段BC一样长的线段,也就是50厘米长。同时,还剩下线段EI和线段FG,它们都是8厘米长。
故通过平移,可将不规则图形的周长转化为4条长为50厘米的线段和2条长为8厘米的线段。
50×4=200(厘米)
8×2=16(厘米)
200+16=216(厘米)
答:这部分的周长是216厘米。
【点睛】通过平移将未知的小段线段转化为已知的线段是解决本题的关键。
2.336平方米
【分析】如下图,把路平移到右边,西红柿菜地平移到与黄瓜菜地连在一起,求菜地的面积就等于求长为(30-2)米,宽为12米的长方形的面积,长方形的面积=长×宽,把数据代入计算即可解答。
【详解】(30-2)×12
=28×12
=336(平方米)
答:这块菜地的面积有336平方米。
3.20厘米
【分析】由图可知,重叠后整个图形为不规则图形。直接求它的周长比较困难,我们可通过平移将其转化为规则图形,然后再利用规则图形的周长公式求解。
【详解】如下图,把横着的小段线段和竖着的小段线段平移,可将原来不规则的图形转化为边长为5厘米的正方形。
整个图形的周长:5×4=20(厘米)
答:重叠后整个图形的周长是20厘米。
4.画图见详解;240平方米
【分析】可先将左上的草坪先向下,再向右分别平移2米,从而将两部分的草坪组成一个长方形,通过平移可知,草坪的面积=长(22-2)米,宽(14-2)米的长方形的面积,长方形的面积=长×宽,依此画图并解答即可。
【详解】画图如下:
22-2=20(米)
14-2=12(米)
20×12=240(平方米)
答:草坪的面积是240平方米。
【点睛】此题考查的是通过平移的方法计算出图形的面积,应熟练掌握平移图形的方法,以及长方形的面积的计算方法。
5.左;7;
下;4;
结果一样,描述不一样;
【分析】平移是指在同一个平面内,如果一个图形上的所有点都按照某个直线方向做相同距离的移动,那么这样的图形运动就叫做图形的平移运动,简称平移,平移不改变图形的形状和大小,依此根据平移的方向和距离填空并解答即可。
【详解】根据分析,填空如下:
答:两种平移结果一样,描述不一样
【点睛】熟练掌握平移的特点,是解答此题的关键。
6.(1)左;6;(2)见详解;(3)见详解
【分析】(1)根据图①虚线与实线图形的相对位置及箭头指向、对应部分之间的距离(格数)即可确定平移的方向和距离(格数)。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图③的关键对称点,依次连接即可。
(3)想要画出图②原来的位置,则要将图②向右平移5格,根据平移的特征,把图2的各顶点分别向右平移5格,依次连接即可得到原来的位置。
【详解】(1)图①向左平移了6格;
(2)画出图③的另一半,使它成为一个轴对称图形如下图;
(3)图②是一个图形向左平移5格得到的,“我”知道这个图形的原来位置,如下图:
【点睛】图形平移注意三要素:即原位置、平移方向、平移距离。求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连接各对称点即可。
7.6分钟
【分析】根据图示,利用平移的方法可得李明走的路程等于长方形的长和宽的和;然后根据路程÷时间=速度,用252除以3,求出他每分钟走多少米;最后用剩下的路程除以他的速度,即可求出李明还要走多少分钟才能到达图书馆。
【详解】(450+306-252)÷(252÷3)
=(756-252)÷84
=504÷84
=6(分钟)
答:李明还要走6分钟才能到达图书馆。
【点睛】本题考查的知识点:①平移求总路程;②行程问题。行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
8.(1)见详解
(2)上(或右);1(或5);右(或上);5(或1);6
(3)见详解
【分析】(1)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底;据此画出三角形的高即可。
(2)观察图2可知,将图2先向上(或右)平移1(或5)格,再向右(或上)平移5(或1)格后能与图3拼成一个长方形,这个长方形的长是3厘米、宽是2厘米,所以它的面积是(3×2)平方厘米。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图4的关键点的对称点,依次连结即可。
【详解】(1)根据三角形的高的定义,画三角形ABO指定底边上的高,如下:
(2)3×2=6(平方厘米)
所以,把图2先向上(或右)平移1(或5)格,再向右(或上)平移5(或1)格后能与图3拼成一个长方形,这个长方形的面积是6平方厘米。
(3)补全图4这个轴对称图形,如下:
【点睛】本题主要考查了三角形高的定义、补全轴对称图形及画平移后的图形,是据此知识,熟练掌握灵活运用。
9.10米
【详解】试题分析:利用对称把原图变成一个正方形,如下图.
正方形的边长为:20×2÷4=10(米) AB为:10÷2=5(米),据此即可得解.
解:据分析可知:
BC的长度为:
20×2÷4=10(米)
答:要使所建的鸡舍面积最大,BC的长应是10米.
点评:此题主要考查依据轴对称图形的概念及特征解决实际问题.
10.1小时15分
【分析】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称,弄清红红实际是什么时刻开始做,什么时刻做完,用做完的时刻减去开始做的时刻就是她做试卷用的时间。
【详解】如图,
红红8时50分开始做试卷,10时05分做完。
10时05分﹣8时50分=1小时15分
答:红红用了1小时15分。
【点睛】此题是考查镜面对称、时间的推算;关键弄清实际开始做的时刻和做完的时刻,结束时刻-起始时刻=经过时间。
本专题主要针对正负数相关的内容进行逐层巩固拔高拓展,包括:
1.轴对称
2.平移
2024年二升三数学暑假专题训练 专题07:万以内数的认识(人教版): 这是一份2024年二升三数学暑假专题训练 专题07:万以内数的认识(人教版),共10页。试卷主要包含了下面各数中一个零都不读的是,由4个千和4个十组成的数是等内容,欢迎下载使用。
2024年二升三数学暑假专题训练 专题03:图形的运动(一)(人教版): 这是一份2024年二升三数学暑假专题训练 专题03:图形的运动(一)(人教版),共11页。试卷主要包含了下面标志牌中,是轴对称图形,下列属于旋转现象的是,下面幅图是由下边图形平移得到的,长方形有条对称轴,钟表指针的运动是,先观察,再涂一涂等内容,欢迎下载使用。
2024年三升四数学暑假专题训练 专题07:小数的初步认识(人教版): 这是一份2024年三升四数学暑假专题训练 专题07:小数的初步认识(人教版),共9页。试卷主要包含了0.4元表示,3.75读作,□.5<4.8,□里填的数有个,列竖式计算等内容,欢迎下载使用。













