北师大版初中九年级数学上册第一章素养提优测试卷课件

这是一份北师大版初中九年级数学上册第一章素养提优测试卷课件，共41页。

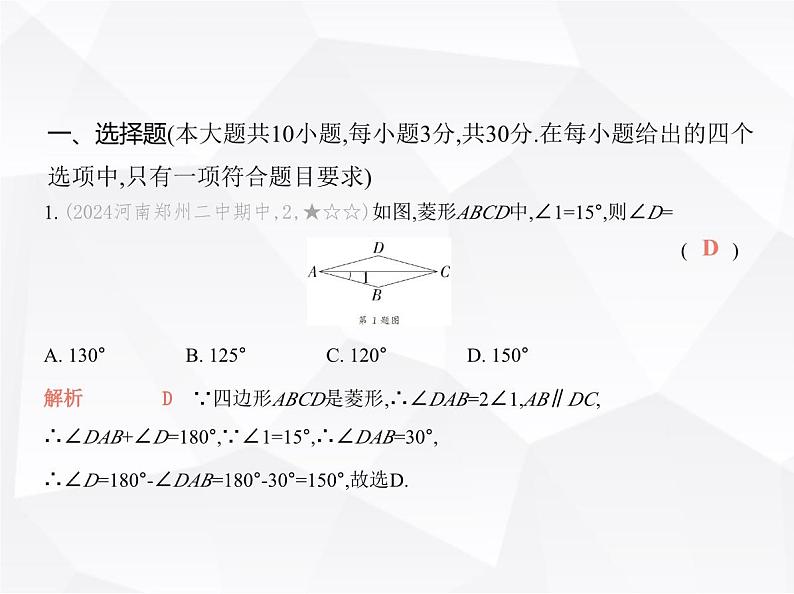
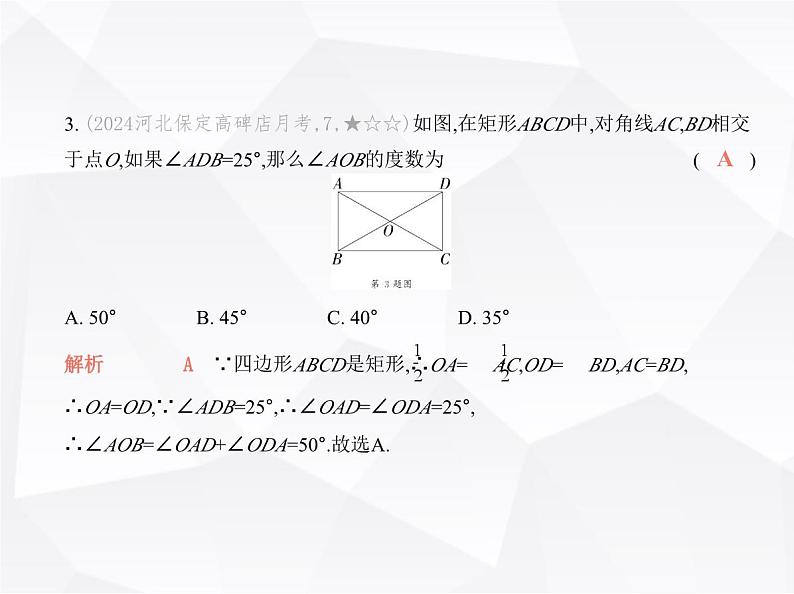
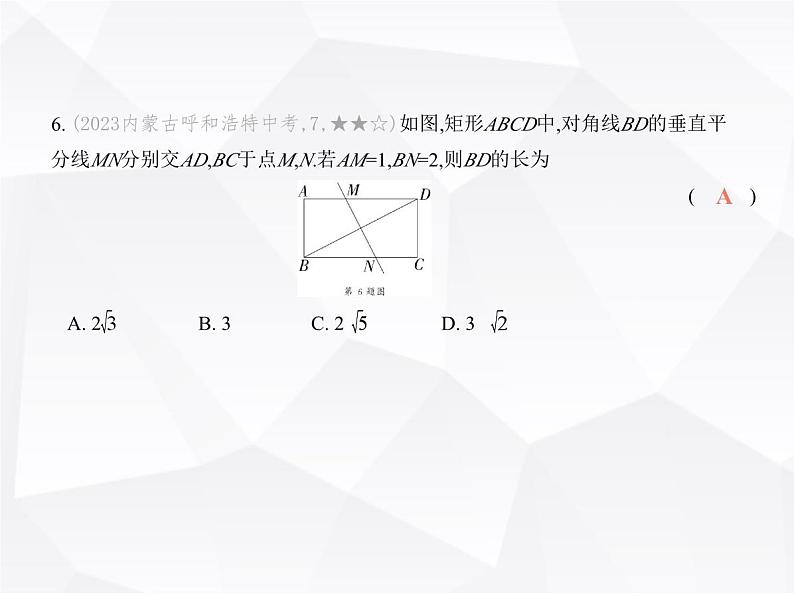
第一章　素养提优测试卷(时间:90分钟　满分:120分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求)1. (2024河南郑州二中期中,2,★☆☆)如图,菱形ABCD中,∠1=15°,则∠D= ( )DA. 130°　　　    B. 125°　　　    C. 120°　　　    D. 150°解析    D　∵四边形ABCD是菱形,∴∠DAB=2∠1,AB∥DC,∴∠DAB+∠D=180°,∵∠1=15°,∴∠DAB=30°,∴∠D=180°-∠DAB=180°-30°=150°,故选D. 2. (★☆☆)下列条件中能判定一个四边形是正方形的是  ( )A. 三个角是直角的四边形B. 对角线互相垂直的平行四边形C. 对角线互相垂直的矩形D. 有一个角是直角的平行四边形C解析    C    A.三个角是直角的四边形是矩形,不符合题意;B.对角线互相垂直的平行四边形是菱形,不符合题意;C.对角线互相垂直的矩形是正方形,符合题意;D.有一个角是直角的平行四边形是矩形,不符合题意.故选C.3. (2024河北保定高碑店月考,7,★☆☆)如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠ADB=25°,那么∠AOB的度数为     ( )AA. 50°　　　    B. 45°　　　    C. 40°　　　    D. 35°4. (2024河北保定高碑店月考,9,★☆☆)如图,四边形ABCD是平行四边形,下列结论中错误的是     ( )A. 当AB=BC时,它是正方形　　　    B. 当AC⊥BD时,它是菱形C. 当AC=BD时,它是矩形　　　    D. 当∠ABC=90°时,它是矩形解析    A　∵四边形ABCD是平行四边形,∴当AB=BC时,平行四边形ABCD是菱形,不一定是正方形,故选项A错误,符合题意;当AC⊥BD时,平行四边形ABCD是菱形,故选项B正确,不符合题意;当AC=BD时,平行四边形ABCD是矩形,故选项C正确,不符合题意;当∠ABC=90°时,平行四边形ABCD是矩形,故选项D正确,不符合题意.故选A.A5. [学科素养　应用意识](2024陕西西安期末,2,★★☆)我们常常在建筑物中看到四边形的元素.如图,墙面上砌出的菱形窗户的边长为1米(边框宽度忽略不计),其中较小的内角为60°,则该菱形窗户的采光面积为     ( )BA. 4平方米　　　    B.  平方米　　　    C. 1平方米　　　    D.  平方米6. (2023内蒙古呼和浩特中考,7,★★☆)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=1,BN=2,则BD的长为      ( )AA. 2 　　　    B. 3　　　    C. 2 　　　    D. 3 7. (2024广东佛山三水中学附中月考,8,★★☆)工人师傅在制作矩形窗框时,分三个步骤进行:(1)如图①,先截出两对符合规格的木条,使AB=CD,EF=GH;(2)摆成如图②所示的四边形;(3)    　    　　　    ,矩形窗框制作完成.下列方法中不能作为制作工序的第(3)个步骤的是     ( )A. 将直角尺紧靠窗框一个角,调整窗框的边框使得直角尺的两条直角边与窗框无缝隙B. 调整窗框的边框使得两条对角线长度相等C. 调整窗框的边框使得两条对角线互相垂直D. 调整窗框的边框使得两条对角线与CD边的夹角相等C解析    C　∵AB=CD,EF=GH,∴四边形ABDC是平行四边形.A.将直角尺紧靠窗框一个角,调整窗框的边框使得直角尺的两条直角边与窗框无缝隙,根据有一个角是直角的平行四边形是矩形,可知四边形ABDC是矩形,故该选项不符合题意;B.调整窗框的边框使得两条对角线长度相等,根据对角线相等的平行四边形是矩形,可知四边形ABDC是矩形,故该选项不符合题意;C.调整窗框的边框使得两条对角线互相垂直,此时无法判定四边形ABDC是矩形,故该选项符合题意;D.调整窗框的边框使得两条对角线与CD边的夹角相等,此时可以证明对角线相等,可知四边形ABDC是矩形,故该选项不符合题意.故选C.8. (2023山东青岛大学附中月考,4,★★☆)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为  ( )DA. (2, )　　　    B. ( ,2) C. ( ,3)　　　    D. (3, )9. (2024重庆八中期末,9,★★☆)如图,在菱形ABCD中,对角线AC与BD相交于点O,P是AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=8,BD=6,则PE+PF的值为  ( )CA.  　　　    B.  　　　    C.  　　　    D.   10. [学科素养　推理能力](2022浙江宁波中考,10,★★★)将两张全等的矩形纸片和另两张全等的正方形纸片按如图所示的方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出  ( )A. 正方形纸片的面积　　　    B. 四边形EFGH的面积C. △BEF的面积　　　    D. △AEH的面积C二、填空题(本大题共6小题,每小题4分,共24分)11. (2022黑龙江齐齐哈尔中考,12,★☆☆)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,可添加的条件是    .(写出一个即可)AB=CD12. (2024四川成都期中,12,★★☆)如图,四边形ABCD是菱形,∠DAB=40°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=        度.2013. (2024河南郑州嵩阳中学月考,11,★★☆)如图,连接四边形ABCD各边中点,得到四边形EFGH,当AC、BD满足     　　　    时,才能保证四边形EFGH是矩形.AC⊥BD　　当四边形ABCD的对角线相等时,如图2,该四边形的中点四边形EFGH为菱形.由“中点四边形”模型可知,四边形EFGH为平行四边形,再通过中位线定理,可证明EH=EF,即可证明中点四边形EFGH是菱形.14. (新独家原创,★★☆)如图,在边长为15的菱形ABCD中,E为对角线BD上的任意一点,过E作EF⊥AB于F,EG⊥AD于G,若BD=24,则EF+EG=     　　　    .    14.415. (2022辽宁鞍山中考,14,★★☆)如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC与BD交于点O,E为OB中点,F为AD中点,连接EF,则EF的长为       .答案      16. [方程思想](2022江苏无锡中考,16,★★★)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=    　　　    .1三、解答题(本大题共6小题,共66分)17. (2023山东青岛月考,15,★☆☆)(8分)用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:点O在∠MAN的平分线AP上.求作:菱形ABCD,使∠MAN为菱形的一个内角,点B在AN上,且点O为菱形的对称中心. 18. (2024辽宁辽阳期末,19,★★☆)(10分)如图①,在Rt△ABC中,∠ACB=90°,点D是AB的中点.求证:CD= AB.下面是两位同学添加辅助线的方法:小星:如图②,延长CD到点E,使得DE=CD,连接AE,BE;小红:如图③,取BC的中点E,连接DE.请选择一位同学的方法,完成证明.第18题图19. (2024山西太原期末,18,★★☆)(10分)如图,已知矩形ABCD中,∠BAD和∠ADC的平分线交于BC边上一点E.点F为矩形外一点,四边形AEDF为平行四边形.求证:四边形AEDF是正方形.20. (2024贵州六盘水期中,23,★★☆)(12分)下面是多媒体上的一道试题:如图,在菱形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接BD,DF.求证:四边形BFDE是矩形.小星和小红分别给出了自己的思路.小星:先证明四边形BFDE是平行四边形,然后利用矩形定义即可得证;小红:先证明△ADF与△CBE全等,然后利用“有三个角是直角的四边形是矩形”即可得证.  (1)请你选择一位同学的思路,并进行证明.(2)若BD=2 ,BE=4,求BC的长.解析    (1)选择小星的思路.证明:∵四边形ABCD是菱形,∴AB=CD,AB∥CD.∵AF=CE,∴BF=DE,∴四边形BFDE是平行四边形.∵CD⊥BE,∴∠BED=90°,∴四边形BFDE是矩形.选择小红的思路.证明:∵四边形ABCD是菱形,∴AD=BC,∠A=∠C.∵AF=CE,∴△ADF≌△CBE(SAS),∴∠AFD=∠CEB=90°,∴∠DFB=90°.∵CD∥AB,∴∠FBE=∠CEB=90°,21. (2023甘肃兰州中考,24,★★☆)(12分)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD,AD于点F,G,连接DE.    (1)判断四边形OCDE的形状,并说明理由.(2)当CD=4时,求EG的长.22. (2024辽宁辽阳期末,23,★★★)(14分)综合与实践数学活动课上,同学们以“正方形与旋转”为主题开展探究活动.【探索发现】(1)如图①,在正方形ABCD中,点E是边CD上一点,AF⊥BE于点F,将线段AF绕点A逆时针旋转90°得到线段AG,连接DG,可证得△ABF≌△ADG.请写出证明过程.【深入思考】(2)在(1)的条件下,如图②,延长BE,GD交于点H,试猜想线段BF,FH,DH之间的数量关系,并证明你的猜想.【拓展延伸】(3)在(2)的条件下,如图③,连接CH,将线段DH绕点H逆时针旋转90°得到线段HP,点P在BH上,试猜想BP与CH的数量关系,并证明你的猜想.第22题图解析    (1)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵将线段AF绕点A逆时针旋转90°得到线段AG,∴∠GAF=90°,AG=AF,∴∠GAF=∠DAB,∴∠GAD=∠BAF,∴△ABF≌△ADG(SAS).