




还剩33页未读,
继续阅读
所属成套资源:全套北师大版初中九年级数学上册素养基础测试+综合测试课件
成套系列资料,整套一键下载
北师大版初中九年级数学上册第四章素养提优测试卷课件
展开
这是一份北师大版初中九年级数学上册第四章素养提优测试卷课件,共41页。
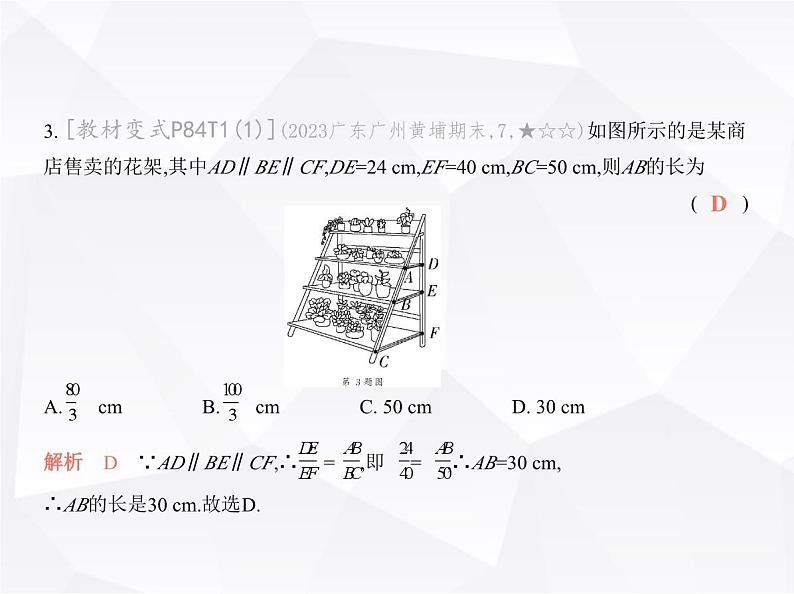
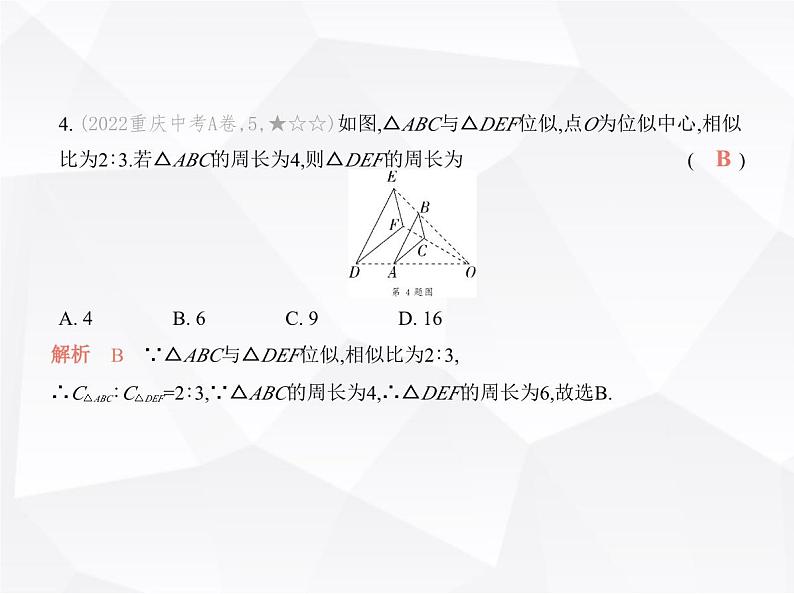
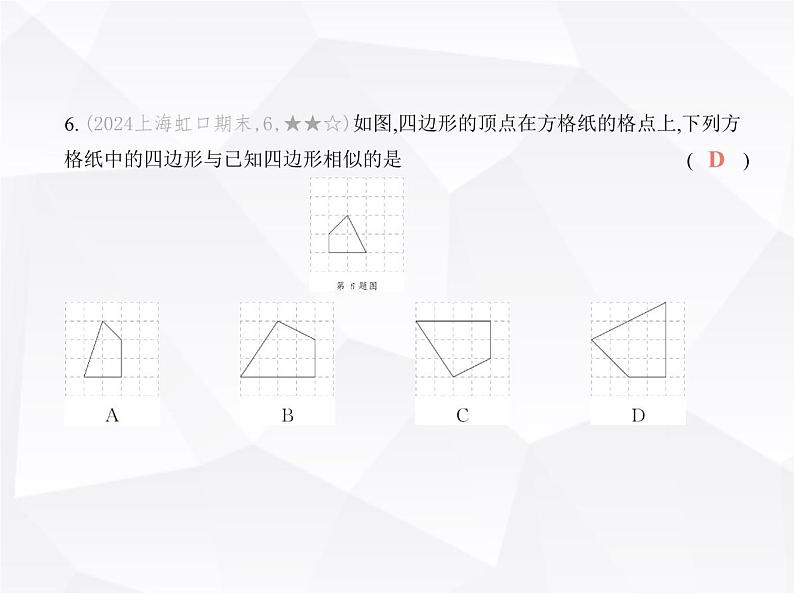
第四章 素养提优测试卷(时间:90分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求)1. (2024陕西西安未央期末,1,★☆☆)已知 = ,则 = ( )A. B. C. D. D2. [教材变式P79随堂练习T3](2023吉林北京师大长春附属学校期末,2,★☆☆)下列四组线段中,是成比例线段的一组是 ( )A. a=1,b=2,c=3,d=4 B. a=1,b= ,c= ,d= C. a=5,b=6,c=7,d=8 D. a=4,b=6,c=6,d=8B3. [教材变式P84T1(1)](2023广东广州黄埔期末,7,★☆☆)如图所示的是某商店售卖的花架,其中AD∥BE∥CF,DE=24 cm,EF=40 cm,BC=50 cm,则AB的长为 ( )A. cm B. cm C. 50 cm D. 30 cmD4. (2022重庆中考A卷,5,★☆☆)如图,△ABC与△DEF位似,点O为位似中心,相似 比为2∶3.若△ABC的周长为4,则△DEF的周长为 ( )A. 4 B. 6 C. 9 D. 16B解析 B ∵△ABC与△DEF位似,相似比为2∶3,∴C△ABC∶C△DEF=2∶3,∵△ABC的周长为4,∴△DEF的周长为6,故选B.5. (2024河北唐山乐亭期末,10,★★☆)如图,在三角形纸片ABC中,∠A=76°,∠B= 34°.将纸片沿某处剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是 ( )A. ①② B. ②④ C. ①③ D. ③④C解析 C 题图①中,∠B=∠B,∠A=∠BDE=76°,所以阴影三角形和△ABC相似;题图②中,根据已知不能判定阴影三角形和△ABC相似;题图③中,∠C=∠C,∠B=∠CED=34°,所以阴影三角形和△CAB相似;题图④中,根据已知不能判定阴影三角形和△ABC相似.所以阴影三角形与原三角形相似的有①③,故选C.6. (2024上海虹口期末,6,★★☆)如图,四边形的顶点在方格纸的格点上,下列方 格纸中的四边形与已知四边形相似的是 ( )D7. [学科素养 几何直观](2024广东深圳外国语学校月考,6,★★☆)如图,已知矩形OABC∽矩形OA′B′C′,B′ (10,5),AA′=1,则CC′的长是 ( )A. 1 B. 2 C. 3 D. 4B8. (2023山东济南历下期中,9,★★☆)图①是小玉制作的简易投石机的示意图, GP是杠杆,点A为支点,AD=AC,支架AH垂直于地面BC,且AH=CD=2.如图②,当投 石机准备时,点G恰好与点B重合,此时AG和AC互相垂直,则线段AG= ( )B第8题图9. (2023山东济南中考,9,★★☆)如图,在△ABC中,AB=AC,∠BAC=36°,以点C为 圆心,以BC为半径作弧交AC于点D,再分别以B,D为圆心,以大于 BD的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE.以下结论不正确的是 ( )CA. ∠BCE=36° B. BC=AEC. = D. = 10. (2022河南郑州外国语学校期中,10,★★★)如图,在矩 形ABCD中,AB=2,CB=4,连接AC,以对角线AC为边,按逆时针方向作矩形ACC1B1, 使矩形ACC1B1∽矩形ADCB;再连接AC1,以对角线AC1为边,按逆时针方向作矩形 AC1C2B2,使矩形AC1C2B2∽矩形ACC1B1;……,按照此规律作下去.若矩形ABCD的 面积记作S1,矩形ACC1B1的面积记作S2,矩形AC1C2B2的面积记作S3,……,则S2 021的 值为 ( )A. 4× B. 8× C. 4× D. 8× D二、填空题(本大题共6小题,每小题4分,共24分)11. (2024陕西咸阳市实验中学期中,11,★☆☆)如图,在小提琴的 设计中,蕴含着数学知识,AC,BC,AB各部分长度的比满足 = = ,已知AB=56 cm,则BC的长为 cm.(结果保留根号) 12. (2023山东青岛市南期中,11,★☆☆)如图,已知l1∥l2∥l3,AB=6 cm,BC=3 cm,A1B1=4 cm,则线段B1C1= cm.213. [一题多解](2024四川绵阳涪城期末,13,★☆☆)若 = = 且a-b+c=2,则a+b-c的值为 . 对应目标编号M910400114. (2024内蒙古包头东河期末,16,★★☆)如图,将一副三角板按如图所示的方式 叠放,则 的值为 .答案 15. (2023辽宁沈阳南昌中学期中,13,★★☆)如图,在△ABC中,AD⊥BC,垂足为D, AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都 在△ABC的边上,那么△AEM与四边形BCME的面积比为 .1∶3答案 1∶316. (2023山东青岛五中期末,16,★★★)如图,(n+1)个边长 为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面 积为S2,……,△Bn+1DnCn 的面积为Sn,则Sn= (用含n的式子表示).三、解答题(本大题共6小题,共66分)17. (2023四川自贡荣县月考,20,★☆☆)(10分)如图,△ABC的顶点都在网格点上, 点M的坐标为(0,1). (1)以点O为位似中心,把△ABC按2∶1进行放大,在y轴的左侧,画出放大后的△ DEF(D、E、F分别是A、B、C的对应点).(2)点D的坐标是 .(3)S△ABO∶S四边形ABED= . 18. (新独家原创,★★☆)(10分)翻花绳是中国传统的民间益智游戏,图①是翻花 的一种图案,可以抽象成图②,且AF∥EC,DE∥BF,求证: = . 第18题图19. (2023山西晋中期末,20,★★☆)(10分)如图,强强同学为了测 量学校一座高楼OE的高度,在操场上点A处放一面平面镜,从点A处后退1 m到达 点B处,恰好在平面镜中看到高楼的顶部点E的像,再将平面镜向后移动4 m(即AC =4 m)放在点C处,从点C处后退1.5 m到达点D处,恰好再次在平面镜中看到高楼 的顶部点E的像,测得强强同学的眼睛距地面的高度为1.5 m.已知点O,A,B,C,D在 同一水平线上,且GD,FB,EO均与OD垂直.求高楼OE的高度.(平面镜的厚度忽略 不计) 20. [学科素养 推理能力](2022山东泰安中考,23,★★☆)(10分)如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F. (1)若BE平分∠CBD,求证:BF⊥AC.(2)找出图中与△OBF相似的三角形,并说明理由.(3)若OF=3,EF=2,求DE的长度.21. (2023山西临汾安泽期末,19,★★☆)(12分)阅读与思考:凸透镜在我们的生活 中有着广泛的应用,如照相机和望远镜.凸透镜成像规律是一种光学定律.在光学 中,由实际光线会聚而成,且能在光屏上呈现的像称为实像.凸透镜成像公式也被 称为高斯成像公式,其形式为 = + .图①是蜡烛成像的光路图,其中f为焦距,u为物距,v为像距.现将图①的光路图抽象为图②所示的数学几何图形,蜡烛AC发 出的光线CE平行于直线AB,光线CE经过凸透镜MN后,经过焦点F与经过凸透镜 中心O的光线交于点D,其中物距AO=u,像距BO=v,焦距OF=f,四边形AOEC是矩 形,DB⊥AB,MN⊥AB. (1)请根据图②提供的信息,用所学数学知识证明高斯成像公式.(2)当凸透镜的焦距为10 cm,把物体放在离凸透镜30 cm处时,所成的像离凸透镜 的距离为 .22. (2024山东济南槐荫期中,23,★★★)(14分)【问题背景】△ABC中,AB=AC,∠ BAC=90°,P为BC上的动点,小熙拿含45°角的透明三角板,使45°角的顶点落在 点P,三角板可绕P点旋转. 对应目标编号M9104005【用数学的眼光观察】(1)如图①,当三角板的两边分别交AB、AC于点E、F时,以下结论正确的是 .①△BPE≌△CFP;②△BPE∽△CFP;③∠BEP=∠CPF;④ = .【用数学的思维思考】(2)将三角板绕点P旋转到图②的位置,三角板的两边分别交BA的延长线、边AC 于点E、F.△BPE与△CFP相似吗?请说明理由.【用数学的语言表达】(3)在(2)的条件下,连接EF,动点P运动到什么位置时,△BPE∽△PFE?说明理由.解析 (1)∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴∠BEP=180°-45°-∠BPE=135°-∠BPE,∵∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,∴△BEP∽△CPF,∴ = ,∵PE与FP不一定相等,∴△BPE与△CFP不一定全等,故①错误,②正确,③正确,④正确,故答案为②③④.(2)△BPE∽△CFP,理由:∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴∠BEP=180°-45°-∠BPE=135°-∠BPE,∵∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,∴△BPE∽△CFP.(3)当点P为BC的中点时,△BPE∽△PFE,理由:如图,∵△BPE∽△CFP,∴ = ,∵P为BC的中点,∴CP=PB,∴ = ,∴ = ,∵∠B=∠EPF,∴△BPE∽△PFE.
第四章 素养提优测试卷(时间:90分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求)1. (2024陕西西安未央期末,1,★☆☆)已知 = ,则 = ( )A. B. C. D. D2. [教材变式P79随堂练习T3](2023吉林北京师大长春附属学校期末,2,★☆☆)下列四组线段中,是成比例线段的一组是 ( )A. a=1,b=2,c=3,d=4 B. a=1,b= ,c= ,d= C. a=5,b=6,c=7,d=8 D. a=4,b=6,c=6,d=8B3. [教材变式P84T1(1)](2023广东广州黄埔期末,7,★☆☆)如图所示的是某商店售卖的花架,其中AD∥BE∥CF,DE=24 cm,EF=40 cm,BC=50 cm,则AB的长为 ( )A. cm B. cm C. 50 cm D. 30 cmD4. (2022重庆中考A卷,5,★☆☆)如图,△ABC与△DEF位似,点O为位似中心,相似 比为2∶3.若△ABC的周长为4,则△DEF的周长为 ( )A. 4 B. 6 C. 9 D. 16B解析 B ∵△ABC与△DEF位似,相似比为2∶3,∴C△ABC∶C△DEF=2∶3,∵△ABC的周长为4,∴△DEF的周长为6,故选B.5. (2024河北唐山乐亭期末,10,★★☆)如图,在三角形纸片ABC中,∠A=76°,∠B= 34°.将纸片沿某处剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是 ( )A. ①② B. ②④ C. ①③ D. ③④C解析 C 题图①中,∠B=∠B,∠A=∠BDE=76°,所以阴影三角形和△ABC相似;题图②中,根据已知不能判定阴影三角形和△ABC相似;题图③中,∠C=∠C,∠B=∠CED=34°,所以阴影三角形和△CAB相似;题图④中,根据已知不能判定阴影三角形和△ABC相似.所以阴影三角形与原三角形相似的有①③,故选C.6. (2024上海虹口期末,6,★★☆)如图,四边形的顶点在方格纸的格点上,下列方 格纸中的四边形与已知四边形相似的是 ( )D7. [学科素养 几何直观](2024广东深圳外国语学校月考,6,★★☆)如图,已知矩形OABC∽矩形OA′B′C′,B′ (10,5),AA′=1,则CC′的长是 ( )A. 1 B. 2 C. 3 D. 4B8. (2023山东济南历下期中,9,★★☆)图①是小玉制作的简易投石机的示意图, GP是杠杆,点A为支点,AD=AC,支架AH垂直于地面BC,且AH=CD=2.如图②,当投 石机准备时,点G恰好与点B重合,此时AG和AC互相垂直,则线段AG= ( )B第8题图9. (2023山东济南中考,9,★★☆)如图,在△ABC中,AB=AC,∠BAC=36°,以点C为 圆心,以BC为半径作弧交AC于点D,再分别以B,D为圆心,以大于 BD的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE.以下结论不正确的是 ( )CA. ∠BCE=36° B. BC=AEC. = D. = 10. (2022河南郑州外国语学校期中,10,★★★)如图,在矩 形ABCD中,AB=2,CB=4,连接AC,以对角线AC为边,按逆时针方向作矩形ACC1B1, 使矩形ACC1B1∽矩形ADCB;再连接AC1,以对角线AC1为边,按逆时针方向作矩形 AC1C2B2,使矩形AC1C2B2∽矩形ACC1B1;……,按照此规律作下去.若矩形ABCD的 面积记作S1,矩形ACC1B1的面积记作S2,矩形AC1C2B2的面积记作S3,……,则S2 021的 值为 ( )A. 4× B. 8× C. 4× D. 8× D二、填空题(本大题共6小题,每小题4分,共24分)11. (2024陕西咸阳市实验中学期中,11,★☆☆)如图,在小提琴的 设计中,蕴含着数学知识,AC,BC,AB各部分长度的比满足 = = ,已知AB=56 cm,则BC的长为 cm.(结果保留根号) 12. (2023山东青岛市南期中,11,★☆☆)如图,已知l1∥l2∥l3,AB=6 cm,BC=3 cm,A1B1=4 cm,则线段B1C1= cm.213. [一题多解](2024四川绵阳涪城期末,13,★☆☆)若 = = 且a-b+c=2,则a+b-c的值为 . 对应目标编号M910400114. (2024内蒙古包头东河期末,16,★★☆)如图,将一副三角板按如图所示的方式 叠放,则 的值为 .答案 15. (2023辽宁沈阳南昌中学期中,13,★★☆)如图,在△ABC中,AD⊥BC,垂足为D, AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都 在△ABC的边上,那么△AEM与四边形BCME的面积比为 .1∶3答案 1∶316. (2023山东青岛五中期末,16,★★★)如图,(n+1)个边长 为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面 积为S2,……,△Bn+1DnCn 的面积为Sn,则Sn= (用含n的式子表示).三、解答题(本大题共6小题,共66分)17. (2023四川自贡荣县月考,20,★☆☆)(10分)如图,△ABC的顶点都在网格点上, 点M的坐标为(0,1). (1)以点O为位似中心,把△ABC按2∶1进行放大,在y轴的左侧,画出放大后的△ DEF(D、E、F分别是A、B、C的对应点).(2)点D的坐标是 .(3)S△ABO∶S四边形ABED= . 18. (新独家原创,★★☆)(10分)翻花绳是中国传统的民间益智游戏,图①是翻花 的一种图案,可以抽象成图②,且AF∥EC,DE∥BF,求证: = . 第18题图19. (2023山西晋中期末,20,★★☆)(10分)如图,强强同学为了测 量学校一座高楼OE的高度,在操场上点A处放一面平面镜,从点A处后退1 m到达 点B处,恰好在平面镜中看到高楼的顶部点E的像,再将平面镜向后移动4 m(即AC =4 m)放在点C处,从点C处后退1.5 m到达点D处,恰好再次在平面镜中看到高楼 的顶部点E的像,测得强强同学的眼睛距地面的高度为1.5 m.已知点O,A,B,C,D在 同一水平线上,且GD,FB,EO均与OD垂直.求高楼OE的高度.(平面镜的厚度忽略 不计) 20. [学科素养 推理能力](2022山东泰安中考,23,★★☆)(10分)如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F. (1)若BE平分∠CBD,求证:BF⊥AC.(2)找出图中与△OBF相似的三角形,并说明理由.(3)若OF=3,EF=2,求DE的长度.21. (2023山西临汾安泽期末,19,★★☆)(12分)阅读与思考:凸透镜在我们的生活 中有着广泛的应用,如照相机和望远镜.凸透镜成像规律是一种光学定律.在光学 中,由实际光线会聚而成,且能在光屏上呈现的像称为实像.凸透镜成像公式也被 称为高斯成像公式,其形式为 = + .图①是蜡烛成像的光路图,其中f为焦距,u为物距,v为像距.现将图①的光路图抽象为图②所示的数学几何图形,蜡烛AC发 出的光线CE平行于直线AB,光线CE经过凸透镜MN后,经过焦点F与经过凸透镜 中心O的光线交于点D,其中物距AO=u,像距BO=v,焦距OF=f,四边形AOEC是矩 形,DB⊥AB,MN⊥AB. (1)请根据图②提供的信息,用所学数学知识证明高斯成像公式.(2)当凸透镜的焦距为10 cm,把物体放在离凸透镜30 cm处时,所成的像离凸透镜 的距离为 .22. (2024山东济南槐荫期中,23,★★★)(14分)【问题背景】△ABC中,AB=AC,∠ BAC=90°,P为BC上的动点,小熙拿含45°角的透明三角板,使45°角的顶点落在 点P,三角板可绕P点旋转. 对应目标编号M9104005【用数学的眼光观察】(1)如图①,当三角板的两边分别交AB、AC于点E、F时,以下结论正确的是 .①△BPE≌△CFP;②△BPE∽△CFP;③∠BEP=∠CPF;④ = .【用数学的思维思考】(2)将三角板绕点P旋转到图②的位置,三角板的两边分别交BA的延长线、边AC 于点E、F.△BPE与△CFP相似吗?请说明理由.【用数学的语言表达】(3)在(2)的条件下,连接EF,动点P运动到什么位置时,△BPE∽△PFE?说明理由.解析 (1)∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴∠BEP=180°-45°-∠BPE=135°-∠BPE,∵∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,∴△BEP∽△CPF,∴ = ,∵PE与FP不一定相等,∴△BPE与△CFP不一定全等,故①错误,②正确,③正确,④正确,故答案为②③④.(2)△BPE∽△CFP,理由:∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴∠BEP=180°-45°-∠BPE=135°-∠BPE,∵∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,∴△BPE∽△CFP.(3)当点P为BC的中点时,△BPE∽△PFE,理由:如图,∵△BPE∽△CFP,∴ = ,∵P为BC的中点,∴CP=PB,∴ = ,∴ = ,∵∠B=∠EPF,∴△BPE∽△PFE.
相关资料
更多









