






还剩34页未读,
继续阅读
所属成套资源:全套北师大版初中九年级数学上册课时教学课件
成套系列资料,整套一键下载
北师大版初中九年级数学上册第五章投影与视图素养综合检测课件
展开
这是一份北师大版初中九年级数学上册第五章投影与视图素养综合检测课件,共42页。
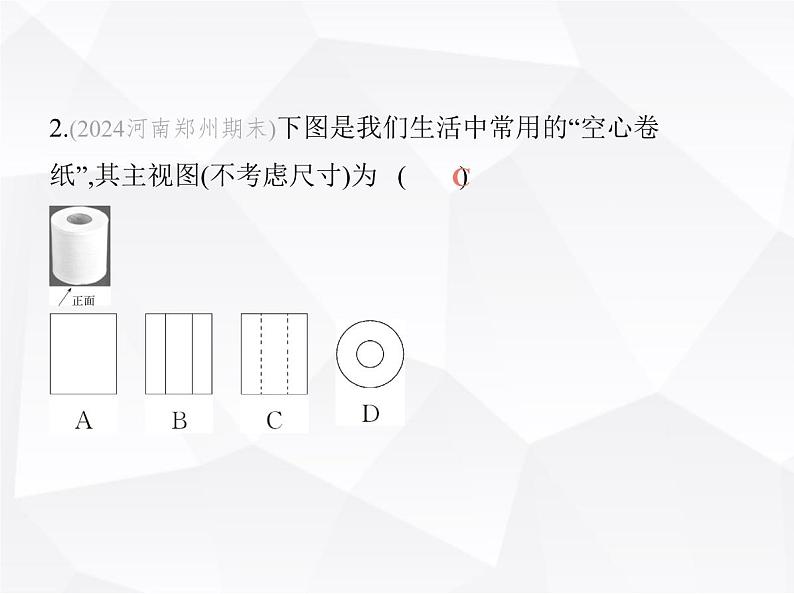
第五章 素养综合检测(满分100分, 限时90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.(情境题·中华优秀传统文化)(2024广东清远期末)日晷是我 国古代利用日影测定时刻的一种计时仪器,它由“晷面”和 “晷针”组成.当太阳光照在日晷上时,晷针的影子就会投向 晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以 此来显示时刻.晷针在晷面上形成的投影是( )A.中心投影BB.平行投影C.既是平行投影又是中心投影D.不能确定解析 晷针在晷面上形成的投影是由太阳光线照射形成的, 故形成的投影是平行投影.2.(2024河南郑州期末)下图是我们生活中常用的“空心卷 纸”,其主视图(不考虑尺寸)为 ( ) C解析 观察图形可知,该几何体的主视图如图: 故选C.3.(2024四川渠县期末)由5个大小相同的小正方体搭成的几 何体如图所示,关于它的视图,下列说法正确的是 ( ) A.主视图的面积最小B.左视图的面积最小C.俯视图的面积最小D.从三个方向看的视图面积相等C解析 由题意可知,主视图有5个小正方形,俯视图有3个小正 方形,左视图有5个小正方形,所以俯视图的面积最小.4.(2024吉林白山临江期末)若在同一盏路灯下,小明与小强 的影子一样长,则下列说法正确的是 ( )A.小明比小强的个子高B.小强比小明的个子高C.两个人的个子一样高D.无法判断谁的个子高D解析 因为小明与小强所处的位置不确定,所以无法判断谁 的个子高.故选D.5.(2024广西凤山期末)下列立体图形中,主视图和左视图均 为三角形的是 ( ) C解析 A.主视图为矩形,左视图为矩形,故本选项不合题 意;B.主视图为矩形,左视图为矩形,故本选项不合题意;C.主 视图和左视图均为三角形,故本选项符合题意;D.主视图为一 个矩形,矩形中间有一条竖直的实线,左视图为矩形,故本选 项不合题意.故选C.6.(情境题·中华优秀传统文化)(2023山东潍坊中考)在我国古 代建筑中经常使用榫卯构件,如图所示的是某种榫卯构件的 示意图,其中卯的俯视图是 ( ) C解析 由题图可知俯视图为 .故选C.7.(新考法)(2023内蒙古包头期末)如图,通过两人的对话,我们 可以判断他们共同搭的几何体是 ( ) D解析 本题从两人对话中给出的信息进行判断,选项A,主视图和左视图不一样,故不符合题意;选项B,只有5个正方体,故不符合题意;选项C,主视图和左视图不一样,故不符合题意;选项D,主视图和左视图一样,且有6个正方体,故符合题意.故选D.8.如图,这个几何体是由5个相同的小立方块搭成的,若移走 一个小立方块,左视图发生了改变,则移走的小立方块是( ) A.① B.② C.③ D.④C解析 移走小立方块③后,左视图由两行变成了一行,发生了 改变.故选C.9.(2024山东泰安新泰期末)一个几何体是由一些大小相同的 小正方体组成的,其俯视图与主视图如图所示,则组成这个几 何体的小正方体最多有 ( )A.9个 B.10个 C.11个 D.12个C解析 结合俯视图和主视图知,这个几何体的底层有5个小 正方体,从下向上数第二层,最多有3个小正方体,第3层最多 有3个小正方体,因此组成这个几何体的小正方体最多有5+3 +3=11(个).故选C.10.(2023重庆南岸期末)下图是一个由铁铸灌成的几何体的 三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积 为 ( )A.12π B.18π C.24π D.78πB解析 由三视图可得,这个几何体是空心圆柱,其高为6,底面 小圆的半径是1,大圆的半径是2,故这个几何体的体积为6×π×22-6×π×12=24π-6π=18π.故选B.二、填空题(本大题共6小题,每小题3分,共18分)11.(情境题·中华优秀传统文化)(2024四川成都期末)早在1 00 0多年前的宋朝,手影就已经作为民间一种有趣的游戏而存 在.诗人释惠明在《手影戏》中写道:“三尺生绡作戏台,全 凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏 全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、 飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于 (填“平行投影”或“中心投影”).中心投影12.某天学校举办了运动会,小红先参加了校运动会女子100 m比赛,过一段时间又参加了女子400 m比赛,比赛都在上午 进行,下图是摄影师在同一位置拍摄小红的两张照片,那么 (填“甲”或“乙”)照片是在小红参加400 m比赛时 拍摄的.乙解析 易知在太阳光下从早晨到中午物体的影长由长变短, ∵比赛都在上午进行,先进行的是100 m比赛,∴影子较长的 甲照片是参加100 m比赛时拍摄的,影子较短的乙照片是参 加400 m比赛时拍摄的.13.如图,正方形ABCD的边长是5 cm,以直线AB为轴,将正方 形旋转一周后,所得几何体的左视图的面积是 . 50 cm2 解析 由题意可得,旋转所得几何体的左视图为矩形,且矩形 的宽为5 cm,长为2×5=10 cm,故所得几何体的左视图的面积 为5×10=50(cm2).故答案为50 cm2.14.如图所示,一长方体木板上有两个空洞,一个是正方形形 状的,一个是圆形形状的,对于图中的4种几何体,你觉得哪一 种作为塞子既可以堵住圆形空洞又可以堵住正方形空洞? (填序号). ②解析 ②中圆柱的俯视图是圆,可以堵住圆形空洞,主视图和 左视图是正方形,可以堵住正方形空洞,故答案为②.15.如图,在一次数学活动课上,张明用17个棱长为1的小正方 体搭成了一个几何体,然后他请王亮用其他同样的小正方体 在旁边再搭一个几何体,使王亮所搭几何体的左视图与张明 所搭几何体的左视图相同,那么王亮至少需要 个小 正方体. 7解析 由题可知,张明所搭几何体的左视图有7个小正方形, 故王亮至少需要7个小正方体,故答案为7.16.(2024重庆南岸期末)如图所示的是一个几何体的三视图, 俯视图为正三角形,则该几何体的侧面积为 . 36解析 由三视图知该几何体是一个三棱柱,且该三棱柱的高 为6,底面是一个高为 的正三角形,易知该三棱柱的底面正三角形的边长为2,∴该几何体的侧面积是(2+2+2)×6=36,故 答案为36.三、解答题(共52分)17.(8分)甲、乙两根木杆在同一时刻的影子如图所示.(1)请在图中画出形成木杆影子的光线,并指出是平行投影还 是中心投影.(2)若是路灯的光线,请找出路灯灯泡的位置.(3)请在图中画出木杆丙的影子.解析 (1)光线如图所示,是中心投影.(2)如图所示,点O所在的位置是路灯灯泡的位置.(3)木杆丙的影子如图所示.18.(2024陕西榆林十中期末)(8分)如图所示的是由6块小正方 体搭成的几何体(主视图已给出). (1)请在方格图中画出该几何体的左视图和俯视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图 和左视图不变,最多可以再添加 块小正方体.解析 (1)该几何体的左视图和俯视图如图: (2)2.19.(新独家原创)(8分)吊脚楼是中国南方多个少数民族的传 统民居,尤其在渝东南、桂北、湘西、鄂西、黔东南等地区 较为常见,有的吊脚楼为三层建筑,除了屋顶盖瓦以外,上上 下下全部用杉木建造.屋柱用大杉木凿眼,柱与柱之间用大小 不一的杉木斜穿直套连在一起,尽管不用一个铁钉也十分坚 固.图①和图②是吊脚楼常用的榫卯结构,请分别画出图①和 图②的三视图. 解析 题图①的三视图如图:题图②的三视图如图: 20.(9分)用小立方块搭一个几何体,它的主视图和俯视图如 图所示,俯视图中小正方形中的字母表示在该位置上小立方 块的个数.(1)a= ,b= .(2)这个几何体最少由 个小立方块搭成,最多由 个小立方块搭成.(3)当d=e=1,f=2时,请在网格中画出这个几何体的左视图.解析 (1)a=3,b=1.(2)这个几何体最少由4+2+3=9个小立方块搭成.这个几何体最多由6+2+3=11个小立方块搭成.(3)如图所示: 21.(2023四川简阳期中)(9分)下图是某几何体的三视图.(1)这个几何体的名称是 .(2)根据图中数据,求出这个几何体所有棱的长度之和以及表 面积. 解析 (1)三棱柱.(2)这个几何体所有棱的长度之和=9×3+2×(3+4+5)=51(cm).结合三视图可知,这个几何体的底面三角形的三边长分别为 3 cm,4 cm,5 cm,∵32+42=52,∴该三角形为直角三角形,∴这个 几何体的表面积=2× ×3×4+9×(3+4+5)=120(cm2).22.(10分)如图所示,在某天晚上,身高是1.6 m的王华同学由 路灯AC底部走向路灯BD底部,当他走到点P时,发现他身后 的影子的顶部刚好接触到路灯AC的底部;当他再向前步行12 m到达点Q时,发现他身前的影子的顶部刚好接触到路灯BD 的底部.已知两个路灯的高度都是9.6 m.(1)求两个路灯之间的距离.(2)当王华走到路灯BD的底部时,他在路灯AC照射下的影长 是多少?解析 (1)由题意可知点D,M,A和C,N,B分别共线,如图,连接 DA和CB,则点M在线段AD上,点N在线段BC上.易证△ABD≌△BAC,△MAP≌△NBQ,∴AP=BQ.∵NQ∥CA,∴Rt△BNQ∽Rt△BCA.∴ = ,即 = ,解得BQ=3 m.∴AB=12+6=18(m).故这两个路灯之间的距离为18 m. (2)如图,设王华走到路灯BD的底部时,他在路灯AC照射下的 影长BE为x m.由题意可知Rt△EFB∽Rt△ECA.∴ = ,即 = ,解得x=3.6.故他在路灯AC照射下的影长为3.6 m.
第五章 素养综合检测(满分100分, 限时90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.(情境题·中华优秀传统文化)(2024广东清远期末)日晷是我 国古代利用日影测定时刻的一种计时仪器,它由“晷面”和 “晷针”组成.当太阳光照在日晷上时,晷针的影子就会投向 晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以 此来显示时刻.晷针在晷面上形成的投影是( )A.中心投影BB.平行投影C.既是平行投影又是中心投影D.不能确定解析 晷针在晷面上形成的投影是由太阳光线照射形成的, 故形成的投影是平行投影.2.(2024河南郑州期末)下图是我们生活中常用的“空心卷 纸”,其主视图(不考虑尺寸)为 ( ) C解析 观察图形可知,该几何体的主视图如图: 故选C.3.(2024四川渠县期末)由5个大小相同的小正方体搭成的几 何体如图所示,关于它的视图,下列说法正确的是 ( ) A.主视图的面积最小B.左视图的面积最小C.俯视图的面积最小D.从三个方向看的视图面积相等C解析 由题意可知,主视图有5个小正方形,俯视图有3个小正 方形,左视图有5个小正方形,所以俯视图的面积最小.4.(2024吉林白山临江期末)若在同一盏路灯下,小明与小强 的影子一样长,则下列说法正确的是 ( )A.小明比小强的个子高B.小强比小明的个子高C.两个人的个子一样高D.无法判断谁的个子高D解析 因为小明与小强所处的位置不确定,所以无法判断谁 的个子高.故选D.5.(2024广西凤山期末)下列立体图形中,主视图和左视图均 为三角形的是 ( ) C解析 A.主视图为矩形,左视图为矩形,故本选项不合题 意;B.主视图为矩形,左视图为矩形,故本选项不合题意;C.主 视图和左视图均为三角形,故本选项符合题意;D.主视图为一 个矩形,矩形中间有一条竖直的实线,左视图为矩形,故本选 项不合题意.故选C.6.(情境题·中华优秀传统文化)(2023山东潍坊中考)在我国古 代建筑中经常使用榫卯构件,如图所示的是某种榫卯构件的 示意图,其中卯的俯视图是 ( ) C解析 由题图可知俯视图为 .故选C.7.(新考法)(2023内蒙古包头期末)如图,通过两人的对话,我们 可以判断他们共同搭的几何体是 ( ) D解析 本题从两人对话中给出的信息进行判断,选项A,主视图和左视图不一样,故不符合题意;选项B,只有5个正方体,故不符合题意;选项C,主视图和左视图不一样,故不符合题意;选项D,主视图和左视图一样,且有6个正方体,故符合题意.故选D.8.如图,这个几何体是由5个相同的小立方块搭成的,若移走 一个小立方块,左视图发生了改变,则移走的小立方块是( ) A.① B.② C.③ D.④C解析 移走小立方块③后,左视图由两行变成了一行,发生了 改变.故选C.9.(2024山东泰安新泰期末)一个几何体是由一些大小相同的 小正方体组成的,其俯视图与主视图如图所示,则组成这个几 何体的小正方体最多有 ( )A.9个 B.10个 C.11个 D.12个C解析 结合俯视图和主视图知,这个几何体的底层有5个小 正方体,从下向上数第二层,最多有3个小正方体,第3层最多 有3个小正方体,因此组成这个几何体的小正方体最多有5+3 +3=11(个).故选C.10.(2023重庆南岸期末)下图是一个由铁铸灌成的几何体的 三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积 为 ( )A.12π B.18π C.24π D.78πB解析 由三视图可得,这个几何体是空心圆柱,其高为6,底面 小圆的半径是1,大圆的半径是2,故这个几何体的体积为6×π×22-6×π×12=24π-6π=18π.故选B.二、填空题(本大题共6小题,每小题3分,共18分)11.(情境题·中华优秀传统文化)(2024四川成都期末)早在1 00 0多年前的宋朝,手影就已经作为民间一种有趣的游戏而存 在.诗人释惠明在《手影戏》中写道:“三尺生绡作戏台,全 凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏 全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、 飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于 (填“平行投影”或“中心投影”).中心投影12.某天学校举办了运动会,小红先参加了校运动会女子100 m比赛,过一段时间又参加了女子400 m比赛,比赛都在上午 进行,下图是摄影师在同一位置拍摄小红的两张照片,那么 (填“甲”或“乙”)照片是在小红参加400 m比赛时 拍摄的.乙解析 易知在太阳光下从早晨到中午物体的影长由长变短, ∵比赛都在上午进行,先进行的是100 m比赛,∴影子较长的 甲照片是参加100 m比赛时拍摄的,影子较短的乙照片是参 加400 m比赛时拍摄的.13.如图,正方形ABCD的边长是5 cm,以直线AB为轴,将正方 形旋转一周后,所得几何体的左视图的面积是 . 50 cm2 解析 由题意可得,旋转所得几何体的左视图为矩形,且矩形 的宽为5 cm,长为2×5=10 cm,故所得几何体的左视图的面积 为5×10=50(cm2).故答案为50 cm2.14.如图所示,一长方体木板上有两个空洞,一个是正方形形 状的,一个是圆形形状的,对于图中的4种几何体,你觉得哪一 种作为塞子既可以堵住圆形空洞又可以堵住正方形空洞? (填序号). ②解析 ②中圆柱的俯视图是圆,可以堵住圆形空洞,主视图和 左视图是正方形,可以堵住正方形空洞,故答案为②.15.如图,在一次数学活动课上,张明用17个棱长为1的小正方 体搭成了一个几何体,然后他请王亮用其他同样的小正方体 在旁边再搭一个几何体,使王亮所搭几何体的左视图与张明 所搭几何体的左视图相同,那么王亮至少需要 个小 正方体. 7解析 由题可知,张明所搭几何体的左视图有7个小正方形, 故王亮至少需要7个小正方体,故答案为7.16.(2024重庆南岸期末)如图所示的是一个几何体的三视图, 俯视图为正三角形,则该几何体的侧面积为 . 36解析 由三视图知该几何体是一个三棱柱,且该三棱柱的高 为6,底面是一个高为 的正三角形,易知该三棱柱的底面正三角形的边长为2,∴该几何体的侧面积是(2+2+2)×6=36,故 答案为36.三、解答题(共52分)17.(8分)甲、乙两根木杆在同一时刻的影子如图所示.(1)请在图中画出形成木杆影子的光线,并指出是平行投影还 是中心投影.(2)若是路灯的光线,请找出路灯灯泡的位置.(3)请在图中画出木杆丙的影子.解析 (1)光线如图所示,是中心投影.(2)如图所示,点O所在的位置是路灯灯泡的位置.(3)木杆丙的影子如图所示.18.(2024陕西榆林十中期末)(8分)如图所示的是由6块小正方 体搭成的几何体(主视图已给出). (1)请在方格图中画出该几何体的左视图和俯视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图 和左视图不变,最多可以再添加 块小正方体.解析 (1)该几何体的左视图和俯视图如图: (2)2.19.(新独家原创)(8分)吊脚楼是中国南方多个少数民族的传 统民居,尤其在渝东南、桂北、湘西、鄂西、黔东南等地区 较为常见,有的吊脚楼为三层建筑,除了屋顶盖瓦以外,上上 下下全部用杉木建造.屋柱用大杉木凿眼,柱与柱之间用大小 不一的杉木斜穿直套连在一起,尽管不用一个铁钉也十分坚 固.图①和图②是吊脚楼常用的榫卯结构,请分别画出图①和 图②的三视图. 解析 题图①的三视图如图:题图②的三视图如图: 20.(9分)用小立方块搭一个几何体,它的主视图和俯视图如 图所示,俯视图中小正方形中的字母表示在该位置上小立方 块的个数.(1)a= ,b= .(2)这个几何体最少由 个小立方块搭成,最多由 个小立方块搭成.(3)当d=e=1,f=2时,请在网格中画出这个几何体的左视图.解析 (1)a=3,b=1.(2)这个几何体最少由4+2+3=9个小立方块搭成.这个几何体最多由6+2+3=11个小立方块搭成.(3)如图所示: 21.(2023四川简阳期中)(9分)下图是某几何体的三视图.(1)这个几何体的名称是 .(2)根据图中数据,求出这个几何体所有棱的长度之和以及表 面积. 解析 (1)三棱柱.(2)这个几何体所有棱的长度之和=9×3+2×(3+4+5)=51(cm).结合三视图可知,这个几何体的底面三角形的三边长分别为 3 cm,4 cm,5 cm,∵32+42=52,∴该三角形为直角三角形,∴这个 几何体的表面积=2× ×3×4+9×(3+4+5)=120(cm2).22.(10分)如图所示,在某天晚上,身高是1.6 m的王华同学由 路灯AC底部走向路灯BD底部,当他走到点P时,发现他身后 的影子的顶部刚好接触到路灯AC的底部;当他再向前步行12 m到达点Q时,发现他身前的影子的顶部刚好接触到路灯BD 的底部.已知两个路灯的高度都是9.6 m.(1)求两个路灯之间的距离.(2)当王华走到路灯BD的底部时,他在路灯AC照射下的影长 是多少?解析 (1)由题意可知点D,M,A和C,N,B分别共线,如图,连接 DA和CB,则点M在线段AD上,点N在线段BC上.易证△ABD≌△BAC,△MAP≌△NBQ,∴AP=BQ.∵NQ∥CA,∴Rt△BNQ∽Rt△BCA.∴ = ,即 = ,解得BQ=3 m.∴AB=12+6=18(m).故这两个路灯之间的距离为18 m. (2)如图,设王华走到路灯BD的底部时,他在路灯AC照射下的 影长BE为x m.由题意可知Rt△EFB∽Rt△ECA.∴ = ,即 = ,解得x=3.6.故他在路灯AC照射下的影长为3.6 m.
相关资料
更多









