




数学3 反比例函数的应用集体备课课件ppt
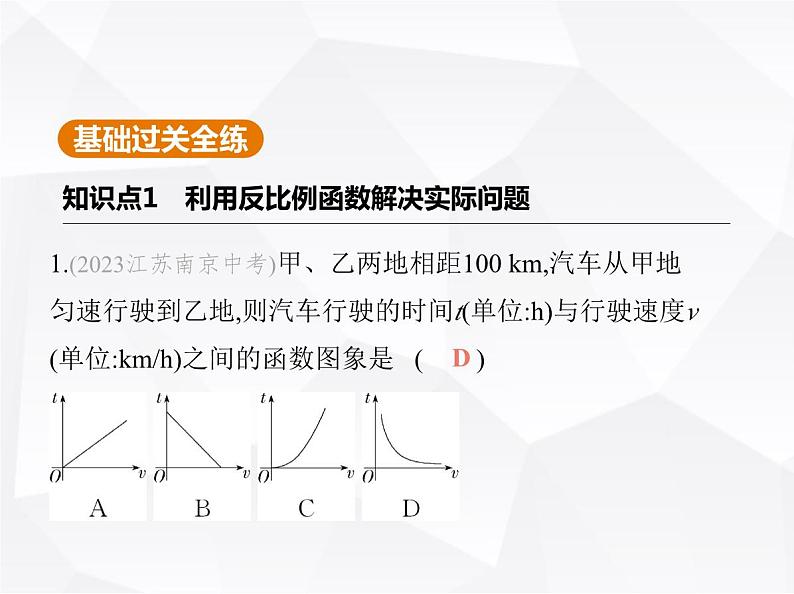
展开1.(2023江苏南京中考)甲、乙两地相距100 km,汽车从甲地 匀速行驶到乙地,则汽车行驶的时间t(单位:h)与行驶速度v (单位:km/h)之间的函数图象是 ( )
解析 根据题意有100=v·t,所以t= ,是反比例函数,其图象在第一象限.故选D.
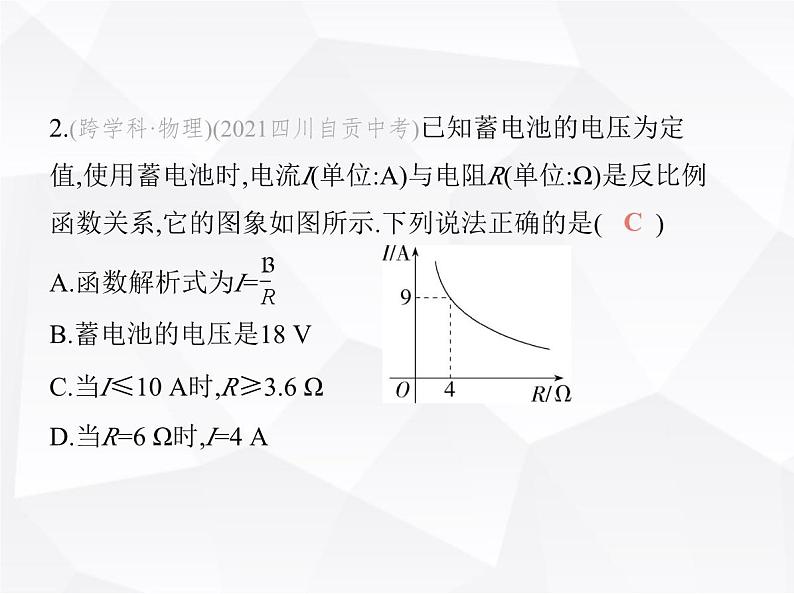
2.(跨学科·物理)(2021四川自贡中考)已知蓄电池的电压为定 值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例 函数关系,它的图象如图所示.下列说法正确的是( )A.函数解析式为I= B.蓄电池的电压是18 V
C.当I≤10 A时,R≥3.6 ΩD.当R=6 Ω时,I=4 A
解析 设I= ,∵图象过点(4,9),∴k=36,∴I= ,∴蓄电池的电压是36 V.∴A,B中说法均错误;当I=10 A时,R=3.6 Ω,由图 象知:当I≤10 A时,R≥3.6 Ω,∴C中说法正确,符合题意;当R=6 Ω时,I=6 A,∴D中说法错误.故选C.
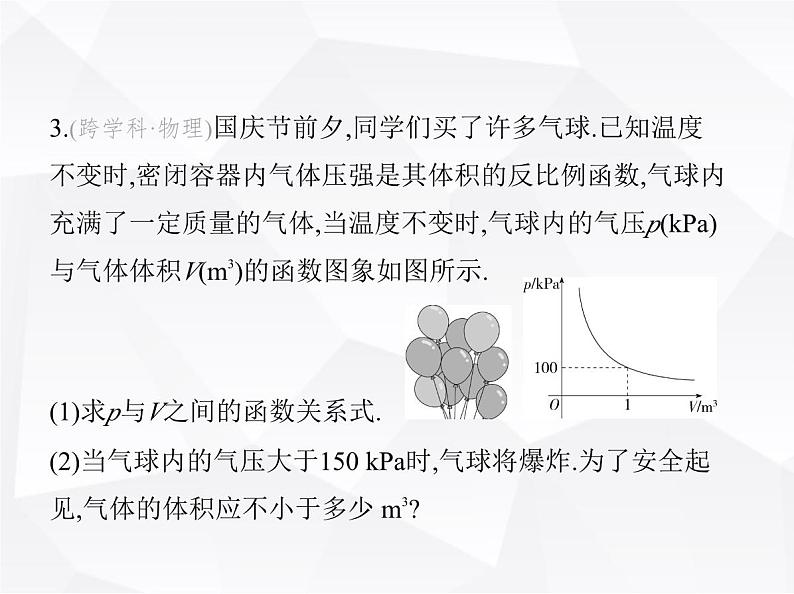
3.(跨学科·物理)国庆节前夕,同学们买了许多气球.已知温度 不变时,密闭容器内气体压强是其体积的反比例函数,气球内 充满了一定质量的气体,当温度不变时,气球内的气压p(kPa) 与气体体积V(m3)的函数图象如图所示.
(1)求p与V之间的函数关系式.(2)当气球内的气压大于150 kPa时,气球将爆炸.为了安全起 见,气体的体积应不小于多少 m3?
解析 (1)设气球内气体的气压p(kPa)和气体体积V(m3)的关 系式为p= ,∵图象过点(1,100),∴k=100,∴p与V之间的函数关系式为p= .(2)在第一象限内,p随V的增大而减小,当p=150 kPa时,V= = = m3.∴为了安全起见,气球的体积应不小于 m3.
4.在某河治理工程施工过程中,某工程队接受一项开挖水渠 的工程,所需天数y与每天完成的工程量x(m)的函数关系图象 如图所示.(1)请根据题意,求y与x之间的函数表达式.(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠15 m,则该工程队需用多少天才能完成此项任务?(3)为了防汛工作的需要,必须在一个月内(按30天计算)完成 任务,那么每天至少要完成多少米?
解析 (1)设y= .∵点(24,50)在其函数图象上,∴k=24×50=1 200,∴所求函数表达式为y= .(2)由图象可知共需开挖水渠24×50=1 200(m),2台挖掘机需要工作1 200÷(2×15)=40(天).(3)当y=30时,30= ,∴x=40,故每天至少要完成40 m.
5.(情境题·双减)(2024广西北海期末)很多学生由于学习时间 过长,用眼不科学,视力下降,国家“双减”政策的目标之一 就是减轻学生过重的作业负担,让学生提质增效.近视眼镜可 以清晰看到远距离物体,它的镜片是凹透镜,研究发现,近视 眼镜的度数y(度)与镜片焦距x(m)的关系式为y= .(1)当镜片焦距是0.1 m时,近视眼镜的度数是多少?(2)当近视眼镜的度数是400度时,镜片焦距是多少?(3)小明原来佩戴300度的近视眼镜,经过一段时间的矫正治
疗并注意用眼健康,复查验光时,所配镜片焦距调整为0.5 m, 则小明的眼镜度数下降了多少?
(2)当y=400时,x= =0.25.答:当近视眼镜的度数是400度时,镜片焦距是0.25 m.(3)当x=0.5时,y= =200,
300-200=100(度).答:小明的眼镜度数下降了100度.
6.(2023内蒙古呼伦贝尔中考)如图,直线y=ax+b(a≠0)与双曲 线y= (k≠0)交于点A(-2,4)和点B(m,-2),则不等式0
解析 观察题中图象,可知直线y=ax+b在x轴上方且在双曲线y= 下方的部分的横坐标满足-2
解析 在y=x+4中,令x=0,则y=4,∴A(0,4),即OA=4,∵AO=4BO,∴BO=1.在y=x+4中,令x=1,则y=5,∴C(1,5),∵点C(1,5)在反比例函数y= 的图象上,∴k=5.
8.(2024河南安阳期末)如图,一次函数y=x+1与反比例函数y= 的图象相交于A(m,2),B两点,连接OA,OB.(1)求这个反比例函数的表达式.(2)求△AOB的面积.
解析 (1)∵一次函数y=x+1的图象经过点A(m,2),∴m+1=2, ∴m=1,∴A(1,2),∵反比例函数y= 的图象经过点A(1,2),∴2= ,∴k=2,∴反比例函数的解析式为y= .(2)由题意,得
解得 或 ∴B(-2,-1),当x=0时,y=x+1=1,∴C(0,1),∴OC=1,∴S△AOB=S△BOC+S△AOC= ×1×2+ ×1×1=1.5.
9.(2022山东淄博中考)如图,直线y=kx+b与双曲线y= 相交于A(1,2),B两点,与x轴相交于点C(4,0).(1)分别求直线AC和双曲线对应的函数表达式.(2)连接OA,OB,求△AOB的面积.(3)直接写出当x>0时,关于x的不等式kx+b> 的解集.
解析 (1)将A(1,2),C(4,0)代入y=kx+b,得 解得 ∴直线AC的函数表达式为y=- x+ .将A(1,2)代入y= ,得m=2,∴双曲线的函数表达式为y= .
(2)联立 解得 或 ∴点B的坐标为 .∴S△AOB=S△AOC-S△BOC= ×4×2- ×4× = .(3)由题中图象知,当1
A.该段航行过程中,F随v的增大而减小B.F>10 N时,v>2 m·s-1C.该段航行过程中,函数表达式为F=
D.v=8 m·s-1时,F=2.5 N
解析 A.根据图象可知,F·v是定值,F随v的增大而减小,说法 正确,不符合题意;B.当F>10 N时,v<2 m·s-1,说法错误,符合题意;C.根据图象信息,易知函数表达式为F= ,说法正确,不符合题意;D.当v=8 m·s-1时,F= =2.5 N,说法正确,不符合题意.故选B.
11.(2024辽宁盘锦期末,19,★★☆)如图,在平面直角坐标系 中,直线l:y=mx+n(m≠0)与反比例函数y= (k≠0)的图象交于A(1,a),B(-3,-2)两点,直线l与x轴交于点M.(1)求一次函数和反比例函数的表达式.(2)将直线l向下平移8个单位长度后,与x轴交于点C,连接CA, CB,求△ABC的面积.(3)请结合图象,直接写出不等式mx+n≥ 的解集.
解析 (1)将点B的坐标代入反比例函数表达式得k=-2×(-3)= 6,则反比例函数表达式为y= ,∵A在反比例函数图象上,∴a= =6,∴点A(1,6),将点A、B的坐标代入y=mx+n,得 解得 ∴一次函数的表达式为y=2x+4.(2)易知M(-2,0),平移后的直线对应的函数表达式为y=2x+4-8 =2x-4,当y=2x-4=0时,x=2,
∴C(2,0),则CM=4,则△ABC的面积=S△CMA+S△CMB= ×CM×(yA-yB)= ×4×(6+2)=16.(3)x≥1或-3≤x<0.
12.(情境题·社会热点)(2024陕西子洲期末,24,★★☆)实验数 据显示,一般情况下,成人喝0.25 kg低度白酒后,1.5小时内其 血液中酒精含量y(毫克/百毫升)与时间x(小时)成正比例关 系;1.5小时后(包括1.5小时)y与x成反比例关系.根据图中提供 的信息,解答下列问题:(1)写出一般情况下,成人喝0.25 kg低度白酒后,y与x之间的函 数关系式及相应的自变量取值范围.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于 20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上
述数学模型,假设某驾驶员晚上在家喝完0.25 kg低度白酒,则 10小时后该驾驶员能否驾车去上班?请说明理由.
解析 (1)当0≤x<1.5时,设函数关系式为y=kx,易知点(1.5,150)在该函数图象上,则150=1.5k,解得k=100,故y=100x(0≤x<1.5).当x≥1.5时,设函数关系式为y= ,则a=150×1.5=225,故y= (x≥1.5).综上所述,y与x之间的函数关系式为y= (2)10小时后该驾驶员不能驾车去上班.
理由:当x=10时,y= =22.5,∵22.5>20,∴10小时后该驾驶员不能驾车去上班.
13.(跨学科·物理)(2024河北迁安期末,23,★★☆)如图1,琪琪 同学设计了一个探究杠杆平衡条件的实验,在一个自制类似 天平的仪器左边的固定托盘A中放置一个重物,在右边的活 动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右 平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中 砝码的质量y(g)的变化情况.嘉嘉将实验数据记录在下表中.
(1)在记录的过程中,一个数据被墨汁覆盖,则被覆盖的数值 应为 .(2)依据表格数据,在图2中描出相应的点,并用平滑曲线连接, 观察所画的图象,猜测y与x之间的函数关系类型,求出函数关 系式并加以验证.
(3)当砝码的质量为40 g时,为了使仪器左右平衡,活动托盘B 与点O的距离应是多少 cm?
解析 (1)由题表可知,活动托盘B与点O的距离x(cm)与活动 托盘B中砝码的质量y(g)的乘积为定值60,∴被覆盖的数值应为60÷10=6,故答案为6.(2)画出函数图象如图所示: 猜测y与x的函数关系为反比例函数.
设y= (k≠0),把(5,12)代入得12= ,解得k=60,∴y= ,将其余各点坐标代入验证,均满足函数关系式,∴y与x之间的函数关系式为y= .(3)把y=40代入y= 得40= ,解得x=1.5,当砝码的质量为40 g时,活动托盘B与点O的距离是1.5 cm.
14.(模型观念)探究:是否存在一个新矩形,使其周长和面积为 原矩形的2倍、 、k倍?(1)若该矩形为正方形,是否存在一个正方形,使其周长和面 积都为边长为2的正方形的2倍? (填“存在”或 “不存在”).(2)继续探究,是否存在一个矩形,使其周长和面积都为长为3, 宽为2的矩形的2倍?
①设新矩形的长和宽分别为x、y,则依题意得x+y=10,xy=12, 联立 得x2-10x+12=0,再探究根的情况.根据此方法,请你探究是否存在一个矩形,使其周长和面积都 为原矩形的 .②如图,也可用反比例函数与一次函数证明:已知l1:y=-x+10,l2:y= .
a.是否存在一个新矩形为原矩形周长和面积的2倍? (填“存在”或“不存在”).
b.请探究是否有一新矩形的周长和面积为原矩形的 ,若不存在,用图象表达.c.请写出当“存在新矩形的周长和面积均为原矩形的k倍” 时,k的取值范围: .
解析 (1)由题意得,原正方形的周长为8,面积为4,若存在新 正方形满足条件,则新正方形的周长为16,面积为8,对应的边 长分别为4和2 ,不符合题意,∴不存在新正方形的周长和面积是边长为2的正方形的2倍. 故答案为不存在.(2)①设新矩形的长和宽分别为x、y,则依题意得x+y=2.5,xy= 3,联立 得2x2-5x+6=0,∵Δ=(-5)2-4×2×6=-23<0,
∴此方程无解,∴不存在新矩形使其周长和面积都为原矩形的 .②a.从图象来看,函数y=-x+10和函数y= 的图象在第一象限有两个交点,∴存在新矩形,使其周长和面积都是原矩形的2倍.故答案为存在.b.如图,从图象来看,函数y=-x+2.5和函数y= 的图象在第一象限没有交点,
∴不存在新矩形,使其周长和面积是原矩形的 . c.设新矩形的长和宽分别为x、y,则依题意得x+y=5k,xy=6k,联立 得x2-5kx+6k=0,
数学九年级上册3 反比例函数的应用评课ppt课件: 这是一份数学九年级上册<a href="/sx/tb_c99915_t3/?tag_id=26" target="_blank">3 反比例函数的应用评课ppt课件</a>,共14页。PPT课件主要包含了一个分支,其中一部分,-1x0或x2等内容,欢迎下载使用。
初中数学北师大版九年级上册第六章 反比例函数3 反比例函数的应用教学课件ppt: 这是一份初中数学北师大版九年级上册第六章 反比例函数3 反比例函数的应用教学课件ppt,共14页。PPT课件主要包含了反比例函数的定义,复习回顾,增减性,一三象限,y随x的增大而增大,y随x的增大而减小,二四象限,归纳小结等内容,欢迎下载使用。
数学九年级上册3 反比例函数的应用课前预习ppt课件: 这是一份数学九年级上册3 反比例函数的应用课前预习ppt课件,共6页。PPT课件主要包含了A94等内容,欢迎下载使用。













