2025年高考一轮复习系列（新高考新题型）3.2利用导数研究函数的单调性-1含解析答案

这是一份2025年高考一轮复习系列（新高考新题型）3.2利用导数研究函数的单调性-1含解析答案，共28页。试卷主要包含了2 利用导数研究函数的单调性等内容，欢迎下载使用。

考点一 函数与导函数图像的关系
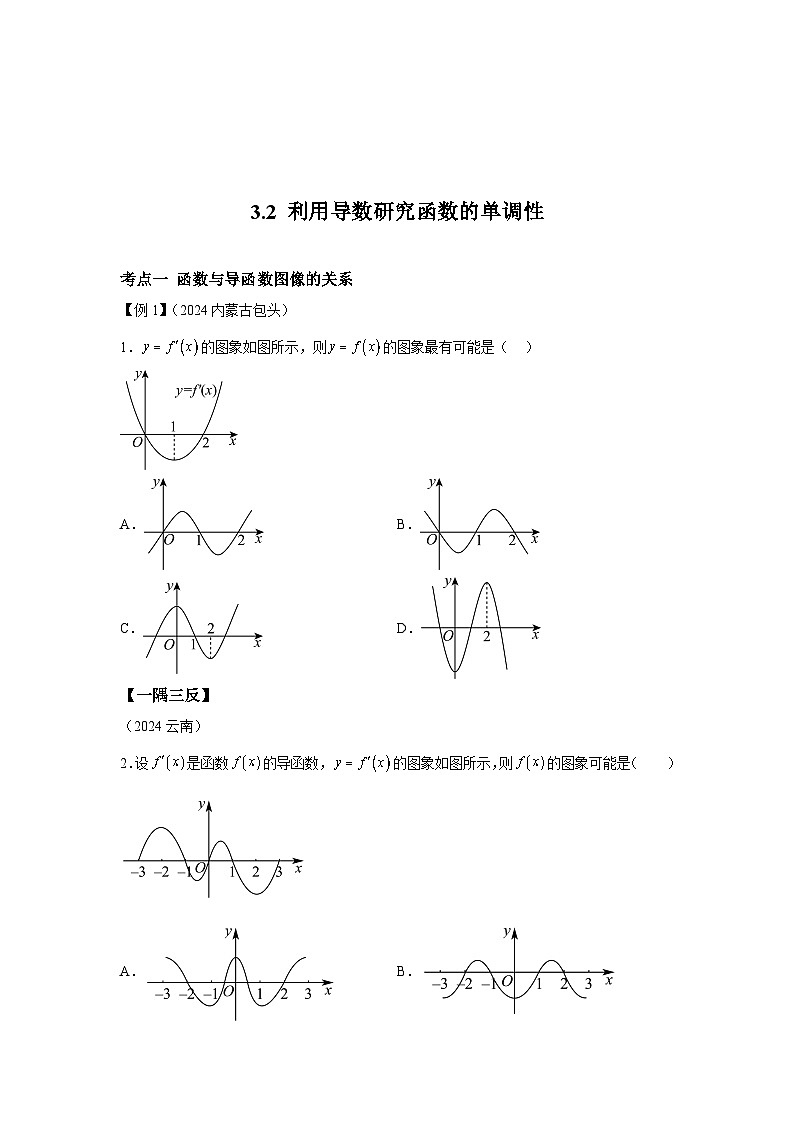
【例1】（2024内蒙古包头）
1．的图象如图所示，则的图象最有可能是（ ）

A． B．
C． D．
【一隅三反】
（2024云南）
2．设是函数的导函数，的图象如图所示，则的图象可能是（ ）

A． B．
C． D．
（2023·浙江绍兴·模拟预测）
3．如图是函数的导函数的图象，若，则的图象大致为（ ）
A．B．
C．D．
（2024·黑龙江齐齐哈尔）
4．已知函数的图象如图所示（其中是函数的导函数），下面四个图象中可能是图象的是（ ）
A．B．
C．D．
考点二 无参函数单调区间
【例2】（2024广东东莞）
5．函数的单调递增区间是（ ）
A．B．
C．D．
（2024重庆·阶段练习）
6．函数的单调递增区间为（ ）
A．B．C．D．
（2024北京）
7．已知函数，则的单调递增区间为（ ）
A．B．C．D．
【一隅三反】
（2024广东东莞）
8．函数的单调减区间为（ ）
A．B．C．D．
（2024重庆长寿）
9．函数的单调递减区间为（ ）
A．（0，2）B．（2，3）
C．（1，3）D．（3，+∞）
（2024·浙江·模拟预测）
10．函数的单调递增区间是（ ）
A．B．
C．D．
考点三 某区间上单调求参
【例3-1】（2024江西南昌）
11．已知函数在区间上单调递减，则实数m的取值范围是（ ）
A．B．C．D．
【例3-2】（2024江苏南京）
12．已知函数在区间上单调递增，则实数a的最小值为（ ）
A．0B．1C．2D．3
【例3-3】（2024海南海口）
13．已知函数在上为减函数，则的取值范围是（ ）
A．B．C．D．
【例3-4】（2024浙江）
14．已知函数在区间上是减函数，则实数的取值范围为（ ）
A．B．C．D．
【一隅三反】
（2024·广东茂名·一模）
15．若是区间上的单调函数，则实数的值可以是（ ）
A．B．C．3D．4
（2024福建南平）
16．已知函数在区间上单调递减，则实数的取值范围为（ ）
A．B．C．D．
（2023高三·全国·专题练习）
17．已知函数的单调递减区间为，则（ ）.
A．B．
C．D．
（2024安徽宿州）
18．已知函数在区间上单调递增，则实数的取值范围是（ ）
A．B．
C．D．
考点四 某区间存在单调求参
【例4-1】（2024福建泉州·阶段练习）
19．若函数在上存在单调递增区间，则实数的取值范围为（ ）
A．B．C．D．
【例4-2】（2024·内蒙古呼和浩特·一模）
20．在区间上，函数存在单调递增区间，则实数的取值范围是（ ）
A．B．
C．D．
【一隅三反】
（2024内蒙古锡林郭勒盟·期末）
21．若函数在上存在单调递减区间，则的取值范围是（ ）
A．B．
C．D．
（2024重庆江北·期中）
22．若函数在区间内存在单调递减区间，则实数的取值范围是（ ）
A．B．
C．D．
（2024江西萍乡）
23．已知函数在区间上存在单调递增区间，则实数的取值范围是（ ）
A．B．
C．D．
（2024江苏常州）
24．若函数存在单调递减区间，则实数的取值范围为是 .
考点五 某区间上不单调求参
【例5-1】（23-24高三上·福建三明·期中）
25．已知函数，则在上不单调的一个充分不必要条件是（ ）
A．B．C．D．
【例5-2】（2024江苏苏州·期末）
26．若函数在区间上不单调，则实数的值可能是（ ）
A．2B．3C．D．4
【一隅三反】
（2024四川绵阳）
27．已知函数，则在上不单调的一个充分不必要条件是（ ）
A．B．
C．D．
（2024山东德州）
28．若函数在(0，1)上不单调，则的取值范围是（ ）
A．B．
C．D．
（2024北京）
29．已知函数．若在内不单调，则实数a的取值范围是 ．
考点六 含参函数的单调性分类讨论
【例6-1】（2024·福建漳州·一模）
30．已知函数，且．
(1)证明：曲线在点处的切线方程过坐标原点．
(2)讨论函数的单调性．
【例6-2】（2024高三·全国·专题练习）
31．已知函数，讨论的单调性.
【例6-3】
（2024高三·全国·专题练习）
32．已知，讨论的单调性.
【一隅三反】
（2024浙江杭州·期末）
33．已知函数.
(1)讨论的单调性；
(2)已知时，直线为曲线的切线，求实数的值．
（2024安徽）
34．已知函数.
(1)若，求曲线在点处的切线；
(2)讨论的单调性；
（2024高三·全国·专题练习）
35．已知函数．，讨论函数的单调区间；
（2024湖南）
36．已知，讨论函数的单调性.
（2024广东湛江）
37．设函数（），讨论的单调性.
考点七 单调性的应用之比较大小
【例6-1】（2024·云南贵州·二模）
38．已知，则的大关系为（ ）
A．B．
C．D．
【一隅三反】
（2024·全国·模拟预测）
39．若，则（ ）
A．B．C．D．
（2024·四川成都·模拟预测）
40．已知函数，若，，，则（ ）
A．B．
C．D．
（2024·全国·模拟预测）
41．若，，，则，，的大小顺序为（ ）
A．B．C．D．
参考答案：
1．C
【分析】利用导数与函数单调性的关系可得出合适的选项.
【详解】由导函数的图象可知，当或时，；当时，.
所以，函数的增区间为和，减区间为，
所以，函数的图象为C选项中的图象.
故选：C.
2．D
【分析】解法一：根据导函数的正负，得到的单调性，即可判断；
解法二：由导函数的图象可知在处取得极大值，即可判断.
【详解】解法一：因为在和上，在和上，
所以函数在，上单调递增，在，上单调递减，
观察各选项知，只有D符合题意.
解法二：由题图知，在的左侧大于、右侧小于，
所以函数在处取得极大值，观察各选项知，只有D符合题意.
故选：D.
3．D
【分析】根据导函数的图象在区间内的函数的范围，判断出函数区间上各点处切线的斜率的范围，根据导函数的图象得导函数函数值的符号，得函数的单调性，再结合四个选项可得答案.
【详解】由的图象可知，当时，，则在区间上，函数上各点处切线的斜率在区间内，
对于A，在区间上，函数上各点处切线的斜率均小于0，故A不正确；
对于B，在区间上，函数上存在点，在该点处切线的斜率大于1，故B不正确；
对于C，在区间上，函数上存在点，在该点处切线的斜率大于1，故C不正确；
对于D，由的图象可知，当时，，当时，，当时，，
所以函数上各点处切线的斜率在区间内，在上单调递增，在上单调递减，在上单调递增，
而函数的图象均符合这些性质，故D正确.
故选：D
4．C
【分析】根据的图像，得到不同范围下，的正负，得到的单调性，得到答案.
【详解】由的图象知，当时，，故，单调递增；
当时，，故，当，，故，
等号仅有可能在x＝0处取得，
所以时，单调递减；
当时，，故，单调递增，结合选项只有C符合.
故选：C.
5．D
【分析】利用导数求函数的单调区间.
【详解】的定义域为，
，
令，可得，解得：.
故函数的单调递增区间是.
故选：D.
6．C
【分析】求出函数导数，令可得解.
【详解】因为，
所以令可得，解得，
所以函数的单调递增区间为.
故选：C
7．A
【分析】根据对数真数大于零可构造不等式组求得函数定义域；利用导数可求得函数单调递增区间．
【详解】由得：，即的定义域为；
因为，
所以当时，；当时，；
所以的单调递增区间为．
故选：A.
8．A
【分析】求出函数导数，由得解.
【详解】，
令可得，即，
所以当时，函数单调递减.
故选：A
9．B
【分析】对求导，令求出的范围，即可得出答案.
【详解】的定义域为,
,
令，解得：.
所以函数的单调递减区间为（2，3）.
故选：B.
10．D
【分析】求出函数的定义域与导函数，再令，解得即可.
【详解】函数的定义域为，
且，
令，解得，
所以的单调递增区间为.
故选：D
11．B
【分析】求导可得的单调减区间，根据题意，可得，列出不等式，即可求得答案.
【详解】由题意得，
令，可得，
因为在区间上单调递减，所以，
所以，解得．
故选：B．
12．B
【分析】根据题意，恒成立，分离参数结合二次函数的性质求得答案.
【详解】因为函数在上单调递增，所以对恒成立，
即恒成立，设，，
当时，，所以，则，
所以实数a的最小值为.
故选：B.
13．D
【分析】由题意可得在上恒成立，即在上恒成立，令，求出取值范围即可.
【详解】因为函数在上为减函数，
所以在上恒成立，
所以在上恒成立，令，
所以，
所以在上单调递减，所以，
故，所以的取值范围是.
故选：D.
14．B
【分析】根据函数的单调性知导数小于等于0恒成立，分离参数后由正切函数单调性求解.
【详解】由题意，在上恒成立，
即在上恒成立，
因为在上单调递增，所以，
所以在时，，
所以.
故选：B
15．CD
【分析】求导，分析导函数的正负得到原函数的单调性，再由已知建立关于的不等式组，解出即可．
【详解】由题意，，
令，解得，令，解得或，
所以在上单调递减，在，上单调递减，
若函数在区间上单调，
则或或，解得或或，
即或.
故选：CD.
16．A
【分析】利用导数与函数的关系将问题转化为恒成立问题，从而得解.
【详解】因为，所以，
因为在区间上单调递减，
所以，即，则在上恒成立，
因为在上单调递减，所以，故.
故选：A.
17．B
【分析】根据得到，再根据的单调递减区间是，得到和1是方程的两个根，代入解方程即可.
【详解】由得，又的单调递减区间是，所以和1是方程的两个根，代入得.经检验满足题意
故选：B.
18．C
【分析】求得，由题意转化为在上恒成立，设，求得，令，利用导数求得单调递增，结合，得到在上单调递减，利用，即可求解.
【详解】由函数，可得，
因为函数在区间上单调递增，可得在上恒成立，
即在上恒成立，
设，可得，
令，可得
当时，，所以单调递增，
又因为，
所以，所以在上单调递减，
所以，即实数的取值范围是.
故选：C.
【点睛】方法技巧：对于利用导数研究不等式的恒成立与有解问题的求解策略：
1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；
2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．
3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．
19．D
【分析】根据条件得出存在，使成立，即存在，使成立，构造函数，，求出的最值即可解决问题.
【详解】因为函数在上存在单调递增区间，
所以存在，使成立，即存在，使成立，
令，， 变形得，因为，所以，
所以当，即时，，所以，
故选：D．
20．C
【分析】根据给定条件，利用导数结合函数单调性建立不等式，再构造函数求出函数最大值即得.
【详解】函数，求导得，
依题意，不等式在上有解，即在上有解，
令，，求导得，
当时，，函数单调递增，当时，，函数单调递减，
当时，，因此，
所以实数的取值范围是.
故选：C
21．D
【分析】求出函数的导数，利用导函数小于0在上有解求解即得.
【详解】函数，求导得，
由函数在上存在单调递减区间，得在上有解，
即不等式在上有解，
而函数在上单调递减，当时，，则，
所以的取值范围是.
故选：D
【点睛】结论点睛：若函数在区间上存在单调递增区间，则，使得成立；若函数在区间上存在单调递减区间，则，使得成立.
22．A
【分析】由题意可知：存在，使得，利用参变分离结合存在性问题分析求解.
【详解】因为，
由题意可知：存在，使得，整理得，
且在上单调递减，则，可得，
所以实数的取值范围是.
故选：A.
23．B
【分析】分析可知，存在，使得，由参变量分离法可得，求出函数在上的最小值，即可得出实数的取值范围.
【详解】因为，则，
因为函数在区间上存在单调递增区间，则存在，使得，
即，可得，设，
因为函数、在上均为增函数，则函数在上为增函数，
当时，，故.
故选：B.
24．
【分析】求导后结合二次函数的性质分析即可.
【详解】，
因为函数存在单调递减区间，
所以存在，使得小于零，
所以导函数的判别式，解得或，
所以实数的取值范围为是，
故答案为：.
25．B
【分析】求导，令，根据在上不单调，由在上有变号零点求解.
【详解】，
令，
因为在上不单调，
在上有变号零点，即在上有变号零点，
当 时， ，不成立；
当 时，只需 ，即 ，
解得 或 ，
所以 在上不单调的充要条件是或 ，
所以在上不单调的一个充分不必要条件是，
故选：B
26．BC
【分析】利用导函数判断的单调区间进行求解即可.
【详解】的定义域为，所以，A错误；
由题意可得，令解得，
所以当时，，单调递减，
当时，，单调递增，
因为在区间上不单调，所以，即，
选项B：当时，，正确；
选项C：当时，，
所以，正确；
选项D：当时，，错误；
故选：BC
27．C
【分析】先求出函数的导数，再根据在上不单调可得在上有零点，且在该零点的两侧附近函数值异号，就和分类讨论后可得实数的取值范围，从而可得正确的选项.
【详解】，
若在上不单调，令，
对称轴方程为，则函数与
轴在上有交点．当时，显然不成立；
当时，有解得或．
四个选项中的范围，只有为的真子集，
∴在上不单调的一个充分不必要条件是.
故选：C．
28．A
【分析】求导得，原问题可转化为在上有变号零点，由于单调递增，只需满足，解之即可．
【详解】解：，，
若在上不单调，则在上有变号零点，
又单调递增，，即，解得．
的取值范围是．
故选：．
【点睛】本题考查利用导数研究函数的单调性、零点存在定理，理解原函数的单调性与导函数的正负性之间的联系是解题的关键，考查学生的逻辑推理能力和运算能力，属于中档题．
29．
【分析】求出函数的导数，然后参数分离，先求出函数在内单调时的范围，从而可得不单调时的范围.
【详解】由，得，
当在内为减函数时，则在内恒成立，
所以在内恒成立，
当在内为增函数时，则在内恒成立，
所以在内恒成立，
令，因为在内单调递增，在内单调递减，
所以在内的值域为，所以或，
所以函数在内单调时，a的取值范围是，
故在上不单调时，实数a的取值范围是．
故答案为：．
30．(1)证明见解析
(2)答案见解析
【分析】（1）先利用导数的几何意义求得在处的切线方程，从而得证；
（2）分类讨论与，利用导数与函数的单调性即可得解.
【详解】（1）因为，所以，
则，，
所以在处的切线方程为:，
当时，，故，
所以曲线在点处切线的方程过坐标原点.
（2）由（1）得，
当时，，则，故单调递减；
当时，令则，
当时，，单调递增；
当时，，单调递减；
综上：当时，在上单调递减；
当时，在上单调递增，在上单调递减.
31．答案见解析
【分析】求导得，分、、、讨论可得答案.
【详解】函数的定义域为，
求导得，
①当，即时，由，得，由，得，
因此在上单调递增，在上单调递减；
②当，即时，由，得或，由，得，
因此在，上单调递增，在上单调递减；
③当，即时，恒成立，因此在上单调递增；
④当，即时，由，得或，由，
得，
因此在，上单调递增，在上单调递减，
综上所述，当时，在上单调递减，在上单调递增；
当时，在，上单调递增，在上单调递减；
当时，在上单调递增；
当时，在，上单调递增，在上单调递减．
32．当时，在R上单调递增；当或时，在，上单调递增，在上单调递减．
【分析】通过求出函数的导数，对其导数进行正负判断，进而求出单调区间.
【详解】由题得，令得，
①若，即当时，恒成立，在R上单调递增；
②若，即当或时，可得的两根分别为，，
当时，，当时，，
所以在，上单调递增，在上单调递减．
综上，当时，在R上单增；
当或时，在，上单调递增，在上单调递减．
33．(1)答案见解析
(2)或
【分析】（1）求导后因式分解，再讨论当，，时导函数的正负，即可判断原函数的单调性.
（2）求导后根据导数的几何意义设切点，求得切线方程，根据切线过原点计算即可求得结果.
【详解】（1）．
令，得或．
若，则当时，；当时，．
故在上单调递增，在上单调递减；
若时，，在上单调递增；
若，则当时，；当时，．
故在上单调递增，在上单调递减．
综上所述：当时，在上单调递增，在上单调递减；
当时，在上单调递增；
时，在单调递增，在单调递减．
（2）当时，
设切点，则切线方程为
因为切线过原点， 故， 即，
解得或
所以或.
34．(1)
(2)答案见解析
【分析】（1）求导，利用导数的几何意义得到切线方程；
（2）求导，对导函数因式分解，分，和三种情况，进行求解函数的单调性.
【详解】（1）当时，函数，则，切点坐标为，
，则曲线在点处的切线斜率为，
所求切线方程为，即.
（2），函数定义域为R，
，
①，解得或，解得，
所以在和上单调递增，在上单调递减，
②，解得或，解得，
所以在和上单调递增，在上单调递减，
③，恒成立，在上单调递增.
综上，当时，在和上单调递增，在上单调递减；
当时，在和上单调递增，在上单调递减；
当时，在上单调递增.
35．答案见解析
【分析】求出函数的导数，分和两种情况讨论，当时，继而讨论导函数等于0时两个解的大小关系，判断导数正负，即可求得答案.
【详解】依题意知函数定义域为，
当时，，，
∴当时，，在上单调递增，
当时，，在单调递减；
当时，令，得，，
（i）当，时，即，而，
则时，时，
在，上均为增函数；在上为减函数；
（ii）当，，即时，，
在上为增函数；
(iii)当，，即时，
则时,，时,，
在，上均为增函数；在上为减函数.
综上：当时，增区间为，，减区间为；
当时，增区间为；
当时，增区间为和，减区间为；
当时，增区间为，减区间为.
36．答案见解析
【分析】求出函数的导数，对分类讨论，由导数的正负求出函数的单调区间.
【详解】由题意知，函数的定义域为，且

①当时，因为，所以，所以.
所以当时，，单调递减；当时，，单调递增.
②当时，由，解得；由，解得或.
所以在上单调递减，在，上单调递增.
③当时，（当且仅当时，取等号）恒成立，所以在上单调递增.
④当时，由，解得；由，解得或.
所以在上单调递减，在，上单调递增.
综上，当时，在上单调递减，在上单调递增；
当时，在上单调递减，在，上单调递增；
当时，在上单调递增；
当时，在上单调递减，在，上单调递增.
37．答案见解析
【分析】分类讨论的不同取值，利用导函数的符号判断单调性即可.
【详解】由题意可得的定义域为，，
设，令，，
①当时，，此时恒成立，在上单调递增；
②当时，，设的两根为，
由，可知的两根都小于0，
所以在上大于0，所以在上单调递增；
③当时，，由，解得，，
由，可知的两根都大于0，
所以当时，，，在，上单调递增，
当时，，，在上单调递减.
综述所述：当时，在上单调递增；
当时，在，上单调递增，在上单调递减.
38．B
【分析】根据的特点，构造函数，判断其单调性，得到，故有，再运用作差法比较即得.
【详解】设，则，
当时，，在上递增；
当时，，在上递减,
故.
则，即；
由可知，故.
故选：B.
39．D
【分析】变形后构造函数，求导得到函数单调性，比较出大小
【详解】因为，
所以令，则，
，
当时，，所以函数在上单调递减．
又，所以，即．
故选：D．
40．B
【分析】先利用函数奇偶性的定义与导数判断的奇偶性与单调性，再构造函数，利用导数判断得，从而得解.
【详解】因为的定义域为，
又，
所以是偶函数，
又，
令，则恒成立，
所以当时，，即，
又在上单调递增，所以，
所以在上恒成立，则在上单调递增，
构造函数，则，
令，得，令，得，
所以在上单调递增，在上单调递减，
所以，又，
所以，所以，
所以，所以.
故选：B.
41．B
【分析】结合已知要比较函数值的结构特点，构造函数，利用导数研究函数单调性，通过函数单调性比较大小即可.
【详解】构造函数，则，，，
由，令得，令得，
则在上单调递增，在上单调递减．
因为，所以，所以；
因为，所以，所以；
令，且，则，
令，，
则，
所以在上单调递增，
又，所以，所以，
因为，且，所以，所以.
故选：B