初中数学人教版九年级上册25.3 用频率估计概率评课课件ppt

这是一份初中数学人教版九年级上册25.3 用频率估计概率评课课件ppt，共32页。PPT课件主要包含了学习目标，情境引入，讲授新课，试验探究，试验次数，归纳总结，图钉落地的试验，频率与概率的关系，当堂练习，课堂小结等内容，欢迎下载使用。

1. 理解试验次数较大时试验频率趋于稳定这一规律；(重点)2. 结合具体情境掌握如何用频率估计概率；(重点)3. 通过概率计算进一步比较概率与频率之间的关系．
25.3 用频率估计概率
问题1 抛掷一枚均匀硬币，硬币落地后，会出现哪些可能的结果呢？
问题2 它们的概率是多少呢？
可能出现“正面朝上”或“反面朝上”两种结果
问题3 在实际掷硬币时，会出现什么情况呢？
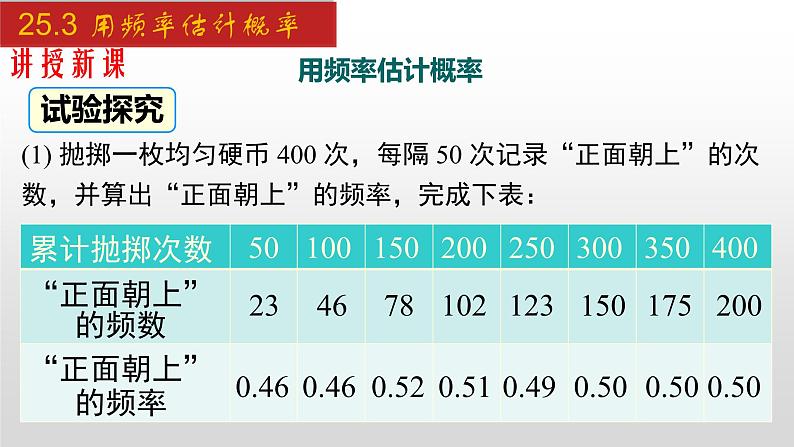
(1) 抛掷一枚均匀硬币 400 次，每隔 50 次记录“正面朝上”的次数，并算出“正面朝上”的频率，完成下表：
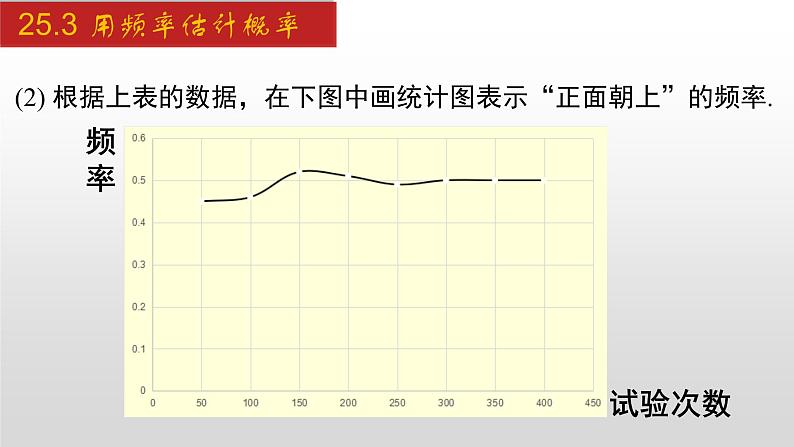
(2) 根据上表的数据，在下图中画统计图表示“正面朝上”的频率.
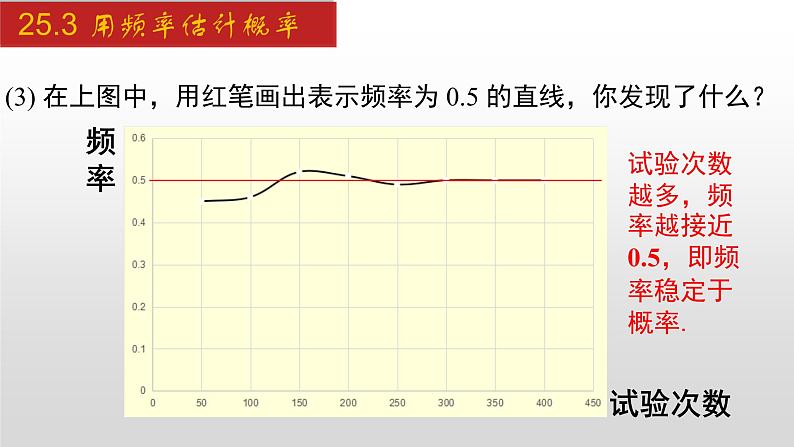
(3) 在上图中，用红笔画出表示频率为 0.5 的直线，你发现了什么？
试验次数越多，频率越接近 0.5，即频率稳定于概率.
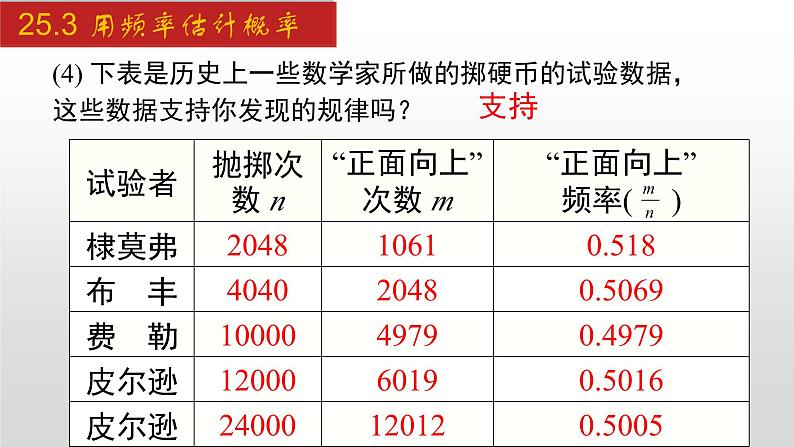
(4) 下表是历史上一些数学家所做的掷硬币的试验数据，这些数据支持你发现的规律吗？
通过大量重复试验，可以用随机事件发生的频率来估计该事件发生的概率.
思考 抛掷硬币试验的特点： 1.可能出现的结果数__________； 2.每种可能结果的可能性__________.
问题 如果某一随机事件，可能出现的结果是无限个，或每种可能结果发生的可能性不一致，那么我们无法用列举法求其概率，这时我们能够用频率来估计概率吗？
从一定高度落下的图钉，着地时会有哪些可能的结果？
其中顶帽着地的可能性大吗？
　做做试验来解决这个问题.
(1) 选取 20 名同学，每位学生依次使图钉从高处落下 20 次，并根据试验结果填写下表.
(2) 根据上表画出统计图表示“顶帽着地”的频率.
(3) 这个试验说明了什么问题？
在图钉落地试验中，“钉帽着地”的频率随着试验次数的增加，稳定在常数 56.5% 附近.
例1 某篮球队教练记录该队一名前锋练习罚篮的结果如下： (1) 填表(精确到0.001)； (2) 比赛中该前锋队员上篮得分并造成对手犯规，罚篮一 次，你能估计这次他能罚中的概率是多少吗？
解：从表中的数据可以发现，随着练习次数的增加，该前锋罚篮命中的频率稳定在 0.8 左右，所以估计他这次能罚中的概率约为 0.8.
例2 瓷砖生产受烧制时间、温度、材质的影响，一块砖坯放在炉中烧制，可能成为合格品，也可能成为次品或废品，究竟发生哪种结果，在烧制前无法预知，所以这是一种随机现象. 而烧制的结果是“合格品”是一个随机事件，这个事件的概率称为“合格品率”. 由于烧制结果不是等可能的，我们常用“合格品”的频率作为“合格品率”的估计值.
某瓷砖厂对瓷砖进行质量抽检，结果如下：
(1)计算上表中合格品率的各频率 (精确到 0.001)；(2)估计这种瓷砖的合格品率 (精确到 0.01)；(3)若该厂本月生产该型号瓷砖 500000 块，试估计合格 品数.
(1) 逐项计算，填表如下：
(2) 观察上表，可以发现，当抽取的瓷砖数 n ≥ 400 时，合格品率 稳定在 0.962 的附近，所以我们可取 p = 0.96 作为该型号瓷砖的合格品率的估计.(3) 500000×96% = 480000 (块)，可以估计该型号合格品数为 480000 块.
联系： 频率 概率
事件发生的可能性大小
在实际问题中，若事件的概率未知，常用频率作为它的估计值.
区别：频率本身是随机的，在试验前不能确定，做同样次数或不同次数的重复试验得到的频率都可能不同；而概率是一个确定数，是客观存在的，与每次试验无关.
用样本(频率)估计总体(概率)
频率稳定时可看作是概率但概率与频率无关