四川省达州市万源中学2023届九年级下学期第三次月考数学试卷(含解析)

这是一份四川省达州市万源中学2023届九年级下学期第三次月考数学试卷(含解析)，共22页。试卷主要包含了请将答案正确填写在答题卡上等内容，欢迎下载使用。
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
一、单选题（本大题共10小题，每个题3分，共30分；在每小题给出的四个选项中，只有一个是符号题目要求的）
1. 如图所示，已知四边形ABCD，R、P分别是DC、BC上的点，点E、F分别是AP、RP的中点，当点P在边BC上从点B向点C移动，且点R从点D向点C移动时，那么下列结论成立的是（ ）
A. 线段EF的长逐渐增大
B. 线段EF的长逐渐减少
C. 线段EF的长不变
D. △ABP和△CRP的面积和不变
答案：A
解析：
详解：解：∵E，F分别是AP，RP中点，
∴EF=AR，
当点P在边BC上点B，且点R在点D时，EF=AR=AD，
当点P在边BC上从点B向点C移动，且点R从点D向点C移动时，AR的长度逐渐增大，
∴线段EF的长度逐渐增大，
S△ABP+S△CRP=BC(AB+CR)，
∵CR随着点R的运动而减小，
∴△ABP和△CRP的面积和逐渐减小，
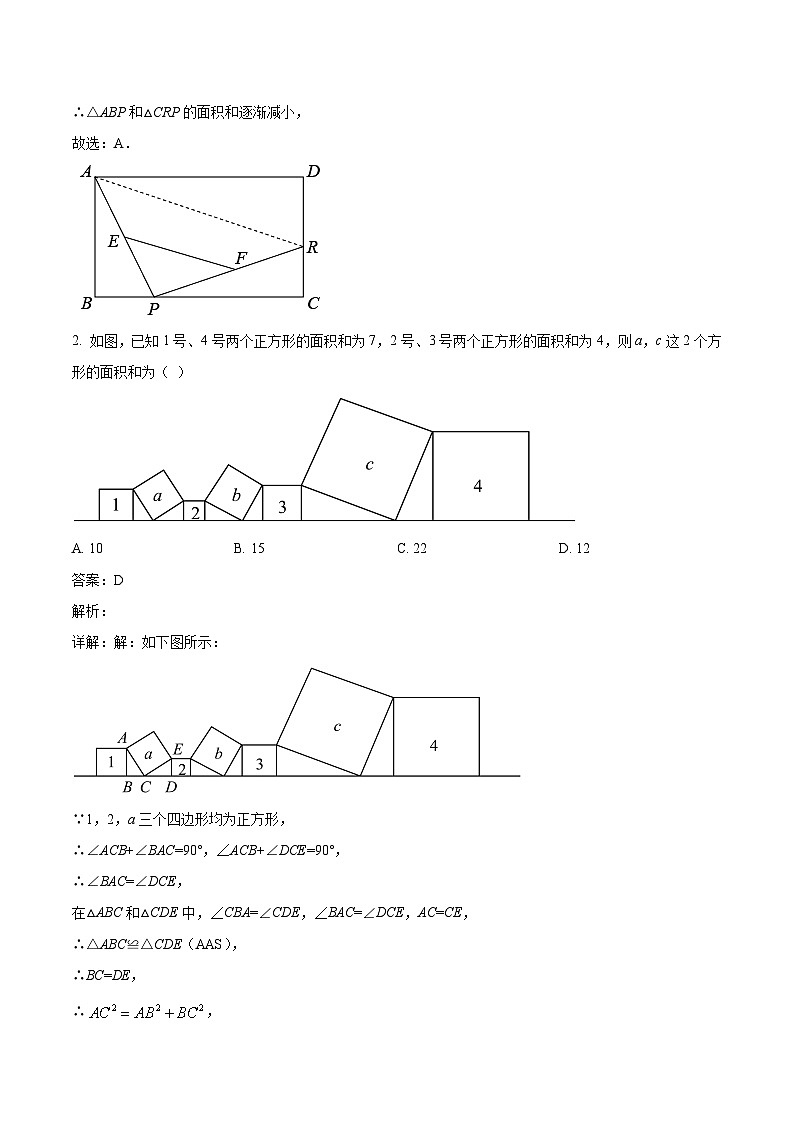
故选：A．
2. 如图，已知1号、4号两个正方形的面积和为7，2号、3号两个正方形的面积和为4，则a，c这2个方形的面积和为（ ）

A. 10B. 15C. 22D. 12
答案：D
解析：
详解：解：如下图所示：

∵1，2，a三个四边形均为正方形，
∴∠ACB+∠BAC=90°，∠ACB+∠DCE=90°，
∴∠BAC=∠DCE，
在△ABC和△CDE中，∠CBA=∠CDE，∠BAC=∠DCE，AC=CE，
∴△ABC≌△CDE（AAS），
∴BC=DE，
∴，
∴正方形a的面积等于正方形1的面积加上正方形2的面积，
即Sa=S1+S2，
同理可得出：Sc=S3+S4，
∴Sa+Sc=S1+S2+S3+S4=7+5=12．
故选：D．
3. 在平面直角坐标系中，已知点A(﹣2，3)，若将OA绕原点O逆时针旋转180°得到OA'，则点A'在平面直角坐标系中的位置是在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
答案：D
解析：
详解：
如图，∵点A(−2，3)，若将OA绕原点O逆时针旋转180°得到OA'，
∴A'的坐标是(2，−3)，
即点A'在第四象限．
故选：D．
4. 已知两点、，以原点为位似中心，将缩小为原来的，则点的对应点的坐标为（ ）．
A. B. C. D.
答案：A
解析：
详解：以原点为位似中心，将缩小为原来的，
∵点的坐标为
∴点的对应点的坐标为，即
故选：A．
5. 如图，ABCD是正方形， G是BC上（除端点外）的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F，给出以下结论：①△AED≌△BFA；②DE﹣BF=EF；③△BGF∽△DAE；④DE﹣BG=FG，其中正确的有（ ）

A. 1个B. 2个C. 3个D. 4个
答案：C
解析：
详解：解：∵四边形ABCD是正方形，
∴AB=AD，AD∥BC，
∵DE⊥AG，BF∥DE，
∴BF⊥AG，
∴∠AED=∠DEF=∠BFE=90°，
∵∠BAF+∠DAE=90°，∠DAE+∠ADE=90°，
∴∠BAF=∠ADE，
∴△AED≌△BFA（AAS）；故A正确；
∴DE=AF，AE=BF，
∴DE-BF=AF-AE=EF，故B正确；
∵AD∥BC，
∴∠DAE=∠BGF，
∵DE⊥AG，BF⊥AG，
∴∠AED=∠GFB=90°，
∴△BGF∽△DAE，故C正确；
∵DE，BG，FG没有等量关系，
故不能判定DE-BG=FG正确．故D错误（也可以用排除法判断）；
故选C．
6. 如图，在中，，，．按以下步骤作图：①以点为圆心，适当长度为半径作弧，分别交边，于点，；②分别以点，为圆心，大于的长为半径作弧，两弧在内交于点；③作射线，交的延长线于点，则的长为（ ）
A. B. 2C. D.
答案：B
解析：
详解：由题意知：DM平分∠ADC，
∴ ∠ADM＝∠MDC，
∵ 四边形ABCD是平行四边形，
∴ AD∥CM，AB＝CD，
∴ ∠ADM＝∠DMC，
∴∠DMC＝∠MDC，
∴CD＝CM，
∵AB＝4，BC＝2，
∴CM＝CD＝4，
∴BM＝CM－BC＝2，
故选：B．
7. 如图，要判定是菱形，需要添加的条件是（ ）
A. B. C. D.
答案：D
解析：
详解：解：根据邻边相等的平行四边形是菱形，可知选项D正确，
故选：D．
8. 如图，要设计一幅宽10cm，长15cm的图案，其中有两横两竖的彩条，横、竖彩条的宽度比为．如果要使彩条所占面积是图案面积的四分之一，设横彩条的宽度是3xcm，则可列方程为（ ）
A. B.
C. D.
答案：B
解析：
详解：解：设横彩条的宽度是3xcm，则竖彩条的宽度是2xcm，由题意得
，
故选：B
9. 如图，在△ABC中，∠ACB＝90°，∠B＝40°，分别以点A和点B为圆心，以相同的长（大于AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E，连接CD，则∠CDE等于（ ）
A. 8°B. 10°C. 15°D. 20°
答案：B
解析：
详解：解：由题意得MN垂直平分AB，
∴AD=BD，∠ADE=90°，
∵∠ACB＝90°，
∴CD=AD=BD，
∴∠BCD=∠B＝40°，
∴∠ADC=2∠B＝80°，
∴∠CDE=∠ADE-∠ADC=10°，
故选：B．
10. 如图，D是△ABC内一点，BD⊥CD，BD＝4，CD＝3，四边形EFGH的周长为11，E、F、G、H分别是AB、AC、CD、BD的中点，AD的长为（ ）
A. 6B. 5C. 4D. 7
答案：A
解析：
详解：解：∵BD⊥CD，BD＝4，CD＝3，
∴BC＝5，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴EF∥HG，EF＝HG＝BC＝，
∵四边形EFGH的周长为11，
∴EH＝FG=，
∴AD＝2GF＝6，
故选A．
二、填空题（本大题共6小题，每个题3分，共18分，把答案写在题中横线上．）
11. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，AD＝3，BD＝6，CD的长为_____．

答案：3
解析：
详解：∵∠ACB=90°，CD⊥AB于点D，
∴∠ADC=∠CDB=90°，∠A+∠B=90°，∠B+∠BCD=90°，
∴∠A=∠BCD，
∴△ADC∽△CDB，
∴AD：CD=CD：BD，
∴CD2＝AD•BD＝3×6=18，
解得，CD＝3，
故答案为3．
12. 如图，菱形ABCD的顶点C在直线MN上，若∠1＝50°，∠2＝20°，则∠BDC的度数为 ______．
答案：35°##35度
解析：
详解：解：∵∠1＝50°，∠2＝20°，
∴∠BCD=180°-∠1-∠2=110°，
∵四边形ABCD是菱形，
∴∠BCD+∠ADC=180°，
∴∠ADC=70°，
∴∠BDC=∠ADC=35°，
故答案为：35°．
13. 如图，在Rt△ABC中，∠ACB=90°，点H、E、F分别是边AB、BC、CA的中点，EF+CH=8，则CH的值为__________．
答案：4
解析：
详解：∵在Rt△ABC中，∠ACB＝90°，点H，E，F分别是边AB，BC，CA的中点，
∴EF＝AB，CH＝AB，
∴EF＝CH，
∵EF＋CH＝8，
∴CH＝EF＝×8＝4，
故答案为：4．
14. 关于x的一元二次方程的两个根分别是与，则________．
答案：2
解析：
详解：解：根据题意得，
解得，
故答案为：2．
15. 一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球（除颜色外其余都相同），其中红球有2个，黑球有1个，绿球有3个，第一次任意摸出一个球（不放回），第二次再摸出一个球，则两次摸到的都是红球的概率为_____．
答案：
解析：
详解：解：列表如下：
所有等可能的情况有30种，其中两次都是红球的情况有2种，
则P==．
故答案为．
16 如图，矩形ABCD中，AD＝1，AB＝.将矩形ABCD绕着点B顺时针旋转90°得到矩形．联结，分别交边CD，于E、F．如果AE＝，那么＝______．

答案：
解析：
详解：解：∵将矩形ABCD绕着点B顺时针旋转90°得到矩形A′BC′D′，
∴AD=A'D'=1，AB=A'B=k，∠A'=∠DAB=90°=∠DCB=∠ABC，
∴A'D'∥BA∥CD
∴∠A'D'F=∠FEC=∠DEA，且∠D=∠A'=90°，
∴△ADE∽△FA'D'，
∴，且AE＝，
∴，，
∵∠A'=∠DCF=90°，∠A'FD'=∠EFC，
∴△A'D'F∽△CEF，
∴，
∴，
∴
故答案为：

三、解答题（本大题共9小题，第17、18、19每个题6分，第20、21每个题8分，第22、23每个题9分，第24、25每个题10分，共72分，解答时应写出必要文字证明、证明过程或演算步骤．）
17. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，的顶点都在格点上，建立如图所示的平面直角坐标系．
（1）将向左平移5个单位长度后再向下平移3个单位长度，请画出经过两次平移后得到的；
（2）以原点O为位似中心，将缩小，使变换后得到的与对应边的比为1：2．请在第三象限内画出，并写出点的坐标．
答案：（1）画图见解析
（2）画图见解析，
解析：
小问1详解：
解：如图所示，即为所求；
小问2详解：
解：如图所示，即为所求；
∴．
18. 已知和中，有,且和的周长之差为15厘米，求和的周长.
答案：分别是30厘米和45厘米.
解析：
详解：解：设和的周长分别是x厘米和y厘米.

①..
由题意可得： ②
由①式得 ③
将③式代入①式得：
...
将代入②式得：
...
答：和的周长分别是30厘米和45厘米.
19. 如图，在平行四边形中，点E是边的中点，连接并延长交的延长线于点F，连接．

（1）求证：；
（2）求证：四边形是平行四边形．
答案：（1）见解析 （2）见解析
解析：
小问1详解：
证明：∵在平行四边形中，，
∴，
∵点E是边的中点，
∴，
在和中
,
∴．
小问2详解：
证明：∵，
∴，
∵，
∴四边形是平行四边形．
20. 如图①，在四边形中，，点从点出发，沿射线以每秒2个单位长度的速度向右运动，同时点从点出发，沿方向以每秒1个单位长度的速度向点运动．当点到达点时，点停止运动，设点运动时间为秒．
（1）求的长；
（2）当运动停止时，求线段的长；
（3）在运动的过程中，是否存在某一时刻，使以为顶点的四边形为平行四边形？若存在，请求出的值，若不存在，请说明理由．
（4）如图②，若点为边上一点，且，当是以为腰的等腰三角形时，求的值．
答案：（1）4 （2）12
（3）存在，t的值为2或6
（4）1或或4
解析：
小问1详解：
解：如图①，过点作，于点，
∵，
∴四边形是矩形，
∴，
∴，
在中，由勾股定理得，
∴，
∴的长为；
小问2详解：
解：由题意知，运动停止时，点运动时间为秒，
∴，
∴，
∴运动停止时， 的长为12；
小问3详解：
解：由题意知，以 为顶点的四边形为平行四边形，分两种情况求解：
①当为平行四边形的边，则在点左侧，，，
∵，
∴，
解得；
∴当秒时， 以 为顶点的四边形为平行四边形；
②当为平行四边形的对角线，在点右侧，，，
∵，
∴，
解得，
∴当时，以 为顶点的四边形为平行四边形；
综上所述，存在，当或时，以 为顶点的四边形为平行四边形；
小问4详解：
解：由题意知，当是以为腰的等腰三角形时，分两种情况求解：
①当时，如图②，
在中，由勾股定理得，，
∴；
②当时，如图②，过作于，
由题意知，四边形是矩形，
∴，
在中，由勾股定理得，，
∴或，
∴或，
综上所述，当或或时，是以为腰的等腰三角形．
21. 如图，在平行四边形ABCD中，对角线AC和BD交于点O，．
（1）请用尺规完成基本作图：作出的角平分线交AC于点M，交CD交于点N；（尺规作图保留作图痕迹，不写作法）
（2）在（1）的条件下，连接ON，若，，求的周长．
答案：（1）见解析 （2）10
解析：
小问1详解：
解：如图即为所求．
小问2详解：
解：∵平行四边形ABCD
∴OD=OB=BD=4,DC=AD
∵
∴DC=AD=4
∴OB=DC=4
∵BN是的角平分线
∴BN是线段OC的垂直平分线
∴ON=CN
∴的周长=OD+ON+DN=OD+NC+DN=OD+CD=4+6=10．
22. 如图，在由边长为1个单位长度的小正方形组成的网格中，给出以格点（网格线的交点）为端点的线段及格点O．
（1）将线段绕点O顺时针旋转得到线段（点A，B的对应点分别为C，D），请画出线段．
（2）以线段为一边，在网格内作出一个周长最大的等腰，点E在格点上．
答案：（1）见解析 （2）见解析
解析：
小问1详解：
如图，线段即为所求；
小问2详解：
如图，等腰即为所求．
23. 我省某地区为了了解2018年初中毕业生的毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向：A．读普通高中；B．读职业高中；C．直接进入社会就业；D．其他(如出国等)进行数据统计，并绘制了两幅不完整的统计图(如图①，图②)．
（1）填空：该地区共调查了________名九年级学生；
（2）将两幅统计图中不完整的部分补充完整；
（3）若该地区2018年初中毕业生共有3500人，请估计该地区2018年初中毕业生中读普通高中的人数；
（4）老师想从甲、乙、丙、丁4位同学中随机选择两位同学了解他们毕业后的去向情况，请用画树状图或列表的方法求选中甲同学的概率．

答案：（1）200 （2）图见解析
（3）1925 （4）
解析：
小问1详解：
解：（1）该地区调查的九年级学生数为：（人），
故答案为：200；
小问2详解：
解：B去向的学生有：（人），
C去向所占的百分比为：，
补全的统计图如右图所示，
小问3详解：
解：该地区今年初中毕业生中读普通高中的学生有：（人），
即该地区今年初中毕业生中读普通高中的学生有1925人；
小问4详解：
解：由题意可得，

，
即选中甲同学的概率是．
24. 已知关于x的一元二次方程有两个相等的实数根，求k的值与方程的根．
答案：
解析：
详解：解：依题意可得，解得，
把代入得，
即，
解得．
25. 如图，在平面直角坐标系中，直线y＝kx+b经过点A（4，0）、B（0，2），点P是x轴正半轴上的动点，过点P作PC⊥x轴，交直线AB于点C，以OA、AC为边构造平行四边形OACD．设点P的横坐标为m．
（1）若四边形OACD恰是菱形，请求出m的值；
（2）在（1）的条件下，y轴上是否存在点Q，连结CQ，使得∠OQC+∠ODC＝180°？若存在，请求出所有符合条件的点Q的坐标；若不存在，请说明理由．

答案：（1）m＝；（2）Q（0，4﹣8）．
解析：
详解：解：（1）∵A（4，0）、B（0，2），
∴OA＝4，OB＝2，
∴AP＝4﹣m，
∵PC∥OB，
∴△OAB∽△PAC，
∴,即，
∴PC＝2﹣，
∴AC＝，
∵四边形OACD恰是菱形，
∴OA＝AC，即（4﹣m）＝4，
解得，m＝；
（2）∵四边形OACD恰是菱形，
∴∠ODC＝∠CAO，

∵∠CDO+∠OQC＝180°，∠OQC+∠BQC＝180°，
∴∠BQC＝∠BAO，
∵∠QBC＝∠ABO，
∴△BQC∽△BAO，
∴，
∵AC＝,AB＝，
∴BC＝AB﹣AC＝2﹣4，
∴BQ＝＝10﹣4，
∴OQ＝OB﹣BQ＝4﹣8
∴Q（0，4﹣8）．