

所属成套资源:中考数学一轮复习满分突破(全国通用)(原卷版+解析)
中考数学一轮复习满分突破(全国通用)专题07一线三垂直与一线三等角(原卷版+解析)
展开
这是一份中考数学一轮复习满分突破(全国通用)专题07一线三垂直与一线三等角(原卷版+解析),共46页。试卷主要包含了基础知识回顾,模型的概述等内容,欢迎下载使用。
1)三角形内角和定理:三角形三个内角和等于180°
2)1平角=180度
二、模型的概述:
1)一线三垂直模型
[模型概述]只要出现等腰直角三角形,可以过直角点作一条直线,然后过45°顶点作直线的垂线,构造三垂直,所得两个直角三角形全等。根据全等三角形倒边,得到线段之间的数量关系。
基础 构造1 构造2
一线三垂直模型一:如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE,则∆ABD≌∆BCE,DE=AD+EC
证明:∵CE⊥DE,AD⊥DE,AB⊥BC ∴∠CEB=∠ADB=∠ABC =90°
∴∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3
在∆ABD和∆BCE中,
∠1=∠3
∠CEB=∠ADB =90° ∴∆ABD≌∆BCE(AAS) ∴AD=BE,EC=BD
AB=BC 则DE=BE+BD= AD+ EC
一线三垂直模型二:如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE,则∆ABD≌∆BCE,DE=AD-EC
证明:∵CE⊥DE,AD⊥DE,AB⊥BC ∴∠CEB=∠ADB=∠ABC =90°
∴∠A+∠ABD=90°,∠ABD+∠CBE=90° ∴∠A=∠CBE
在∆ABD和∆BCE中,
∠A=∠CBE
∠CEB=∠ADB =90° ∴∆ABD≌∆BCE(AAS) ∴AD=BE,EC=BD
AB=BC
则DE=BE-BD= AD- EC
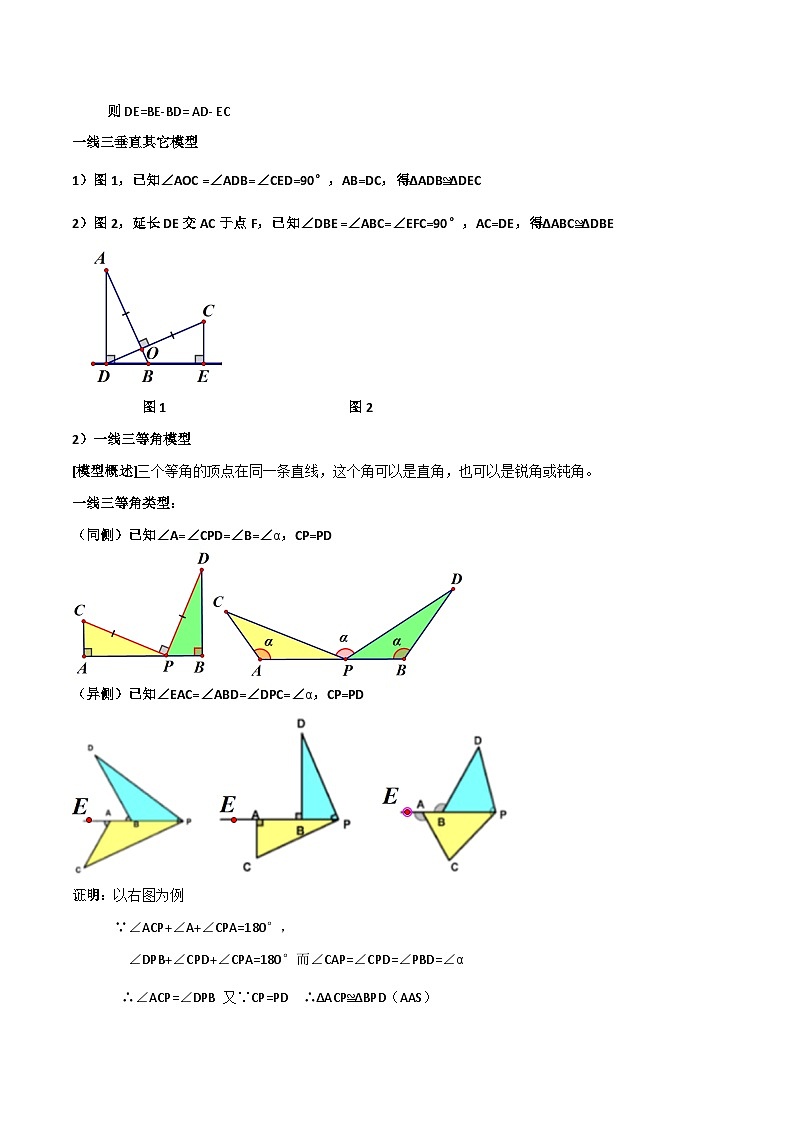
一线三垂直其它模型
1)图1,已知∠AOC =∠ADB=∠CED=90°,AB=DC,得∆ADB≌∆DEC
2)图2,延长DE交AC于点F,已知∠DBE =∠ABC=∠EFC=90°,AC=DE,得∆ABC≌∆DBE
图1 图2
2)一线三等角模型
[模型概述]三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角。
一线三等角类型:
(同侧)已知∠A=∠CPD=∠B=∠α,CP=PD
(异侧)已知∠EAC=∠ABD=∠DPC=∠α,CP=PD
证明:以右图为例
∵∠ACP+∠A+∠CPA=180°,
∠DPB+∠CPD+∠CPA=180°而∠CAP=∠CPD=∠PBD=∠α
∴∠ACP=∠DPB 又∵CP=PD ∴∆ACP≌∆BPD(AAS)
【基础过关练】
1.如下图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是( )
A.6cmB.1.5cmC.3cmD.4.5cm
2.如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3B.2C.D.
3.如图,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=6cm,DE=2cm,则BD等于( )
A.6cmB.8cmC.10cmD.4cm
4.如图,中,,则点B的坐标为________.
5.如图,为等腰直角三角形,若A(−3,0),C(0,2),则点B的坐标为_________.
6.如图所示,中,.直线l经过点A,过点B作于点E,过点C作于点F.若,则__________.
7.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=50cm,OB=28cm,则点C离地面的距离是____ cm.
8.如图,AB=BC, AB⊥BC, AE⊥BD于F,BC⊥CD, 求证:EC=AB-CD.
【提高测试】
1.如图,在平面直角坐标系中,点A、B分别在x轴的负半轴和正半轴上,以AB为边向上作正方形ABCD,四边形OEFG是其内接正方形,若直线OF的表达式是y=2x,则的值为( )
A.B.C.D.
2.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是______.
3.已知直线l经过正方形ABCD的顶点A,过点B和点D分别作直线的垂线BM和DN,垂足分别为点M、点N,如果,,那么点M和点N之间的距离为_______.
4.如图,已知中,,,分别过、向过的直线作垂线,垂足分别为.
(1)如图1,过的直线与斜边不相交时,直接写出线段、、的数量关系是______;
(2)如图2,过的直线与斜边相交时,探究线段、、的数量关系并加以证明;
(3)在(2)的条件下,如图3,直线交于点,延长交于点,连接、、,若,,,四边形的面积是90,求的面积.
5.如图1所示,已知中,,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,求证:;
(2)若直线m绕点C旋转到图2所示的位置时(),其余条件不变,猜想与,有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时()其余条件不变,问与,的关系如何?直接写出猜想结论,不需证明.
6.如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
7.在平面直角坐标系中,点的坐标为,点为轴正半轴上的一个动点,以为直角顶点,为直角边在第一象限作等腰Rt.
(1)如图1,若,则点的坐标为______;
(2)如图2,若,点为延长线上一点,以为直角顶点,为直角边在第一象限作等腰Rt,连接,求证:;
(3)如图3,以为直角顶点,为直角边在第三象限作等腰Rt.连接,交轴于点,求线段的长度.
8.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
9.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在中,,,直线l经过点A,直线l,直线l,垂足分别为点D,E.求证:.
(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在中,,D,A,E三点都在直线l上,并且有,其中为任意锐角或钝角.请问结论是否成立?若成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过的边AB,AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高.延长HA交EG于点I.若,则______.
10.如图,在ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;
(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.
11.综合与探究:在平面直角坐标系中,已知A(0,a),B(b,0)且a,b满足(a﹣3)2+|a﹣2b﹣1|=0
(1)求A,B两点的坐标
(2)已知△ABC中AB=CB,∠ABC=90°,求C点的坐标
(3)已知AB=,试探究在x轴上是否存在点P,使△ABP是以AB为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
12.如图,在中,.
(1)如图①所示,直线过点,于点,于点,且.求证:.
(2)如图②所示,直线过点,交于点,交于点,且,则是否成立?请说明理由.
13.通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC= ,BC=AE.我们把这个数学模型称为“K字”模型或“一线三等角”模型;
(2)如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
(深入探究)
(3)如图,已知四边形ABCD和DEGF为正方形,△AFD的面积为S1,△DCE的面积为S2,则有S1 S2(填“>、=、<”)
14.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
15.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
专题07 一线三垂直与一线三等角
一、基础知识回顾
1)三角形内角和定理:三角形三个内角和等于180°
2)1平角=180度
二、模型的概述:
1)一线三垂直模型
[模型概述]只要出现等腰直角三角形,可以过直角点作一条直线,然后过45°顶点作直线的垂线,构造三垂直,所得两个直角三角形全等。根据全等三角形倒边,得到线段之间的数量关系。
基础 构造1 构造2
一线三垂直模型一:如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE,则∆ABD≌∆BCE,DE=AD+EC
证明:∵CE⊥DE,AD⊥DE,AB⊥BC ∴∠CEB=∠ADB=∠ABC =90°
∴∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3
在∆ABD和∆BCE中,
∠1=∠3
∠CEB=∠ADB =90° ∴∆ABD≌∆BCE(AAS) ∴AD=BE,EC=BD
AB=BC 则DE=BE+BD= AD+ EC
一线三垂直模型二:如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE,则∆ABD≌∆BCE,DE=AD-EC
证明:∵CE⊥DE,AD⊥DE,AB⊥BC ∴∠CEB=∠ADB=∠ABC =90°
∴∠A+∠ABD=90°,∠ABD+∠CBE=90° ∴∠A=∠CBE
在∆ABD和∆BCE中,
∠A=∠CBE
∠CEB=∠ADB =90° ∴∆ABD≌∆BCE(AAS) ∴AD=BE,EC=BD
AB=BC
则DE=BE-BD= AD- EC
一线三垂直其它模型
1)图1,已知∠AOC =∠ADB=∠CED=90°,AB=DC,得∆ADB≌∆DEC
2)图2,延长DE交AC于点F,已知∠DBE =∠ABC=∠EFC=90°,AC=DE,得∆ABC≌∆DBE
图1 图2
2)一线三等角模型
[模型概述]三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角。
一线三等角类型:
(同侧)已知∠A=∠CPD=∠B=∠α,CP=PD
(异侧)已知∠EAC=∠ABD=∠DPC=∠α,CP=PD
证明:以右图为例
∵∠ACP+∠A+∠CPA=180°,
∠DPB+∠CPD+∠CPA=180°而∠CAP=∠CPD=∠PBD=∠α
∴∠ACP=∠DPB 又∵CP=PD ∴∆ACP≌∆BPD(AAS)
【基础过关练】
1.如下图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是( )
A.6cmB.1.5cmC.3cmD.4.5cm
【答案】C
【分析】本题可通过全等三角形来求BE的长.△BEC和△CDA中,已知了一组直角,∠CBE和∠ACD同为∠BCE的余角,AC=BC,可据此判定两三角形全等;那么可得出的条件为CE=AD,BE=CD,因此只需求出CD的长即可.而CD的长可根据CE即AD的长和DE的长得出,由此可得解.
【详解】解:∵∠ACB=90°,BE⊥CE,
∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°;
∴∠ACD=∠CBE,又AC=BC,
∴△ACD≌△CBE;
∴EC=AD,BE=DC;
∵DE=6cm,AD=9cm,则BE的长是3cm.
故选C.
【点睛】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
2.如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3B.2C.D.
【答案】A
【分析】根据等腰三角形的性质得到∠B=∠C,推出∠BAD=∠CDE,根据线段垂直平分线的性质得到AD=ED,根据全等三角形的性质得到CD=AB=9,BD=CE,即可得到结论.
【详解】解:∵AB=AC=9,
∴∠B=∠C,
∵∠ADE=∠B,∠BAD=180°﹣∠B﹣∠ADB,∠CDE=180°﹣∠ADE﹣∠ADB,
∴∠BAD=∠CDE,
∵AE的中垂线交BC于点D,
∴AD=ED,
在△ABD与△DCE中,
,
∴△ABD≌△DCE(AAS),
∴CD=AB=9,BD=CE,
∵CD=3BD,
∴CE=BD=3
故选:A.
【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质,全等三角形的性质,属于基础题.
3.如图,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=6cm,DE=2cm,则BD等于( )
A.6cmB.8cmC.10cmD.4cm
【答案】B
【分析】根据题意证明即可得出结论.
【详解】解:∵AB⊥BD,ED⊥BD,
∴,
∵∠ACE=90°,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
故选:B.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理以及性质定理是解本题的关键.
4.如图,中,,则点B的坐标为________.
【答案】(4,1)
【分析】如图,过点B作BD⊥x轴于D,根据点A、点C坐标可得OA、OC的长,根据同角的余角相等可得∠OAC=∠DCB,利用AAS可证明△OAC≌△DCB,根据全等三角形的性质可得BD=OC,CD=OA,即可求出OD的长,进而可得答案.
【详解】如图,过点B作BD⊥x轴于D,
∵A(0,3),C(1,0),
∴OA=3,OC=1,
∵∠ACB=90°,
∴∠OCA+∠DCB=90°,
∵∠OAC+∠OCA=90°,
∴∠OAC=∠DCB,
在△OAC和△DCB中,,
∴△OAC≌△DCB,
∴BD=OC=1,CD=OA=3,
∴OD=OC+CD=4,
∴点B坐标为(4,1).
故答案为:(4,1)
【点睛】本题考查坐标与图形及全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.
5.如图,为等腰直角三角形,若A(−3,0),C(0,2),则点B的坐标为_________.
【答案】(2,−1)
【分析】过点B作轴于点T.证明,可得结论.
【详解】解:如图中,过点B作轴于点T.
∵A(−3,0),C(0,2),
∴,,
∵,
∴,,
∴,
在和中,,
∴(AAS),
∴ ,,
∴,
∴B(2,−1),
故答案为:(2,−1).
【点睛】本题考查了坐标与图形,等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
6.如图所示,中,.直线l经过点A,过点B作于点E,过点C作于点F.若,则__________.
【答案】7
【分析】根据全等三角形来实现相等线段之间的关系,从而进行计算,即可得到答案;
【详解】解:∵BE⊥l,CF⊥l,
∴∠AEB=∠CFA=90°.
∴∠EAB+∠EBA=90°.
又∵∠BAC=90°,
∴∠EAB+∠CAF=90°.
∴∠EBA=∠CAF.
在△AEB和△CFA中
∵∠AEB=∠CFA,∠EBA=∠CAF,AB=AC,
∴△AEB≌△CFA.
∴AE=CF,BE=AF.
∴AE+AF=BE+CF.
∴EF=BE+CF.
∵,
∴;
故答案为:7.
【点睛】本题考查了全等三角形的判定和性质,余角的性质,解题的关键是熟练掌握所学的知识,正确的证明三角形全等.
7.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=50cm,OB=28cm,则点C离地面的距离是____ cm.
【答案】28
【分析】作CD⊥OB于点D,依据AAS证明,GMF,再根据全等三角形的性质即可得到结论.
【详解】解:过点C作CD⊥OB于点D,如图,
∴
∵是等腰直角三角形
∴AB=CB,
∴
又
∴
在和中,
∴
∴
故答案为:28.
【点睛】本题主要考查了等腰直角三角形的性质、三角形全等的判定与性质,正确作出辅助线构造全等三角形是解答本题的关键.
8.如图,AB=BC, AB⊥BC, AE⊥BD于F,BC⊥CD, 求证:EC=AB-CD.
【答案】见解析
【分析】利用证明出△ABE≌△BCD,在通过等量代换进行解答.
【详解】证明:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠ACD=90°
∴∠AEB+∠A=90°
∵AE⊥BD
∴∠BFE=90°
∴∠AEB+∠FBE=90°
∴∠A=∠FBE,
又∵AB=BC,
∴△ABE≌△BCD,
∴AB=BC,BE=CD,
∴EC=BC-BE=AB-CD
【点睛】本题考查了三角形全等的判定及性质,解题的关键是掌握三角形的判定定理,再利用等量代换的思想来间接证明.
【提高测试】
1.如图,在平面直角坐标系中,点A、B分别在x轴的负半轴和正半轴上,以AB为边向上作正方形ABCD,四边形OEFG是其内接正方形,若直线OF的表达式是y=2x,则的值为( )
A.B.C.D.
【答案】B
【分析】根据正方形性质易得,从而可得、,设OB=a,BG=b,可得F点坐标为,根据F点在直线OF上,可求出,然后即可根据正方形面积和勾股定理求出面积比.
【详解】解:在正方形ABCD,正方形OEFG中,,,
∴,
∴ ,
在和中,
∴(AAS)
∴、,
设、,
∴,,
∴点F坐标为,
∵直线OF的表达式是y=2x,
∴,
∴,
∴,
=,
∴,
故选B.
【点睛】本题主要考查了一次函数与几何综合,解题关键是根据正方形性质求证(AAS),从而用参数表示点F坐标,再直线OF解析式求出线段之间关系.
2.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是______.
【答案】50
【分析】易证△AEF≌△BAG,△BCG≌△CDH即可求得AF=BG,AG=EF,GC=DH,BG=CH,即可求得梯形DEFH的面积和△AEF,△ABG,△CGB,△CDH的面积,即可解题.
【详解】解:∵∠EAF+∠BAG=90°,∠EAF+∠AEF=90°,
∴∠BAG=∠AEF,
∵在△AEF和△BAG中,,
∴△AEF≌△BAG(AAS),
同理△BCG≌△CDH,
∴AF=BG,AG=EF,GC=DH,BG=CH,
∵梯形DEFH的面积=(EF+DH)•FH=80,
S△AEF=S△ABG=AF•AE=9,
S△BCG=S△CDH=CH•DH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故答案为:50.
【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEF≌△BAG,△BCG≌△CDH是解题的关键.
3.已知直线l经过正方形ABCD的顶点A,过点B和点D分别作直线的垂线BM和DN,垂足分别为点M、点N,如果,,那么点M和点N之间的距离为_______.
【答案】8或2##2或8
【分析】根据正方形的性质得出∠NAD=∠MBA,再利用全等三角形的判定得出△ABM≌△AND,进而求出MN的值,注意分类讨论.
【详解】如图1,在正方形ABCD中,
∵,,
∴,
∵在和中,
∴(AAS),
∴,,
∴,
如图2,在正方形ABCD中,
∵,,
∴,
∵在和中,
∴(AAS),
∴,,
∴,
综上:或2.
故答案为:8或2.
【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,将直线l与正方形ABCD的位置分类讨论是解题关键.
4.如图,已知中,,,分别过、向过的直线作垂线,垂足分别为.
(1)如图1,过的直线与斜边不相交时,直接写出线段、、的数量关系是______;
(2)如图2,过的直线与斜边相交时,探究线段、、的数量关系并加以证明;
(3)在(2)的条件下,如图3,直线交于点,延长交于点,连接、、,若,,,四边形的面积是90,求的面积.
【答案】(1)数量关系为:EF=BE+CF;(2)数量关系为:EF=BE-CF.证明见详解;(3)S△GHC=15.
【分析】(1)数量关系为:EF=BE+CF.利用一线三直角得到∠BEA=∠AFC=90°,∠EBA=∠FAC,再证△EBA≌△FEC(AAS)可得BE=AF,AE=CF即可;
(2)数量关系为:EF=BE-CF.先证∠BEA=∠AFC=90°,∠EBA+∠EAB=90°,∠EAB+∠FAC= =90°,可得∠EBA=∠FAC,再证△EBA≌△FEC(AAS),可得BE=AF,AE=CF即可;
(3)先由(2)结论EF=BE-CF;,求出BE=AF=12,由,可求FH=2,EH=4,利用对角线垂直的四边形面积可求BG=,再求EG=3,AH= 10,分别求出S△ACF=,S△HCF=,S△AGH=,利用面积差即可求出.
【详解】解:(1)数量关系为:EF=BE+CF.
∵BE⊥EF,CF⊥EF,∠BAC=90°,
∴∠BEA=∠AFC=90°,∠EBA+∠EAB=90°,∠EAB+∠FAC=180°-∠BAC=90°,
∴∠EBA=∠FAC,
在△EBA和△FEC中,
∵,
∴△EBA≌△FAC(AAS),
∴BE=AF,AE=CF,
∴EF=AF+AE=BE+CF;
(2)数量关系为:EF=BE-CF.
∵BE⊥AF,CF⊥AF,∠BAC=90°,
∴∠BEA=∠AFC=90°,∠EBA+∠EAB=90°,∠EAB+∠FAC= =90°,
∴∠EBA=∠FAC,
在△EBA和△FEC中,
∵,
∴△EBA≌△FAC(AAS),
∴BE=AF,AE=CF,
∴EF=AF-AE=BE-CF;
(3)∵EF=BE-CF;,
∴BE=AF=EF+CF=6+6=12,
∵,EH+FH=EF=6,
∴2FH+FH= 6,
解得FH=2,
∴EH=2FH=4,
S四边形ABFG==90,
∴BG=,
∴EG=BG-BE=15-12=3,AH=AE+EH=6+4=10,
∵S△ACF=,S△HCF=,S△AGH=,
∴S△GHC=S△ACF-S△HCF-S△AGH=36-6-15=15.
【点睛】本题考查图形变换探究线段和差问题,感知,探究以及应用,三角形全等判定与性质,三角形面积,四边形面积,与三角形高有关的计算,掌握图形变换探究线段和差问题,感知,探究以及应用,三角形全等判定与性质,三角形面积,四边形面积,与三角形高有关的计算是解题关键.
5.如图1所示,已知中,,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,求证:;
(2)若直线m绕点C旋转到图2所示的位置时(),其余条件不变,猜想与,有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时()其余条件不变,问与,的关系如何?直接写出猜想结论,不需证明.
【答案】(1)见解析;(2),理由见解析;(3),理由见解析
【分析】(1)先证得,,根据证,推出,即可;
(2)类比(1)证得对应的两个三角形全等,由此可推出,,再根据即可得到;
(3)类比(1)证得对应的两个三角形全等,由此可推出,,再根据即可得到.
【详解】(1)证明:,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(2)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(3)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴.
【点睛】本题考查了全等三角形的判定与性质,主要涉及到了全等三角形的判定与性质,等量代换等知识点,难度不大,熟练掌握全等三角形的判定与性质是解决本题的关键.
6.如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
【答案】(1)见解析;(2)见解析;(3)见解析,
【分析】(1)先根据点,,,得到,则由三线合一定理得到,,证明,推出即可证明,得到;
(2)先根据点,得到,则,再证明,即可利用SAS证明得到,再由,可以推出,即;
(3)同样先证明,推出,得到,即可得到,再由,,得到,则,推出.
【详解】证明:(1)如图1,∵点,,,
∴,
∵,
∴,
∵∠AOB=∠AOC=90°,
∴,
∴,
∵,,
∴
∴,
∴,
∴,
∴;
(2)如图2,由(1)得,
∴,
∵,点,
∴,
∴,
∵,,
∴,
∴,
又∵BE=AD,AC=BN,
∴
∴,
∵,
∴,
∴;
(3)如图3,由(1)得,,,,
∵,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,轴轴,
∴,
∵,
∴,
∴
∴,
∴点的坐标为.
【点睛】本题主要考查了坐标与图形,全等三角形的性质与判定,等腰直角三角形的性质与判定等等,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.
7.在平面直角坐标系中,点的坐标为,点为轴正半轴上的一个动点,以为直角顶点,为直角边在第一象限作等腰Rt.
(1)如图1,若,则点的坐标为______;
(2)如图2,若,点为延长线上一点,以为直角顶点,为直角边在第一象限作等腰Rt,连接,求证:;
(3)如图3,以为直角顶点,为直角边在第三象限作等腰Rt.连接,交轴于点,求线段的长度.
【答案】(1)点C(3,7);(2)证明见详解过程;(3)2.
【分析】(1)如图1,过点C作CH⊥y轴,由“AAS”可证△ABO≌△BCH,可得CH=OB=3,BH=AO=4,可求解;
(2)过点E作EF⊥x轴于F,由“AAS”可证△ABO≌△BCH,可得BO=DF=4,OD=EF,由等腰直角三角形的性质可得∠BAO=45°,∠EAF=∠AEF=45°,可得结论;
(3)由(1)可知△ABO≌△BCG,可得BO=GC,AO=BG=4,再由“AAS”可证△CPG≌△FPB,可得PB=PG=2.
(1)
如图1,过点C作CH⊥y轴于H,
∴∠CHB=∠ABC=∠AOB=90°,
∴∠BCH+∠HBC=90°=∠HBC+∠ABO,
∴∠ABO=∠BCH,
在△ABO和△BCH中,
,
∴△ABO≌△BCH(AAS),
∴CH=OB=3,BH=AO=4,
∴OH=7,
∴点C(3,7),
故答案为:(3,7);
(2)
过点E作EF⊥x轴于F,
∴∠EFD=∠BDE=∠BOD=90°,
∴∠BDO+∠EDF=90°=∠BDO+∠DBO,
∴∠DBO=∠EDF,
在△BOD和△DFE中,
,
∴△BOD≌△DFE(AAS),
∴BO=DF=4,OD=EF,
∵点A的坐标为(4,0),
∴OA=OB=4,
∴∠BAO=45°,
∵OA=DF=4,
∴OD=AF=EF,
∴∠EAF=∠AEF=45°,
∴∠BAE=90°,
∴BA⊥AE;
(3)
过点C作CG⊥y轴G,
由(1)可知:△ABO≌△BCG,
∴BO=GC,AO=BG=4,
∵BF=BO,∠OBF=90°,
∴BF=GC,∠CGP=∠FBP=90°,
又∵∠CPG=∠FPB,
∴△CPG≌△FPB(AAS),
∴BP=GP,
∴BP=BG=2.
【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,添加恰当辅助线构造直角三角形是本题的关键.
8.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
【答案】(1)见解析(2)成立,证明见解析(3)△DEF为等边三角形,证明见解析
【分析】(1)因为DE=DA+AE,故由全等三角形的判定AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE;
(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD;
(3)由△ADB≌△CEA得BD=AE,∠DBA =∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=60°,FB=FA,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠FAE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形.
【详解】解:(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD.
又AB=AC,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE;
(2)成立.证明如下:
∵∠BDA =∠BAC=,
∴∠DBA+∠BAD=∠BAD +∠CAE=180°-.
∴∠DBA=∠CAE.
∵∠BDA=∠AEC=,AB=AC,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE;
(3)△DEF为等边三角形.理由如下:
由(2)知,△ADB≌△CEA,BD=AE,∠DBA =∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°.
∴∠DBA+∠ABF=∠CAE+∠CAF.
∴∠DBF=∠FAE.
∵BF=AF,
∴△DBF≌△EAF(SAS).
∴DF=EF,∠BFD=∠AFE.
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°.
∴△DEF为等边三角形.
【点睛】此题考查了全等三角形的性质和判定、等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定,等边三角形的性质和判定.
9.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在中,,,直线l经过点A,直线l,直线l,垂足分别为点D,E.求证:.
(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在中,,D,A,E三点都在直线l上,并且有,其中为任意锐角或钝角.请问结论是否成立?若成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过的边AB,AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高.延长HA交EG于点I.若,则______.
【答案】(1)见解析;(2)结论成立,理由见解析;(3)3.5
【分析】(1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;
(2)由条件可知∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论;
(3)由条件可知EM=AH=GN,可得EM=GN,结合条件可证明△EMI≌△GNI,可得出结论I是EG的中点.
【详解】解:(1)证明:如图1中,∵BD⊥直线l,CE⊥直线l,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(2)解:成立.
理由:如图2中,
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠DBA=∠CAE,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)如图3,过E作EM⊥HI于M,GN⊥HI的延长线于N.
∴∠EMI=∠GNI=90°
由(1)和(2)的结论可知EM=AH=GN
∴EM=GN
在△EMI和△GNI中,
,
∴△EMI≌△GNI(AAS),
∴EI=GI,
∴I是EG的中点.
∴S△AEI=S△AEG=3.5.
故答案为:3.5.
【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.
10.如图,在ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;
(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.
【答案】(1)25°,65°;(2)2,理由见详解;(3)可以,110°或80°.
【分析】(1)利用邻补角的性质和三角形内角和定理解题;
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
【详解】解:(1)∵∠B=40°,∠ADB=115°,
∴∠BAD=180°-∠B-∠ADB=180°-115°-40°=25°,
∵AB=AC,
∴∠C=∠B=40°,
∵∠EDC=180°-∠ADB-∠ADE=25°,
∴∠DEC=180°-∠EDC-∠C=115°,
∴∠AED=180°-∠DEC=180°-115°=65°;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS);
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴△ADE的形状是等腰三角形.
【点睛】本题主要考查学生对等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点的理解和掌握,此题涉及到的知识点较多,综合性较强,但难度不大,属于基础题.
11.综合与探究:在平面直角坐标系中,已知A(0,a),B(b,0)且a,b满足(a﹣3)2+|a﹣2b﹣1|=0
(1)求A,B两点的坐标
(2)已知△ABC中AB=CB,∠ABC=90°,求C点的坐标
(3)已知AB=,试探究在x轴上是否存在点P,使△ABP是以AB为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)A(0,3)、B(1,0);(2)C(4,1);(3)存在,,,
【分析】(1)由平方数和绝对值的非负性可得a﹣3=0,a﹣2b﹣1=0,从而求得a=3,b=1,即可得到A,B两点的坐标.
(2)过点C向轴作垂线,垂足为,结合已知条件可构造一线三等角模型,即可证明,则,,易得点C的坐标.
(3)若△ABP是以AB为腰的等腰三角形,则需分两种情况讨论:①则在B的左侧,;在右侧,;②,则易证,故.
【详解】解:(1)∵a、b满足(a﹣3)2+|a﹣2b﹣1|=0.
∴a﹣3=0,a﹣2b﹣1=0,
∴a=3,b=1,
∴A(0,3)、B(1,0);
(2)如图,过点C向轴作垂线,垂足为,则,
∵,,
∴
在和中,
∵
∴
∴,,
∴C(4,1).
(3)若为腰,则分两种情况讨论:
①当时,
若在B的左侧,则,∴;
若在的右侧,则,∴;
②当时,
∵,∴由等腰三角形三线合一可知,
∴.
综上所述,存在,,.
【点睛】本题考查点的坐标,等腰三角形的性质,掌握一线三等角证全等及等腰三角形的存在性的方法为解题关键.
12.如图,在中,.
(1)如图①所示,直线过点,于点,于点,且.求证:.
(2)如图②所示,直线过点,交于点,交于点,且,则是否成立?请说明理由.
【答案】(1)见解析;(2)仍然成立,理由见解析
【分析】(1)首先根据同角的余角相等得到,然后证明,然后根据全等三角形对应边相等得到,,然后通过线段之间的转化即可证明;
(2)首先根据三角形内角和定理得到,然后证明,根据全等三角形对应边相等得到,最后通过线段之间的转化即可证明.
【详解】证明:(1)∵,,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,,
∵,
∴;
(2)仍然成立,理由如下:
∵,
∵,
∴,
在和中,
,
∴,
∴,,
∵,
∴.
【点睛】此题考查了全等三角形的性质和判定,同角的与相等,三角形内角和定理等知识,解题的关键是根据同角的余角相等或三角形内角和定理得到.
13.通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC= ,BC=AE.我们把这个数学模型称为“K字”模型或“一线三等角”模型;
(2)如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
(深入探究)
(3)如图,已知四边形ABCD和DEGF为正方形,△AFD的面积为S1,△DCE的面积为S2,则有S1 S2(填“>、=、<”)
【答案】(1)DE;(2)见解析;(3)=
【分析】(1)根据全等三角形的性质可直接进行求解;
(2)分别过点D和点E作DH⊥FG于点H,EQ⊥FG于点Q,进而可得∠BAF=∠ADH,然后可证△ABF≌△DAH,则有AF=DH,进而可得DH=EQ,通过证明△DHG≌△EQG可求解问题;
(3)过点D作DO⊥AF交AF于O,过点E作EN⊥OD交OD延长线于N,过点C作CM⊥OD交OD延长线于M,由题意易得∠ADC=∠90°,AD=DC,DF=DE,然后可得∠ADO=∠DCM,则有△AOD≌△DMC,△FOD≌△DNE,进而可得OD=NE,通过证明△ENP≌△CMP及等积法可进行求解问题.
【详解】解:(1)∵,∴;
(2)分别过点D和点E作DH⊥FG于点H,EQ⊥FG于点Q,如图所示:
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴△ABF≌△DAH,
∴AF=DH,
同理可知AF=EQ,
∴DH=EQ,
∵DH⊥FG,EQ⊥FG,
∴,
∵
∴△DHG≌△EQG,
∴DG=EG,即点G是DE的中点;
(3),理由如下:如图所示,过点D作DO⊥AF交AF于O,过点E作EN⊥OD交OD延长线于N,过点C作CM⊥OD交OD延长线于M
∵四边形ABCD与四边形DEGF都是正方形
∴∠ADC=∠90°,AD=DC,DF=DE
∵DO⊥AF,CM⊥OD,
∴∠AOD=∠CMD=90°,∠OAD+∠ODA=90°,∠CDM+∠DCM=90°,
又∵∠ODA+∠CDM=90°,
∴∠ADO=∠DCM,
∴△AOD≌△DMC,
∴,OD=MC,
同理可以证明△FOD≌△DNE,
∴,OD=NE,
∴MC =NE,
∵EN⊥OD,CM⊥OD,∠EPN=∠CMP,
∴△ENP≌△CMP,
∴,
∵,
∴,
∴即.
【点睛】本题主要考查全等三角形的性质与判定、直角三角形的两个锐角互余及等积法,熟练掌握全等三角形的判定条件是解题的关键.
14.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
【答案】(1)①EF= BE-AF;②∠α+ ∠BCA = 180°,理由见解析;(2)不成立,EF=BE+AF,证明见解析
【分析】(1)①求出∠BEC=∠AFC = 90°, ∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE = AF即可得出结论;②求出∠BEC =∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE = AF即可得出结论;
(2)求出∠BEC =∠AFC,∠CBE= ∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE=AF即可得出结论.
【详解】(1)①EF、BE、AF的数量关系:EF= BE-AF,
证明:当α =90°时,∠BEC = ∠CFA =90°,
∵∠BCA = 90°,
∴∠BCE+∠ACF= 90°,
∵∠BCE+∠CBE =90°,
∴∠ACF = ∠CBE,
∵AC = BC,
∴△BCE≌△CAF,
∴BE =CF,CE = AF,
∵CF =CE+EF,
∴EF= CF -CE=BE-AF;
②∠α与∠BCA关系:∠α+ ∠BCA = 180°
当∠α+ ∠BCA = 180°时,①中结论仍然成立;
理由是:如题图2,
∵∠BEC = ∠CFA = ∠α, ,∠α+∠ACB =180°,
又∵
∴∠CBE= ∠ACF,
在△BCE和△CAF中
∴△BCE≌△CAF (AAS),
∴BE =CF,CE = AF,
∴EF= CF-CE= BE -AF;
故答案为: ∠α+ ∠BCA = 180° ;
(2)EF、BE、AF的数量关系:EF=BE+AF,理由如下
∵∠BEC =∠CFA =∠α, ∠α= ∠BCA,
又∵∠EBC +∠BCE+∠BEC = 180° , ∠BCE+∠ACF+∠ACB =180° ,
∴∠EBC +∠BCE =∠BCE+∠ACF
∴∠EBC = ∠ACF,
在△BEC和△CFA中
∴△ABE≌△CFA(AAS)
∴AF = CE,BE = CF
∵EF= CE+CF,
∴EF= BE+AF.
【点睛】本题考查了全等三角形的性质和判定,证明△BCE≌△CAF是解题的关键.
15.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
【答案】[模型呈现]见解析;[模型应用]50;[深入探究]63
【分析】[模型呈现]证明,根据全等三角形的对应边相等得到;
[模型应用]根据全等三角形的性质得到,,,根据梯形的面积公式计算,得到答案;
[深入探究]过点D作于P,过点E作交的延长线于Q,根据全等三角形的性质得到,证明,得到,进而求出,根据三角形的面积公式计算即可.
【详解】[模型呈现]证明:∵,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴;
[模型应用]解:由[模型呈现]可知,,
∴,
则,
故答案为:50;
[深入探究]过点D作于P,过点E作交AG的延长线于Q,
由[模型呈现]可知,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:63.
【点睛】本题考查的是全等三角形的判定和性质、三角形的面积计算,熟记三角形确定的判定定理是解题的关键.
相关试卷
这是一份中考数学二轮复习满分突破几何模型练习专题07 一线三垂直与一线三等角(2份打包,原卷版+解析版),文件包含中考数学二轮复习满分突破几何模型练习专题07一线三垂直与一线三等角原卷版doc、中考数学二轮复习满分突破几何模型练习专题07一线三垂直与一线三等角解析版doc等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
这是一份专题16 一线三等角相似模型 2024年中考数学核心几何模型重点突破(全国通用),文件包含专题16一线三等角相似模型答案详解docx、专题16一线三等角相似模型docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份专题29 一线三等角模型-中考数学总复习真题探究与变式训练(全国通用),文件包含专题29一线三等角模型解析版docx、专题29一线三等角模型原卷版docx等2份试卷配套教学资源,其中试卷共85页, 欢迎下载使用。








