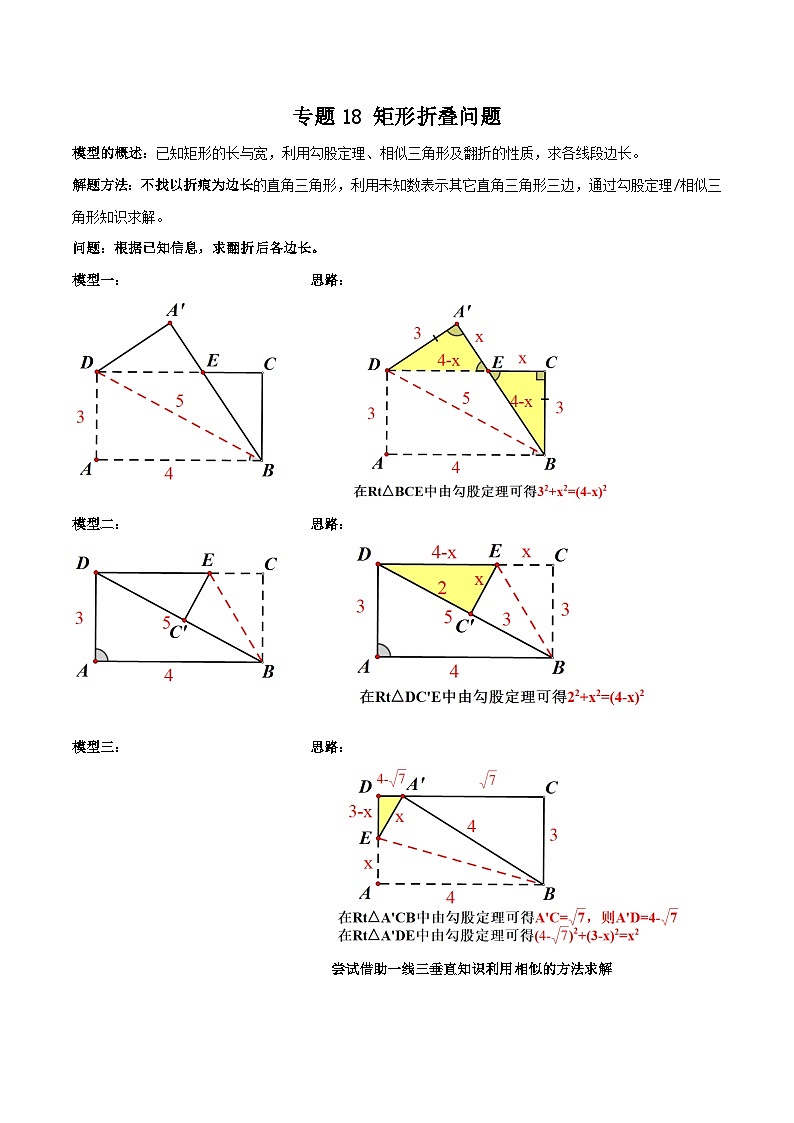
中考数学一轮复习满分突破(全国通用)专题18矩形折叠问题(原卷版+解析)

这是一份中考数学一轮复习满分突破(全国通用)专题18矩形折叠问题(原卷版+解析)，共46页。

解题方法：不找以折痕为边长的直角三角形，利用未知数表示其它直角三角形三边，通过勾股定理/相似三角形知识求解。
问题：根据已知信息，求翻折后各边长。
模型一： 思路：

模型二： 思路：

模型三： 思路：

尝试借助一线三垂直知识利用相似的方法求解
模型四： 思路：
模型五： 思路：
模型六：点M,点N分别为DC，AB中点 思路：

模型七：点A’为BC中点 思路： 过点F作FH⊥AE，垂足为点H
设AE=A’E=x，则BE=8-x
由勾股定理解得x=174 ∴BE=154
由于△EBA’∽△A’CG∽△FD’G
∴A’G=3415 CG=1615 GD’=2615
DF=D’F=AH=134 HE=1 EF=17
【培优过关练】
1．（2022秋·山东青岛·九年级统考期末）如图，在正方形中，，点、分别在边、上，若将四边形沿折叠，点恰好落在边上，则的长度为（ ）
A．B．C．D．
2．（2022秋·江苏徐州·九年级校考阶段练习）如图，在矩形纸片中，点E在边上，沿着折叠使点A落在边上的点F处，若，，则的长为（ ）
A．1B．2C．D．
3．（2022秋·福建泉州·九年级福建省惠安第一中学校联考期中）如图，在平面直角坐标系中，矩形的边在x轴上，边在y轴上，点B的坐标为，将矩形沿对角线折叠，使点B落在D点的位置，且交y轴交于点E，则点D的坐标是（ ）
A．（）B．（，2）C．（）D．
4．（2023春·广东广州·九年级专题练习）如图，矩形纸片中，，，折叠纸片使落在对角线上，折痕为，点的对应点为，那么的长为（ ）
A．1B．C．D．2
5．（2022秋·湖南邵阳·九年级校联考期中）如图，在矩形纸片中，，点E在上，将沿折叠，点恰落在边上的点F处；点在上，将△ABG沿折叠，点恰落在线段上的点处，有下列结论：①；②；③四边形的面积等于；④．其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
6．（2022秋·广东梅州·九年级校考阶段练习）如图，在矩形中，，，点E为的中点，将沿折叠，使点B落在矩形内点F处，连接，则的长为（ ）
A．B．C．D．
7．（2022秋·广西贵港·九年级统考期中）如图，在矩形纸片中，，，M是上的点，且，将矩形纸片沿过点M的直线折叠，使点D落在上的点P处，点C落在点处，折痕为，当与线段交于点H时，则线段的长是（ ）
A．3B．C．4D．
8．（2022秋·山东枣庄·九年级校考期中）如图，边长为2的正方形的对角线与交于点O，将正方形沿直线折叠，点C落在对角线上的点E处，折痕交于点M，则（ ）
A．B．C．D．
9．（2022·辽宁营口·统考中考真题）如图，在矩形中，点M在边上，把沿直线折叠，使点B落在边上的点E处，连接，过点B作，垂足为F，若，则线段的长为（ ）
A．B．C．D．
10．（2022·贵州毕节·统考中考真题）矩形纸片中，E为的中点，连接，将沿折叠得到，连接．若，，则的长是（ ）
A．3B．C．D．
11．（2022·四川宜宾·统考中考真题）如图，在矩形纸片ABCD中，，，将沿BD折叠到位置，DE交AB于点F，则的值为（ ）
A．B．C．D．
12．（2022·浙江湖州·统考中考真题）如图，已知BD是矩形ABCD的对角线，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BE，DF．将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在对角线BD上的点G，H处，连结GF．则下列结论不正确的是（ ）
A．BD＝10B．HG＝2C．D．GF⊥BC
13．（2022·江苏连云港·统考中考真题）如图，将矩形ABCD沿着GE、EC、GF翻折，使得点A、B、D恰好都落在点O处，且点G、O、C在同一条直线上，同时点E、O、F在另一条直线上．小炜同学得出以下结论：①GF∥EC；②AB=AD；③GE=DF；④OC=2OF；⑤△COF∽△CEG．其中正确的是（ ）
A．①②③B．①③④C．①④⑤D．②③④
14．（2021·广西来宾·统考中考真题）如图，矩形纸片，，点，分别在，上，把纸片如图沿折叠，点，的对应点分别为，，连接并延长交线段于点，则的值为（ ）
A．B．C．D．
15．（2011·吉林长春·中考真题）如图，矩形纸片ABCD中，已知AD =8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )
A．3B．4
C．5D．6
16．（2020·广东深圳·统考中考真题）如图，矩形纸片ABCD中，AB=6，BC=12．将纸片折叠，使点B落在边AD的延长线上的点G处，折痕为EF，点E、F分别在边AD和边BC上．连接BG，交CD于点K,FG交CD于点H．给出以下结论：①EF⊥BG；②GE=GF；③△GDK和△GKH的面积相等；④当点F与点C重合时，∠DEF=75°．其中正确的结论共有（ ）
A．1个B．2个C．3个D．4个
17．（2020·内蒙古呼和浩特·中考真题）如图，把某矩形纸片沿，折叠（点E、H在边上，点F，G在边上），使点B和点C落在边上同一点P处，A点的对称点为、D点的对称点为，若，的面积 为8，的面积为2，则矩形的长为（ ）
A．B．C．D．
18．如图，矩形纸片ABCD，AB=4，BC=3，点P在BC边上，将△CDP沿DP折叠，点C落在点E处，PE、DE分别交AB于点O、F，且OP=OF，则cs∠ADF的值为（ ）
A．B．C．D．
19．（2022·山东泰安·统考中考真题）如图，四边形为正方形，点E是的中点，将正方形沿折叠，得到点B的对应点为点F，延长交线段于点P，若，则的长度为___________．
20．（2022·贵州黔东南·统考中考真题）如图，折叠边长为4cm的正方形纸片，折痕是，点落在点处，分别延长、交于点、，若点是边的中点，则______cm．
21．（2022·浙江丽水·统考中考真题）如图，将矩形纸片折叠，使点B与点D重合，点A落在点P处，折痕为．
(1)求证：；
(2)若，求的长．
22．（2022·河南·统考中考真题）综合与实践
综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．

(1)操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM．
根据以上操作，当点M在EF上时，写出图1中一个30°的角：______．
(2)迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．
①如图2，当点M在EF上时，∠MBQ＝______°，∠CBQ＝______°；
②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由．
(3)拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm时，直接写出AP的长．
23．（2022·吉林长春·统考中考真题）【探索发现】在一次折纸活动中，小亮同学选用了常见的A4纸，如图①，矩形为它的示意图．他查找了A4纸的相关资料，根据资料显示得出图①中．他先将A4纸沿过点A的直线折叠，使点B落在上，点B的对应点为点E，折痕为；再沿过点F的直线折叠，使点C落在上，点C的对应点为点H，折痕为；然后连结，沿所在的直线再次折叠，发现点D与点F重合，进而猜想．
【问题解决】
(1)小亮对上面的猜想进行了证明，下面是部分证明过程：
证明：四边形是矩形，
∴．
由折叠可知，，．
∴．
∴．
请你补全余下的证明过程．
【结论应用】
(2)的度数为________度，的值为_________；
(3)在图①的条件下，点P在线段上，且，点Q在线段上，连结、，如图②，设，则的最小值为_________．（用含a的代数式表示）
24．（2021·湖北荆州·统考中考真题）在矩形中，，，是对角线上不与点，重合的一点，过作于，将沿翻折得到，点在射线上，连接．
（1）如图1，若点的对称点落在上，，延长交于，连接．
①求证：；
②求．
（2）如图2，若点的对称点落在延长线上，，判断与是否全等，并说明理由．
专题18 矩形折叠问题
模型的概述：已知矩形的长与宽，利用勾股定理、相似三角形及翻折的性质，求各线段边长。
解题方法：不找以折痕为边长的直角三角形，利用未知数表示其它直角三角形三边，通过勾股定理/相似三角形知识求解。
问题：根据已知信息，求翻折后各边长。
模型一： 思路：

模型二： 思路：

模型三： 思路：

尝试借助一线三垂直知识利用相似的方法求解
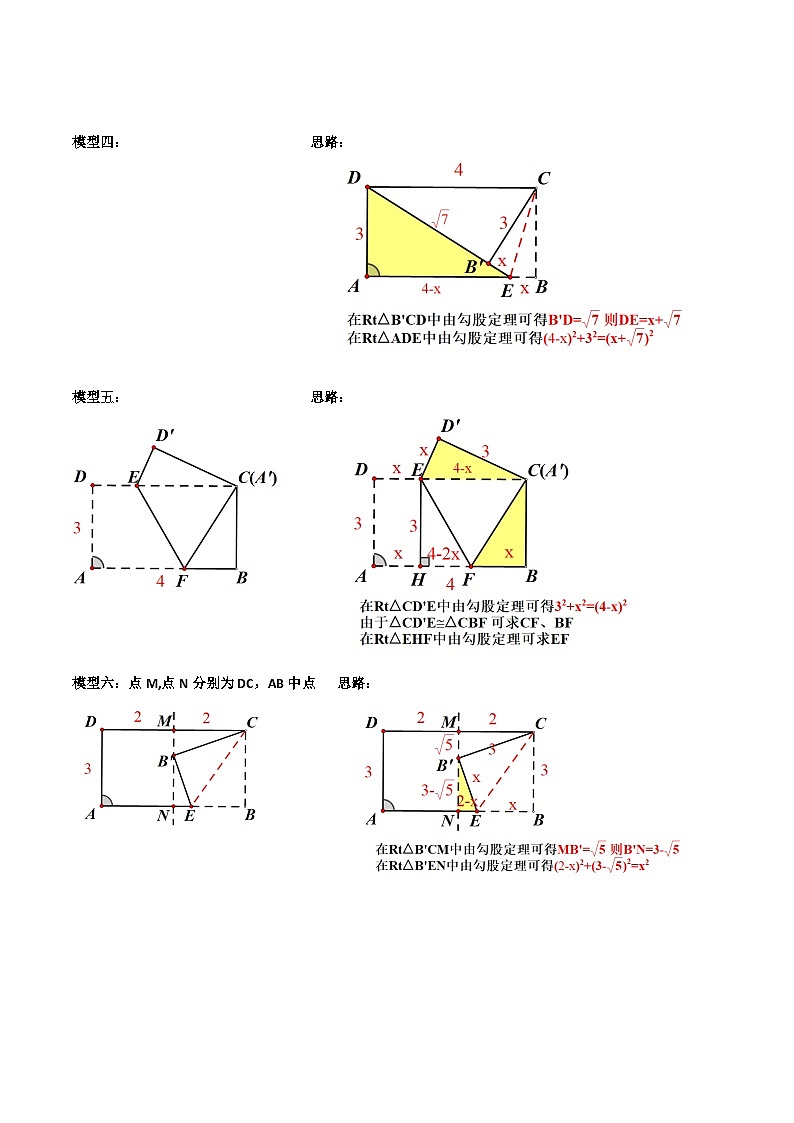
模型四： 思路：
模型五： 思路：
模型六：点M,点N分别为DC，AB中点 思路：

模型七：点A’为BC中点 思路： 过点F作FH⊥AE，垂足为点H
设AE=A’E=x，则BE=8-x
由勾股定理解得x=174 ∴BE=154
由于△EBA’∽△A’CG∽△FD’G
∴A’G=3415 CG=1615 GD’=2615
DF=D’F=AH=134 HE=1 EF=17
【培优过关练】
1．（2022秋·山东青岛·九年级统考期末）如图，在正方形中，，点、分别在边、上，若将四边形沿折叠，点恰好落在边上，则的长度为（ ）
A．B．C．D．
【答案】B
【分析】根据翻折的性质和正方形及勾股定理的有关性质求解．
【详解】解：在正方形中，，，，
，
，
，
，
，
又，，
，，
，
故选：B．
【点睛】本题考查了翻折及正方形的性质，勾股定理的应用是解题的关键．
2．（2022秋·江苏徐州·九年级校考阶段练习）如图，在矩形纸片中，点E在边上，沿着折叠使点A落在边上的点F处，若，，则的长为（ ）
A．1B．2C．D．
【答案】A
【分析】先根据折叠的性质和正切的定义得出，再证明，最后利用相似三角形的性质得出结论．
【详解】解：由折叠可知，，
∴，
∴，
∵，
∴，，
∴，
∴，
∴，
∵，
∴，
故选：A．
【点睛】本题考查了矩形中的折叠问题，涉及三角函数，相似三角形判定与性质等知识，解题的关键是证明．
3．（2022秋·福建泉州·九年级福建省惠安第一中学校联考期中）如图，在平面直角坐标系中，矩形的边在x轴上，边在y轴上，点B的坐标为，将矩形沿对角线折叠，使点B落在D点的位置，且交y轴交于点E，则点D的坐标是（ ）
A．（）B．（，2）C．（）D．
【答案】D
【分析】过D作于F，根据折叠可以证明，然后利用全等三角形的性质得到，设，那么，利用勾股定理即可求出m，然后利用已知条件可以证明，而，接着利用相似三角形的性质即可求出、的长度，也就求出了点D的坐标．
【详解】如图，过D作于F，
∵点B的坐标为，
∴，
根据折叠可知，
而
∴，
∴，
设，那么，
在中，，
∴，
解得，
∵，
∴，
∴
而，
∴，
∴，
即，
∴，
∴，
∴D的坐标为，
故选：D．
【点睛】此题主要考查了图形的折叠问题，也考查了坐标与图形的性质，解题的关键是把握折叠的隐含条件，利用隐含条件得到全等三角形和相似三角形，然后利用它们的性质即可解决问题．
4．（2023春·广东广州·九年级专题练习）如图，矩形纸片中，，，折叠纸片使落在对角线上，折痕为，点的对应点为，那么的长为（ ）
A．1B．C．D．2
【答案】C
【分析】首先设，由矩形纸片中，，，可求得的长，又由折叠的性质，可求得的长，然后由勾股定理可得方程：，解此方程即可解决问题．
【详解】解：设，
∵四边形是矩形，
∴，
∵，，
∴，
由折叠的性质可得：，，，
∴，，，
∵在中，，
∴，
解得：，
∴．
故选：C．
【点睛】此题考查了折叠的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想与方程思想的应用．
5．（2022秋·湖南邵阳·九年级校联考期中）如图，在矩形纸片中，，点E在上，将沿折叠，点恰落在边上的点F处；点在上，将△ABG沿折叠，点恰落在线段上的点处，有下列结论：①；②；③四边形的面积等于；④．其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【分析】利用折叠性质得，，，，，则可得到，于是可对①进行判断；在中利用勾股定理计算出，则，设，利用勾股定理得到，得到，于是可对④进行判断；接着证明，于是可对②进行判断；根据可对③进行判断．
【详解】解：∵沿折叠，点恰落在边上的点处；点在上，
将沿折叠，点恰落在线段上的点处，
∴，，，，，，
∴，所以①正确；
在中， ，
∴，
设，则，
在中，
∵，
∴，
解得，
∴，
∴，所以④正确；
在中，，设，则
∴
解得
∴
∵，，
∴
．所以③不正确．
∵，
∴
∴故②正确
故选：C．
【点睛】本题考查了矩形的折叠问题，勾股定理，相似三角形的性质与判定，掌握以上知识是解题的关键．
6．（2022秋·广东梅州·九年级校考阶段练习）如图，在矩形中，，，点E为的中点，将沿折叠，使点B落在矩形内点F处，连接，则的长为（ ）
A．B．C．D．
【答案】D
【分析】连接，根据三角形的面积公式求出，得到，根据直角三角形的判定得到，根据勾股定理求出答案．
【详解】解：连接，交于H，
∵，点E为的中点，
∴，
又∵，
∴，
由折叠知，（对应点的连线必垂直于对称轴），
∴，
则，
∵，
∴，，
∵，
∴，
∴，
故选：D．
【点睛】本题考查的是翻折变换的性质和矩形的性质，掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．
7．（2022秋·广西贵港·九年级统考期中）如图，在矩形纸片中，，，M是上的点，且，将矩形纸片沿过点M的直线折叠，使点D落在上的点P处，点C落在点处，折痕为，当与线段交于点H时，则线段的长是（ ）
A．3B．C．4D．
【答案】B
【分析】连接，证明即可得到，证明，得出，然后列出关于x的方程，解方程即可．
【详解】解：连接，如图所示：
∵矩形纸片中，，，
∴，，
∵，
∴，
根据折叠可知，，，，
∴，
∴，
∵，
∴，
∴，
∵，，
∴，
∴，
设，则，
∵，
∴，
解得：，
∴，故B正确．
故选：B．
【点睛】本题考查矩形的折叠问题，解题的关键是看到隐藏条件，证明三角形全等，学会利用翻折不变性解决问题．
8．（2022秋·山东枣庄·九年级校考期中）如图，边长为2的正方形的对角线与交于点O，将正方形沿直线折叠，点C落在对角线上的点E处，折痕交于点M，则（ ）
A．B．C．D．
【答案】B
【分析】根据题意先求，再求，进而根据的线段比例关系，即可求出的长．
【详解】解：如图，连接，
∵四边形是正方形，
∴，，
∴，
由折叠的性质可知，，
∴，
∴，
∴是等腰直角三角形，
∴，
∵，
∴，
∴，
即，
∴．
故选：B．
【点睛】本题主要考查图形的翻折，熟练掌握图形翻折的性质，正方形的性质，等腰直角三角形的性质及相似三角形的判定和性质是解题的关键．
9．（2022·辽宁营口·统考中考真题）如图，在矩形中，点M在边上，把沿直线折叠，使点B落在边上的点E处，连接，过点B作，垂足为F，若，则线段的长为（ ）
A．B．C．D．
【答案】A
【分析】先证明△BFC≌△CDE，可得DE=CF=2，再用勾股定理求得CE=，从而可得AD=BC=，最后求得AE的长．
【详解】解：∵四边形ABCD是矩形，
∴BC=AD，∠ABC=∠D=90°，AD∥BC，
∴∠DEC=∠FCB，
∵，
∴∠BFC=∠CDE，
∵把沿直线折叠，使点B落在边上的点E处，
∴BC=EC，
在△BFC与△CDE中，
∴△BFC≌△CDE（AAS），
∴DE=CF=2，
∴，
∴AD=BC=CE=，
∴AE=AD-DE=，
故选：A．
【点睛】本题考查了矩形的性质、全等三角形的判定和性质、折叠的性质，勾股定理的应用，解决本题的关键是熟练掌握矩形中的折叠问题．
10．（2022·贵州毕节·统考中考真题）矩形纸片中，E为的中点，连接，将沿折叠得到，连接．若，，则的长是（ ）
A．3B．C．D．
【答案】D
【分析】连接BF交AE于点G，根据对称的性质，可得AE垂直平分BF，BE=FE，BG=FG=，根据E为BC中点，可证BE=CE=EF，通过等边对等角可证明∠BFC=90°，利用勾股定理求出AE，再利用三角函数（或相似）求出BF，则根据计算即可．
【详解】连接BF，与AE相交于点G，如图，
∵将沿折叠得到
∴与关于AE对称
∴AE垂直平分BF，BE=FE，BG=FG=
∵点E是BC中点
∴BE=CE=DF=
∴
∵
∴
∴
∵BE=CE=DF
∴∠EBF=∠EFB，∠EFC=∠ECF
∴∠BFC=∠EFB+∠EFC=
∴
故选 D
【点睛】本题考查了折叠对称的性质，熟练运用对称性质证明相关线段相等是解题的关键．
11．（2022·四川宜宾·统考中考真题）如图，在矩形纸片ABCD中，，，将沿BD折叠到位置，DE交AB于点F，则的值为（ ）
A．B．C．D．
【答案】C
【分析】先根据矩形的性质和折叠的性质，利用“AAS”证明，得出，，设，则，根据勾股定理列出关于x的方程，解方程得出x的值，最后根据余弦函数的定义求出结果即可．
【详解】解：∵四边形ABCD为矩形，
∴CD=AB=5，AB=BC=3，，
根据折叠可知，，，，
∴在△AFD和△EFB中，
∴（AAS），
∴，，
设，则，
在中，，
即，
解得：，则，
∴，故C正确．
故选：C．
【点睛】本题主要考查了矩形的折叠问题，三角形全等的判定和性质，勾股定理，三角函数的定义，根据题意证明，是解题的关键．
12．（2022·浙江湖州·统考中考真题）如图，已知BD是矩形ABCD的对角线，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BE，DF．将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在对角线BD上的点G，H处，连结GF．则下列结论不正确的是（ ）
A．BD＝10B．HG＝2C．D．GF⊥BC
【答案】D
【分析】根据矩形的性质以及勾股定理即可判断A，根据折叠的性质即可求得，进而判断B，根据折叠的性质可得，进而判断C选项，根据勾股定理求得的长，根据平行线线段成比例，可判断D选项
【详解】BD是矩形ABCD的对角线，AB＝6，BC＝8，
故A选项正确，
将△ABE沿BE翻折，将△DCF沿DF翻折，
，
,
故B选项正确，
,
∴EG∥HF，
故C正确
设，则，
，
即
，同理可得
若
则
，
，
不平行，
即不垂直，
故D不正确．
故选D
【点睛】本题考查了折叠的性质，矩形的性质，勾股定理，平行线分线段成比例，掌握以上知识是解题的关键．
13．（2022·江苏连云港·统考中考真题）如图，将矩形ABCD沿着GE、EC、GF翻折，使得点A、B、D恰好都落在点O处，且点G、O、C在同一条直线上，同时点E、O、F在另一条直线上．小炜同学得出以下结论：①GF∥EC；②AB=AD；③GE=DF；④OC=2OF；⑤△COF∽△CEG．其中正确的是（ ）
A．①②③B．①③④C．①④⑤D．②③④
【答案】B
【分析】由折叠的性质知∠FGE=90°，∠GEC=90°，点G为AD的中点，点E为AB的中点，设AD=BC=2a，AB=CD=2b，在Rt△CDG中，由勾股定理求得b=，然后利用勾股定理再求得DF=FO=，据此求解即可．
【详解】解：根据折叠的性质知∠DGF=∠OGF，∠AGE=∠OGE，
∴∠FGE=∠OGF+∠OGE=(∠DGO+∠AGO) =90°，
同理∠GEC=90°，
∴∠FGE+∠GEC=180°
∴GF∥EC；故①正确；
根据折叠的性质知DG=GO，GA=GO，
∴DG=GO=GA，即点G为AD的中点，
同理可得点E为AB的中点，
设AD=BC=2a，AB=CD=2b，则DG=GO=GA=a，OC=BC=2a，AE=BE=OE=b，
∴GC=3a，
在Rt△CDG中，CG2=DG2+CD2，
即(3a)2=a2+(2b)2，
∴b=，
∴AB=2=AD，故②不正确；
设DF=FO=x，则FC=2b-x，
在Rt△COF中，CF2=OF2+OC2，
即(2b-x)2=x2+(2a)2，
∴x==，即DF=FO=，
GE=a，
∴，
∴GE=DF；故③正确；
∴，
∴OC=2OF；故④正确；
∵∠FCO与∠GCE不一定相等，
∴△COF∽△CEG不成立，故⑤不正确；
综上，正确的有①③④，
故选：B．
【点睛】本题主要考查了折叠问题，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．
14．（2021·广西来宾·统考中考真题）如图，矩形纸片，，点，分别在，上，把纸片如图沿折叠，点，的对应点分别为，，连接并延长交线段于点，则的值为（ ）
A．B．C．D．
【答案】A
【分析】根据折叠性质则可得出是的垂直平分线，则由直角三角形性质及矩形性质可得∠AEO=∠AGD，∠FHE＝∠D＝90°，根据相似三角形判定推出△EFH∽△GAD，再利用矩形判定及性质证得FH＝AB，即可求得结果．
【详解】解：如图，过点F作FH⊥AD于点H，
∵点，的对应点分别为，，
∴，，
∴EF是AA＇的垂直平分线．
∴∠AOE=90°．
∵四边形是矩形，
∴∠BAD＝∠B＝∠D＝90°．
∴∠OAE＋∠AEO=∠OAE＋∠AGD，
∴∠AEO=∠AGD．
∵FH⊥AD，
∴∠FHE＝∠D＝90°．
∴△EFH∽△GAD．
∴．
∵∠AHF＝∠BAD＝∠B＝90°，
∴四边形ABFH是矩形．
∴FH＝AB．
∴；
故选：A．
【点睛】本题考查了矩形的折叠问题，掌握折叠的性质、矩形及相似三角形的判定与性质是解题的关键．
15．（2011·吉林长春·中考真题）如图，矩形纸片ABCD中，已知AD =8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )
A．3B．4
C．5D．6
【答案】D
【分析】先根据矩形的特点求出BC的长，再由翻折变换的性质得出△CEF是直角三角形，利用勾股定理即可求出CF的长，再在△ABC中利用勾股定理即可求出AB的长．
【详解】解：∵四边形ABCD是矩形，AD=8，
∴BC=8，
∵△AEF是△AEB翻折而成，
∴BE=EF=3，AB=AF，△CEF是直角三角形，
∴CE=8﹣3=5，
在Rt△CEF中，CF==4，
设AB=x，
在Rt△ABC中，AC2=AB2+BC2，
即（x+4）2=x2+82，
解得x=6，
故选：D．
【点睛】本题考查了翻折变换（折叠问题），勾股定理，解题的关键是利用勾股定理建立等式求解．
16．（2020·广东深圳·统考中考真题）如图，矩形纸片ABCD中，AB=6，BC=12．将纸片折叠，使点B落在边AD的延长线上的点G处，折痕为EF，点E、F分别在边AD和边BC上．连接BG，交CD于点K,FG交CD于点H．给出以下结论：①EF⊥BG；②GE=GF；③△GDK和△GKH的面积相等；④当点F与点C重合时，∠DEF=75°．其中正确的结论共有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【分析】由折叠的性质可得四边形EBFG是菱形从而判断①②正确;由角平分线定理即可判断DG≠GH,由此推出③错误;根据F、C重合时的性质,可得∠AEB=30°,进而算出④正确．
【详解】
连接BE,由折叠可知BO=GO，
∵EG//BF，
∴∠EGO=∠FBO，
又∵∠EOG=∠FOB，
∴△EOG≌△FOB(ASA) ，
∴EG=BF，
∴四边形EBFG是平行四边形，
由折叠可知BE=EG，
则四边形EBFG为菱形，
故EF⊥BG，GE=GF，
∴①②正确；
∵四边形EBFG为菱形，
∴KG平分∠DGH，
∴,DG≠GH，
∴ S△GDK≠S△GKH,故③错误；
当点F与点C重合时，BE=BF=BC=12=2AB，
∴∠AEB＝30°，，故④正确．
综合，正确的为①②④．
故选C．
【点睛】本题考查矩形的性质,菱形的判断,折叠的性质,关键在于结合图形对线段和角度进行转换．
17．（2020·内蒙古呼和浩特·中考真题）如图，把某矩形纸片沿，折叠（点E、H在边上，点F，G在边上），使点B和点C落在边上同一点P处，A点的对称点为、D点的对称点为，若，的面积 为8，的面积为2，则矩形的长为（ ）
A．B．C．D．
【答案】D
【分析】设AB=CD=x，由翻折可知：PA′=AB=x，PD′=CD=x，因为△A′EP的面积为4，△D′PH的面积为1，推出D′H＝x，由S△D′PH=D′P·D′H=A′P·D′H，可解得x=2，分别求出PE和PH，从而得出AD的长.
【详解】解：∵四边形ABC是矩形，
∴AB=CD，AD=BC，
设AB=CD=x，
由翻折可知：PA′=AB=x，PD′=CD=x，
∵△A′EP的面积为8，△D′PH的面积为2，
又∵，∠A′PF=∠D′PG=90°，
∴∠A′P D′=90°，则∠A′PE+∠D′PH=90°，
∴∠A′PE=∠D′HP，
∴△A′EP∽△D′PH，
∴A′P2：D′H2=8：2，
∴A′P：D′H=2：1，
∵A′P=x，
∴D′H=x，
∵S△D′PH=D′P·D′H=A′P·D′H，即，
∴x=2（负根舍弃），
∴AB=CD=2，D′H=DH=，D′P=A′P=CD=2，A′E=2D′P=4，
∴PE=，PH=，
∴AD==，
故选D.
【点睛】本题考查翻折变换，矩形的性质，勾股定理，相似三角形的判定和性质等知识，解题的关键是学会利用参数解决问题，属于中考填空题中的压轴题．
18．如图，矩形纸片ABCD，AB=4，BC=3，点P在BC边上，将△CDP沿DP折叠，点C落在点E处，PE、DE分别交AB于点O、F，且OP=OF，则cs∠ADF的值为（ ）
A．B．C．D．
【答案】C
【分析】根据折叠的性质可得出DC=DE、CP=EP，由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP（AAS），根据全等三角形的性质可得出OE=OB、EF=BP，设EF=x，则BP=x、DF=4﹣x、BF=PC=3﹣x，进而可得出AF=1+x，在Rt△DAF中，利用勾股定理可求出x的值，再利用余弦的定义即可求出cs∠ADF的值．
【详解】根据折叠，可知：△DCP≌△DEP，
∴DC=DE=4，CP=EP．
在△OEF和△OBP中，，
∴△OEF≌△OBP（AAS），
∴OE=OB，EF=BP．
设EF=x，则BP=x，DF=DE﹣EF=4﹣x，
又∵BF=OB+OF=OE+OP=PE=PC，PC=BC﹣BP=3﹣x，
∴AF=AB﹣BF=1+x．
在Rt△DAF中，AF2+AD2=DF2，即（1+x）2+32=（4﹣x）2，
解得：x=，
∴DF=4﹣x=，
∴cs∠ADF=，
故选C．
【点睛】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形，利用勾股定理结合AF=1+x，求出AF的长度是解题的关键．
19．（2022·山东泰安·统考中考真题）如图，四边形为正方形，点E是的中点，将正方形沿折叠，得到点B的对应点为点F，延长交线段于点P，若，则的长度为___________．
【答案】2
【分析】连接AP，根据正方形的性质和翻折的性质证明Rt△AFP≌Rt△ADP（HL），可得PF＝PD，设PF＝PD＝x，则CP＝CD−PD＝6−x，EP＝EF＋FP＝3＋x，然后根据勾股定理即可解决问题．
【详解】解：连接AP，如图所示，
∵四边形ABCD为正方形，
∴AB＝BC＝AD＝6，∠B＝∠C＝∠D＝90°，
∵点E是BC的中点，
∴BE＝CE＝AB＝3，
由翻折可知：AF＝AB，EF＝BE＝3，∠AFE＝∠B＝90°，
∴AD＝AF，∠AFP＝∠D＝90°，
在Rt△AFP和Rt△ADP中，
，
∴Rt△AFP≌Rt△ADP（HL），
∴PF＝PD，
设PF＝PD＝x，则CP＝CD−PD＝6−x，EP＝EF＋FP＝3＋x，
在Rt△PEC中，根据勾股定理得：EP2＝EC2＋CP2，
∴（3＋x）2＝32＋（6−x）2，解得x＝2，则DP的长度为2，
故答案为：2．
【点睛】本题考查了翻折变换，正方形的性质，勾股定理，解决本题的关键是掌握翻折的性质．
20．（2022·贵州黔东南·统考中考真题）如图，折叠边长为4cm的正方形纸片，折痕是，点落在点处，分别延长、交于点、，若点是边的中点，则______cm．
【答案】##
【分析】根据折叠的性质可得DE=DC=4，EM=CM=2，连接DF，设FE=x，由勾股定理得BF，DF，从而求出x的值，得出FB，再证明，利用相似三角形对应边成比例可求出FG．
【详解】解：连接如图，
∵四边形ABCD是正方形，
∴
∵点M为BC的中点，
∴
由折叠得，∠
∴∠，
设则有
∴
又在中，，
∵
∴
∴
在中，
∴
解得，（舍去）
∴
∴
∴
∵∠
∴∠
∴∠
又∠
∴△
∴即
∴
故答案为：
【点睛】本题主要考查了正方形的性质，折叠的性质，勾股定理，相似三角形的判定与性质，正确作出辅助线是解答本题的关键．
21．（2022·浙江丽水·统考中考真题）如图，将矩形纸片折叠，使点B与点D重合，点A落在点P处，折痕为．
(1)求证：；
(2)若，求的长．
【答案】(1)证明见解析
(2)cm
【分析】（1）利用ASA证明即可；
（2）过点E作EG⊥BC交于点G，求出FG的长，设AE=xcm，用x表示出DE的长，在Rt△PED中，由勾股定理求得答案．
【详解】（1）∵四边形ABCD是矩形，
∴AB=CD，∠A=∠B=∠ADC=∠C=90°，
由折叠知，AB=PD，∠A=∠P，∠B=∠PDF=90°，
∴PD=CD，∠P=∠C，∠PDF =∠ADC，
∴∠PDF-∠EDF=∠ADC-∠EDF,
∴∠PDE=∠CDF，
在△PDE和△CDF中，
,
∴（ASA）；
（2）如图，过点E作EG⊥BC交于点G，
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm，
又∵EF=5cm，∴cm,
设AE=xcm，
∴EP=xcm，
由知，EP=CF=xcm，
∴DE=GC=GF+FC=3+x，
在Rt△PED中，,
即，
解得，，
∴BC=BG+GC= (cm）．
【点睛】本题考查了翻折变换，矩形的性质，勾股定理，全等三角形的判定和性质，根据翻折变换的性质将问题转化到直角三角形中利用勾股定理是解题的关键．
22．（2022·河南·统考中考真题）综合与实践
综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．

(1)操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM．
根据以上操作，当点M在EF上时，写出图1中一个30°的角：______．
(2)迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．
①如图2，当点M在EF上时，∠MBQ＝______°，∠CBQ＝______°；
②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由．
(3)拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm时，直接写出AP的长．
【答案】(1)或或或
(2)①15，15；②，理由见解析
(3)cm或
【分析】（1）根据折叠的性质，得，结合矩形的性质得，进而可得；
（2）根据折叠的性质，可证，即可求解；
（3）由（2）可得，分两种情况：当点Q在点F的下方时，当点Q在点F的上方时，设分别表示出PD，DQ，PQ，由勾股定理即可求解．
（1）
解：
，sin∠BME=
（2）
∵四边形ABCD是正方形
∴AB=BC，∠A=∠ABC=∠C=90°
由折叠性质得：AB=BM，∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
②
（3）
当点Q在点F的下方时，如图，
，DQ=DF+FQ=4+1=5(cm)
由（2）可知，
设
，
即
解得：
∴；
当点Q在点F的上方时，如图，
cm，DQ =3cm，
由（2）可知，
设
，
即
解得：
∴．
【点睛】本题主要考查矩形与折叠，正方形的性质、勾股定理、三角形的全等，掌握相关知识并灵活应用是解题的关键．
23．（2022·吉林长春·统考中考真题）【探索发现】在一次折纸活动中，小亮同学选用了常见的A4纸，如图①，矩形为它的示意图．他查找了A4纸的相关资料，根据资料显示得出图①中．他先将A4纸沿过点A的直线折叠，使点B落在上，点B的对应点为点E，折痕为；再沿过点F的直线折叠，使点C落在上，点C的对应点为点H，折痕为；然后连结，沿所在的直线再次折叠，发现点D与点F重合，进而猜想．
【问题解决】
(1)小亮对上面的猜想进行了证明，下面是部分证明过程：
证明：四边形是矩形，
∴．
由折叠可知，，．
∴．
∴．
请你补全余下的证明过程．
【结论应用】
(2)的度数为________度，的值为_________；
(3)在图①的条件下，点P在线段上，且，点Q在线段上，连结、，如图②，设，则的最小值为_________．（用含a的代数式表示）
【答案】(1)见解析
(2)22.5°，
(3)
【分析】（1）根据折叠的性质可得AD=AF，，由HL可证明结论；
（2）根据折叠的性质可得 证明是等腰直角三角形，可求出GF的长，从而可得结论 ；
（3）根据题意可知点F与点D关于AG对称，连接PD，则PD为PQ+FQ的最小值，过点P作PR⊥AD，求出PR=AR=，求出DR，根据勾腰定理可得结论．
【详解】（1）证明：四边形是矩形，
∴．
由折叠可知，，．
∴．
∴．
由折叠得，，
∴
∴
又AD=AF，AG=AG
∴
（2）由折叠得，∠
又∠
∴∠
由得，∠
∠
又∠
∴∠
∴∠
∴
设则
∴
∴
∴
（3）如图，连接
∵
∴AG是FD的垂直平分线，即点F与点D关于AG轴对称，
连接PD交AG于点Q，则PQ+FQ的最小值为PD的长；
过点P作交AD于点R，
∵∠
∴∠
∴
又
∴
∴
在中，
∴
∴的最小值为
【点睛】本题主要考查了折叠的性质，全等三角形的判定与性质，最短路径问题，矩形的性质以及勾股定理等知识，正确作出辅助线构造直角三角形是解答本题的关键．
24．（2021·湖北荆州·统考中考真题）在矩形中，，，是对角线上不与点，重合的一点，过作于，将沿翻折得到，点在射线上，连接．
（1）如图1，若点的对称点落在上，，延长交于，连接．
①求证：；
②求．
（2）如图2，若点的对称点落在延长线上，，判断与是否全等，并说明理由．
【答案】（1）①见解析；②；（2）不全等，理由见解析
【分析】（1）①先根据同角的余角相等得出∠DCG=∠AGH，再根据两角对应相等，两三角形相似即可得出结论；
②设EF=x，先证得△AEF△ADC，得出===，再结合折叠的性质得出AE=EG=2x，
AG=4x，AH=2EF=2x，再由△CDG△GAH，得出比例式==，求出EF的长，从而得出的值，即可得出答案；
（2）先根据两角对应相等，两三角形相似得出△AEF△ACG，得出比例式=，得出EF=，
AE=，AF=，从而判定与是否全等．
【详解】（1）①在矩形ABCD中，∠BAD=∠D=90°
∴∠DCG+∠DGC=90°
又∵∠FGC=90°
∴∠AGH+∠DGC=90°
∴∠DCG=∠AGH
∴△CDG△GAH
②设EF=x
∵△AEF沿EF折叠得到△GEF
∴AE=EG
∵EF⊥AD
∴∠AEF=90°=∠D
∴EF//CD//AB
∴△AEF△ADC
∴=
∴===
∴AE=EG=2x
∴AG=4x
∵AE=EG，EF//AB
∴==
∴AH=2EF=2x
∵△CDG△GAH
∴==
∴==
∴x=
∴==
∵∠FCG=90°
∴tan∠GHC==
（2）不全等 理由如下：
在矩形ABCD中，AC===
由②可知：AE=2EF
∴AF==EF
由折叠可知，AG=2AE=4EF，AF=GF
∵∠AEF=∠GCF，∠FAE=∠GAC
∴△AEF△ACG
∴=
∴=
∴EF=
∴AE=，AF=
∴FC=AC-AF=2-=
∴AEFC，EFFC
∴不全等
【点睛】本题考查了矩形的性质，翻折变换，相似三角形的判定和性质，三角函数等知识，得出AE=2EF是解题的关键．