沪教版八年级数学下册期中期末满分冲刺卷特训06期中选填题(上海精选归纳65题，20.1-22.2)(原卷版+解析)

这是一份沪教版八年级数学下册期中期末满分冲刺卷特训06期中选填题(上海精选归纳65题，20.1-22.2)(原卷版+解析)，共46页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。
1．（2023春·上海·八年级专题练习）以下函数中，属于一次函数的是（ ）
A．y＝B．y＝
C．y＝c（c为常数）D．y＝kx+b（k、b为常数）
2．（2022秋·上海静安·八年级新中初级中学校考期末）如果一次函数的图象经过原点，则的值为（ ）
A．0或1B．1C．0D．不存在
3．（2021·上海·九年级专题练习）若函数是一次函数，则m的值为（ ）
A．B．1C．D．2
4．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）已知函数，当时，的值为（ ）
A．6B．3C．D．
5．（2023春·八年级单元测试）已知一次函数的图象与直线平行，且过点，那么一次函数的表达式是（ ）
A．B．C．D．
6．（2023春·八年级单元测试）在一次函数中，y随x的增大而减小，那么常数m的取值范围是（ ）
A．；B．；C．；D．．
7．（2023春·上海宝山·八年级校考阶段练习）已知一次函数，那么下列结论正确的是（ ）
A．图像必经过点B．图像经过第一．二．三象限
C．当时，D．的值随的值增大而增大
8．（2022秋·上海青浦·八年级校考期末）在直角坐标平面内，一次函数的图像如图所示，那么下列说法正确的是（ ）
A．当时，B．方程 的解是
C．当时，D．不等式 的解集是
9．（2022春·上海普陀·九年级校考期中）已知直线ykxb经过第一、三、四象限，那么直线ybxk一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
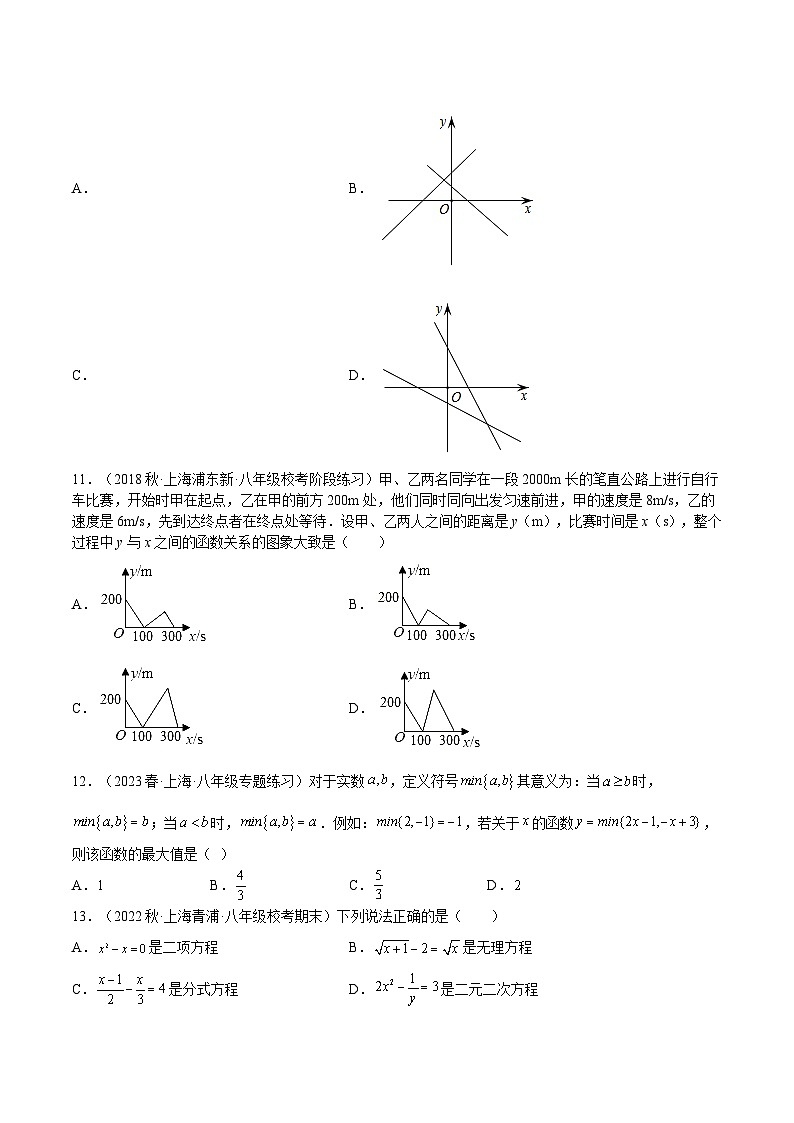
10．（2023春·八年级单元测试）将一次函数与的图像画在同一坐标系中，正确的是（ ）
A．B．
C．D．
11．（2018秋·上海浦东新·八年级校考阶段练习）甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛，开始时甲在起点，乙在甲的前方200m处，他们同时同向出发匀速前进，甲的速度是8m/s，乙的速度是6m/s，先到达终点者在终点处等待．设甲、乙两人之间的距离是y（m），比赛时间是x（s），整个过程中y与x之间的函数关系的图象大致是（ ）
A．B．
C．D．
12．（2023春·上海·八年级专题练习）对于实数，定义符号其意义为：当时，；当时，．例如：，若关于的函数，则该函数的最大值是（ ）
A．B．C．D．
13．（2022秋·上海青浦·八年级校考期末）下列说法正确的是（ ）
A．是二项方程B．是无理方程
C．是分式方程D．是二元二次方程
14．（2022春·上海·八年级专题练习）若关于x的分式方程无解，则k的值为（ ）
A．B．－1C．1D．
15．（2022·上海·上海市娄山中学校考二模）下列方程中，有实数根的方程是（ ）
A．B．
C．D．
16．（2022春·上海浦东新·八年级校考期中）小明在解方程组的过程中，以下说法错误的是（ ）
A．可得，再用代入消元法解
B．令，，可用换元法将原方程组化为关于、的二元一次方程组
C．由得，再代入，可得一个关于的分式方程，亦可求解
D．经检验：是方程组的一组解
17．（2023春·八年级单元测试）用换元法解分式方程，如果设，那么原方程化为关于的整式方程是（ ）
A．B．
C．D．
18．（2022春·上海·八年级校考阶段练习）下列方程组中是二元二次方程组的是（ ）
A．B．C．D．
19．（2020春·八年级校考课时练习）张老师和李老师同时从学校出发，步行15千米去书店购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x千米，根据题意，所列的方程是（ ）
A．B．
C．D．
20．（2022春·上海·八年级专题练习）方程组的所有整数解的组数是（ ）
A．2B．3C．4D．5
21．（2022春·上海普陀·八年级校考期中）一个凸多边形的内角中最多有几个锐角( )
A．个B．个C．个D．个
22．（2023春·上海·八年级专题练习）如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（ ）
A．六边形B．五边形C．四边形D．三角形
23．（2023春·上海·八年级专题练习）一个多边形边数每增加1条时，其内角和（ ）
A．增加B．增加C．不变D．不能确定
24．（2022春·上海嘉定·八年级校考期中）下列命题中不正确的是（ ）
A．两组对角分别相等的四边形是平行四边形
B．两组对边分别相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形
D．对角线相等的四边形是平行四边形
25．（2022春·上海·八年级校考期中）已知四边形ABCD，有以下四个条件：①；②；③；④．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（ ）
A．6种B．5种C．4种D．3种
26．（2022春·上海奉贤·八年级校考期中）如图平行四边形的对角线与相交于点，，，周长为16，那么对角线的长等于（ ）
A．4B．5C．6D．8
27．（2023春·上海·八年级专题练习）平面直角坐标系中，平行四边形三个顶点坐标分别为，则顶点B的坐标为（ ）
A．B．C．D．
28．（2021春·上海徐汇·八年级上海市民办华育中学校考期中）如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1，S2，S3，S4，则一定成立的是（ ）
A．S1+S2＞S3+S4B．S1+S2=S3+S4C．S1+S2＜S3+S4D．S1+S3=S2+S4
二、填空题
29．（2022春·上海·九年级上海市西南模范中学校考阶段练习）如果直线y＝ax＋b经过点（1，3），那么a＋b＝______．
30．（2023春·上海·八年级专题练习）已知函数是关于x的一次函数，则______．
31．（2022春·上海·八年级专题练习）以下函数中y是x的一次函数的有_________个．
①；②；③；④；⑤；⑥．
32．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若一次函数中随的增大而减小，则的取值范围是______．
33．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线可以由直线沿着轴向______（填“上”“下”）平移______个单位得到．
34．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线与轴、y轴分别交于点A、B两点，则原点到直线的距离为___________．
35．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若关于的一次函数的截距为1，则的值为___________．
36．（2023春·上海宝山·八年级校考阶段练习）如果直线经过点，那么不等式的解集为_________．
37．（2023春·上海宝山·八年级校考阶段练习）直线关于轴对称的直线的解析式为______．
38．（2023春·上海宝山·八年级校考阶段练习）函数的图象与轴．轴围成的三角形面积为______．
39．（2023春·上海·八年级专题练习）如图，在平面直角坐标系中，直线与坐标轴交于，两点，于点，是线段上的一个动点，连接，将线段绕点逆时针旋转，得到线段，连接，则线段的最小值为______．
40．（2023春·上海·八年级专题练习）、两地相距50千米，小张骑自行车从地到地，车速为13千米/小时，骑了小时后，小张离地千米，那么关于的函数解析式是___．
41．（2022秋·上海·八年级专题练习）上海磁悬浮列车在一次运行中速度V（千米/小时）关于时间t（分钟）的函数图象如图，回答下列问题．
（1）列车共运行了___分钟
（2）列车开动后，第3分钟的速度是___千米/小时．
（3）列车的速度从0千米/小时加速到300千米/小时，共用了___分钟．
（4）列车从___分钟开始减速．
42．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）写出一个由一个二元一次方程和一个二元二次方程组成的方程组，使它的解是；，那么该方程组可以是__________．
43．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）已知关于x的方程有增根，那么__________．
44．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）用换元法解分式方程时，如果设，那么可将原方程变形后表示为关于y的一元二次方程一般形式：___________．
45．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）无理方程：在实数范围内___________．（填写“有解”或“无解”）
46．（2023春·上海宝山·八年级校考阶段练习）若方程：有解，则的取值范围是______．
47．（2022秋·上海静安·八年级新中初级中学校考期末）写出一个由二元一次方程和一个二元二次方程组成的二元二次方程组___________，使它的解是和．
48．（2023春·八年级单元测试）方程组的解只有一组，则的取值范围是______．
49．（2022春·上海·九年级校考期中）方程的解是____________．
50．（2022春·上海浦东新·八年级校考期中）方程的根是______．
51．（2023春·八年级单元测试）如果方程无实数解，那么的取值范围是______．
52．（2022春·上海·八年级校考期中）某工人要完成个零件，起初机器出现故障，每分钟比原计划少加工个零件，加工个零件后，换了一台新机器，每分钟比原计划多加工个零件．已知用新机器加工零件的时间比前面用旧机器加工零件的时间少分钟，设原计划每分钟加工个零件，则可列方程为：______．
53．（2022春·上海·八年级专题练习）某次列车平均提速vkm/h．用相同的时间，列车提速前行驶skm．提速后比提速前多行驶50km．设提速前列车的平均速度是xkm/h．根据题意分别列出下列四个方程：①；②；③；④．则其中正确的方程有_________．
54．（2022秋·上海虹口·八年级上外附中校考阶段练习）小明在解方程时采用了下面的方法：由
，
又有，可得，将这两式相加可得，
将两边平方可解得，经检验是原方程的解．
请你学习小明的方法，解决下列问题：
（1）已知，则的值为___________．
（2）解方程，得方程的解为___________．
55．（2022秋·上海嘉定·九年级统考阶段练习）如果某个多边形的内角和为1260°，那么它的边数是 _____．
56．（2022秋·上海静安·八年级新中初级中学校考期末）如果一个多边形的内角和为，那么过这个多边形的一个顶点可作___________条对角线．
57．（2019春·上海·八年级上海市娄山中学校考阶段练习）在平行四边形中，的平分线把分成长度是3，4的两部分，则平行四边形的周长是_____．
58．（2023秋·上海青浦·八年级校考期末）如图，平行四边形中，，垂足分别是E、F，，则平行四边形的周长为_______．
59．（2023秋·上海青浦·八年级校考期末）如图所示，在平行四边形中，cm，cm，的平分线交于点，交的延长线于点，则___cm．
60．（2023春·上海·八年级专题练习）若一个平行四边形的一个内角平分线把一条边分成和两条线段，则该平行四边形的周长为__________．
61．（2022春·上海·八年级校考期中）如图，在平行四边形中，于点，于点，，且，则平行四边形的周长为______．
62．（2021春·上海·八年级上海市进才中学北校校考期中）如图，中，，于，交于，若，则的大小是________．
63．（2021春·上海杨浦·八年级校考期中）如图，在平行四边形中，对角线的垂直平分线交于点，连接．若平行四边形的周长为20cm，则的周长为______cm．
64．（2022春·上海杨浦·八年级校考期末）如图， 的对角线与相交于点，将翻折使点与点重合，点落在点，已知（是锐角），那么的度数为______．（用的代数式表示）
65．（2023春·上海·八年级专题练习）在平行四边形中，和交于点O，，，如果将沿直线翻折后，点B落在点E处，那么的面积等于________．
特训06 期中选填题（上海精选归纳65题，20.1-22.2）
一、单选题
1．（2023春·上海·八年级专题练习）以下函数中，属于一次函数的是（ ）
A．y＝B．y＝
C．y＝c（c为常数）D．y＝kx+b（k、b为常数）
【答案】A
【分析】根据一次函数的概念：形如（均是常数），对四个选项逐一进行判断即可．
【解析】A、中，，是一次函数，故该选项符合题意；
B、是反比例函数，故该选项不符合题意；
C、（c是常数）是常函数，故该选项不符合题意；
D、当时，就不是一次函数，故该选项不符合题意；
故选：A．
【点睛】此题考查一次函数的概念，熟练掌握一次函数的概念是解此题的关键．
2．（2022秋·上海静安·八年级新中初级中学校考期末）如果一次函数的图象经过原点，则的值为（ ）
A．0或1B．1C．0D．不存在
【答案】B
【分析】将原点坐标代入，得到关于m的一元二次方程，再根据一次项系数不能为0为方根的解进行取舍即可．
【解析】解：将原点坐标代入，
可得，
解得，，
是一次函数，
，
，
故选B．
【点睛】本题考查一次函数的图象和性质，以及解一元二次方程，解题的关键是注意解析式中一次项的系数不能为0．
3．（2021·上海·九年级专题练习）若函数是一次函数，则m的值为（ ）
A．B．1C．D．2
【答案】C
【分析】根据一次函数的定义列式计算即可得解．
【解析】解：根据题意得，且，
解得且，
所以，．
故选：C．
【点睛】本题主要考查了一次函数的定义，一次函数的定义条件是：、为常数，，自变量次数为1．
4．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）已知函数，当时，的值为（ ）
A．6B．3C．D．
【答案】C
【分析】由题意得：函数，令，得到，整理得，两边同时平方，最后解一元二次方程即可求出的值，但最后将求出的值代入检验．
【解析】已知函数，
当时，
∴，
∴，
∴，
∴，
∴，
∴，
∴，，
经检验：时不符合题意，故舍去，
∴当时，的值为，
故选：C
【点睛】本题主要考查已知函数值，求自变量的值，解一元二次方程，熟练掌握相关知识点是解题的关键．
5．（2023春·八年级单元测试）已知一次函数的图象与直线平行，且过点，那么一次函数的表达式是（ ）
A．B．C．D．
【答案】B
【分析】根据两直线平行，结合题意即可设一次函数解析式为，再利用待定系数法求解即可．
【解析】解：∵一次函数的图象与直线平行，
∴可设一次函数解析式为：．
将点代入，得：，
解得：，
∴一次函数的表达式为：．
故选B．
【点睛】考查了一次函数图象平行的问题．解题关键是明确一次函数图象平行时k的值不变，再利用待定系数法求解析式．
6．（2023春·八年级单元测试）在一次函数中，y随x的增大而减小，那么常数m的取值范围是（ ）
A．；B．；C．；D．．
【答案】D
【分析】先根据一次函数的增减性得出关于的不等式，求出的取值范围即可．
【解析】解：∵在一次函数中，随的增大而减小，
∴，解得．
故选：D．
【点睛】本题主要考查了一次函数的性质．一次函数，当时，随的增大而减小；当时，随的增大而增大．
7．（2023春·上海宝山·八年级校考阶段练习）已知一次函数，那么下列结论正确的是（ ）
A．图像必经过点B．图像经过第一．二．三象限
C．当时，D．的值随的值增大而增大
【答案】C
【分析】根据一次函数的图像上点的特征对选项A进行判断；根据一次函数的性质对选项B、D进行判断；利用时，函数图像的特征对选项C进行判断；即可得出答案．
【解析】解：A、当时，，则点不在函数图像上，故此选项不符合题意；
B、，
此函数的图像经过第一、二、四象限，故此选项不符合题意；
C、∵函数与轴的交点横坐标是，函数函数值随的增大而减小，
∴交点的右边，
即：当时，，故此选项符合题意；
D、，
y随x的增大而减小，故此选项不符合题意；
故选：C．
【点睛】此题考查了一次函数的图像与性质，熟练掌握一次函数的图像与性质、学会用数形结合的思想方法是解此题的关键．
8．（2022秋·上海青浦·八年级校考期末）在直角坐标平面内，一次函数的图像如图所示，那么下列说法正确的是（ ）
A．当时，B．方程 的解是
C．当时，D．不等式 的解集是
【答案】C
【分析】根据函数的图象直接进行解答即可．
【解析】解：由函数的图象可知，
当时，，A选项错误，不符合题意；
方程 的解是，B选项错误，不符合题意；
当时，，故C正确，符合题意；
不等式 的解集是，故D错误，不符合题意．
故选：C．
【点睛】本题考查的是一次函数的图象，利用数形结合求解是解答此题的关键．
9．（2022春·上海普陀·九年级校考期中）已知直线ykxb经过第一、三、四象限，那么直线ybxk一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【分析】根据直线y=kx+b经过第一，三，四象限，可以判断k、b的正负，根据一次函数图象的性质，从而可以判断直线y=bx+k经过哪几个象限，不经过哪个象限．
【解析】解：∵直线y=kx+b经过第一，三，四象限，
∴k>0，b