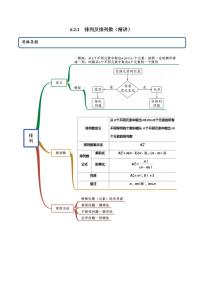
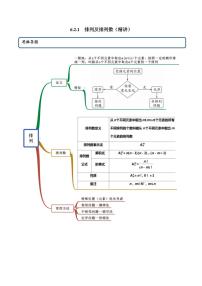
人教A版 (2019)选择性必修 第三册6.2 排列与组合优秀学案及答案
展开1.理解排列、排列数的概念.
2.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.
3.能熟练地运用排列知识解决一些有关排列的实际问题.
4.通过实例,体验数学知识的形成与发展,学会分析问题、解决问题的方式,培养解决实际问题的能力.
重点难点
1.重点:
理解排列的定义及排列数的计算;
将具体问题抽象为将元素排成一列的问题,解决问题并归纳出共同特点,进而得到排列的概念;
在运用排列解决实际问题时,将实际问题抽象成排列问题.
2.难点:
将实际问题中的具体对象抽象为元素,得到排列的定义;
运用排列解决计算问题.
课前预习 自主梳理
知识点一 排列的定义
排列:一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
知识点二 排列相同的条件
两个排列相同的充要条件:
(1)两个排列的元素完全相同.
(2)元素的排列顺序也相同.
(1)排列中“一定顺序”的含义是什么?
提示:一定顺序就是指排列中的元素与位置有关,当位置不同时排列也就不同.
(2)排列定义中的两个要素是什么?
提示:一是“取出不同的元素”,二是“将元素按一定顺序排列”.
3.排列中元素所满足的两个特性
(1)无重复性:从n个不同元素中取出m(m≤n)个不同的元素,否则不是排列问题.
(2)有序性:安排这m个元素时是有顺序的,有序的就是排列,无序的不是排列.检验它是否有顺序的依据是变换元素的位置,看结果是否发生变化,有变化就是有顺序,无变化就是无顺序.
(1)每一个排列中元素的位置是确定的吗?
提示:是,元素在排列中的位置不同排列也就不同.
(2)同一个排列中,同一个元素能重复出现吗?
提示:由排列的定义知,在同一个排列中不能重复出现同一个元素.
自主检测
1.判断正误,正确的画“√”,错误的画“×”.
123与321是相同的排列.( )
同一个排列中,同一个元素不能重复出现.( )
在一个排列中,若交换两个元素的位置,则该排列不发生变化.( )
从4个不同元素中任取3个元素,只要元素相同得到的就是相同的排列.( )
【答案】(1)×(2)√(3)×(4)×
2.,,,,五名学生按任意次序站成一排,其中和不相邻,则不同的排法种数为( )
A.72B.36C.18D.64
【答案】A
【分析】先将其余三人全排列,利用插空法求解.
【详解】解:先将其余三人全排列,共有种情况,
再将和插空,共有种情况,
所以共有种情况,
故选:A.
3.下列问题是排列问题的是( )
A.从8名同学中选取2名去参加知识竞赛,共有多少种不同的选取方法?
B.10个人互相通信一次,共写了多少封信?
C.平面上有5个点,任意三点不共线,这5个点最多可确定多少条直线?
D.从1,2,3,4四个数字中,任选两个相乘,其结果共有多少种?
【答案】B
【分析】排列问题是与顺序问题有关的问题,只有B选项涉及顺序,由此可得结果.
【详解】对于A,名同学中选取名,不涉及顺序问题,不是排列问题,A错误;
对于B,个人互相通信,涉及到顺序问题,是排列问题,B正确;
对于C,个点中任取点,不涉及顺序问题,不是排列问题,C错误;
对于D,个数字中任取个,根据乘法交换律知结果不涉及顺序,不是排列问题,D错误.
故选:B.
4.6个停车位置,有3辆汽车需要停放,若要使3个空位连在一起,则停放的方法种数为( )
A.B.C.D.
【答案】D
【分析】将3个空位看成一个整体,与原有的3辆汽车全排列即可.
【详解】将3个空位看成一个整体,问题转化为4个元素全排列问题,即.
【点睛】相邻元素捆绑法:就是在解决对于某几个元素要求相邻问题时,可整体考虑将相邻元素视为一个大元素.
5.名男同学、名女学生和位老师站成一排拍照合影,要求位老师必须站正中间,队伍左右两端不能同时是一男学生与一女学生,则总共有( )种排法.
A.B.C.D.
【答案】C
【分析】先把6个学生按要求排列,要求两端都是男生或都是女生,再从中间空位中插入两个老师,根据分步计数原理求得结果.
【详解】解:根据题意,先把6个学生排列;
①若两端都是男生,则有种排法,
②若两端都是女生,则有种排法,
再从中间空位中插入两个老师,有种排法.
根据分步计数原理,满足条件的排列共有种排法,
故选:C.
新课导学
学习探究
环节一 创设情境,引入课题
1.复习两个计数原理
找两名同学表述两个计数原理的内容,回顾利用两个 计数原理解决问题的步骤.
2.在上节教材第9页例8的解答中我们看到,用分步 乘法计数原理解决问题时,因做了一些重复性工作而显得 烦琐.能否对这类计数问题给出一种简捷的方法呢?
问题1从甲、乙、丙3名同学中选出2名参加项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
师生活动:教师提出问题:你能用上节课我们学习的计数原理解决这一问题吗?
教师可以通过提问,让学生表述用计数原理解决这一问题的过程.
学生用计数原理解答:
此时,要完成的一件事是“选出2名同学参加活动,1名同学参加上午的活动,另1名同学参加下午的活动”,可以分两个步骤:
第1步,确定参加上午活动的同学,从3人中任选1人,有3种选法;
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种选法.
根据分步乘法计数原理,不同的选法种数为
.
追问:你能列举出各种不同的选法吗?
教师让学生动手列举,引导学生用树状图列举,并指1名学生在黑板上列举.
这6种不同的选法如图6.2-1所示.
追问:如果把上面问题中被选出的对象叫做元素,那么你会表述问题1吗?
学生试着用自己的语言进行表述,教师进一步对学生的表述进行规范指导.
如果把上面问题中被取出的对象叫做元素,那么问题可叙述为:
从3个不同的元素a,b,c中任意取出2个,并按一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
ab,ac,ba,bc,cb,ca.
不同的排列方法种数为
.
问题1中的“顺序”是什么?
设计意图:通过问题1,采用问题串的形式,引导学生 深入思考,为抽象出排列的概念作准备.
环节二 观察分析,感知概念
问题2从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
师生活动:教师提出问题:你能用计数原理分析解决这一问题吗?解决这一问题需要用分类加法计数原理还是分步乘 法计数原理?
学生完成解答后,教师指名学生回答.
显然,从4个数字中,每次取出3个,按“百位、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.
可以分三个步骤来解决这个问题:
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种方法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种方法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位的数字只能从余下的2个数字中去取,有2种方法.
根据分步乘法计数原理,从1,2,3,4这4个不同的数字中,每次取出3个数字,按“百位、十位、个位”的顺序排成一列,不同的排法种数为
.
因而共可得到24个不同的三位数,
追问:你能用树状图列出所有不同的三位数吗?
学生列举,教师用投影仪展示学生的列举情况(如下图所示).
由此可写出所有的三位数:
123,124,132,134,142,143,
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
同样,问题2可以归结为:
从4个不同的元素中任意取出3个,并按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
不同的排列方法种数为
问题2中的“顺序”是什么?
设计意图:在这一问题中元素的个数增加到了 4个, 取其中3个,增加了问题的复杂度,但本问题的解决过程 和问题1是一样的.让学生再次经历用计数原理解决这一 问题的过程,为形成排列的概念做好了准备.
环节三 抽象概括,形成概念
问题3:上述问题1,2的共同特点是什么?你能将它们推广到一般情形吗?
师生活动:教师提出上述问题,让学生思考、交流、 讨论.
指名学生展示讨论交流的结果,教师进一步规范学生 的表述,从而归纳出排列的定义;
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列(arrangement).
追问:如何判断两个排列是否相同?
根据排列的定义,两个排列相同的充要条件是:两个排列的元素完全相同,且元素的排列顺序也相同.例如,在问题1中,“甲乙”与“甲丙”的元素不完全相同,它们是不同的排列;“甲乙”与“乙甲”虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.又如,在问题2中,123与134的元素不完全相同,它们是不同的排列;123与132虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.
设计意图:通过对上面的两个问题进行数学抽象,在 学生充分思考、交流、讨论的基础上得出排列的定义,让学 生经历这一过程,提升学生的数学抽象核心素养.
环节四 辨析理解 深化概念
例1 某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
师生活动:
教师提出问题:这一问题是不是排列问题?你能根据 排列的定义分析这一问题吗?
学生分析、思考.
教师在学生思考的同时,可以给出提示:
分析:每组任意2支队之间进行的1场比赛,可以看作是从该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.
追问:如何利用计数原理求出比赛的场数?
解:可以先从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队.按分步乘法计数原理,每组进行的比赛场数为
.
设计意图:引导学生用排列的概念去思考分析这一问 题,加深对排列概念的理解与认识,提升学生用所学知识 分析问题、解决问题的能力.
环节五 概念应用,巩固内化
例2(1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
师生活动:
教师引导学生分析:3名同学每人从5盘不同的菜中 取1盘菜,可看作是从这5盘菜中任取3盘,放在3个位 置(给3名同学)的一个排列;而3名同学每人从食堂窗 口的5种菜中选1种,每人都有5种选法,不能看成一个 排列.
分析:3名同学每人从5盘不同的菜中取1盘菜,可看作是从这5盘菜中任取3盘,放在3个位置(给3名同学)的一个排列;而3名同学每人从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列.
解:(1)可以先从这5盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为
.
(2)可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从5种菜中选1种,也有5种选法;最后让同学丙从5种菜中选1种,同样有5种选法.按分步乘法计数原理,不同的选法种数为
.
环节六 归纳总结,反思提升
1.用以下问题引导学生归纳总结:
(1)如何抽象出排列的定义?
(2)如何判断一个计数问题是否是排列问题?
(3)如何列举所有的排列?
排列的定义:顺序性.
“树形图”法列举排列.
排列的简单应用.
2. 在解决问题时,用到了哪些数学思想?数形结合.
3.常见误区:排列的定义不明确.
设计意图:通过问题引导学生回顾总结本节课学习的 内容,让学生加深对新知的理解.
环节七目标检测,作业布置
完成教材:第16〜17页练习第1,2,3题.
设计意图:通过练习检查学生对排列概念的理解情况.
备用练习
1.旅游体验师小李受某网站邀请,决定在甲、乙、丙、丁这四个景区进行体验式旅游已知他不能最先去甲景区旅游,不能最后去乙景区和丁景区旅游,则他可选的旅游路线的条数为( )
A.24B.18C.16D.10
【答案】D
【分析】小李可选的旅游路线分两种情况:① 最后去甲景区旅游,可的路线有条;② 不最后去甲景区旅游,可选路线有条.
【详解】解:小李可选的旅游路线分两种情况:① 最后去甲景区旅游,则可选的路线有条;② 不最后去甲景区旅游,则可选的路线有条.
所以小李可选的旅游路线的条数为.
故选:D.
2.在某场新冠肺炎疫情视频会议中,甲、乙、丙、丁四位疫情防控专家轮流发言,其中甲必须排在前两位,丙、丁必须排在一起,则四位专家的不同发言顺序共有( )
A.12种B.8种C.6种D.4种
【答案】C
【分析】先排甲,再将丙、丁捆绑在一起当一个元素排,再排乙.
【详解】当甲排在第一位时,共有种发言顺序,
当甲排在第二位时,共有种发言顺序,
所以一共有种不同的发言顺序.
故选:C.
3.从6名员工中选出3人分别从事教育、培训、管理三项不同的工作,则选派方案共有( )
A.60种B.80种C.100种D.120种
【答案】D
【分析】利用排列的定义直接列式求解.
【详解】从6名员工中选出3人分别从事教育、培训、管理三项不同的工作,则选派方案共(种).
故选:D.
4.随着北京冬奥会的开幕,吉祥物“冰墩墩”火遍国内外,现有3个完全相同的“冰墩墩”,甲、乙、丙、丁、戊5位运动员要与这3个“冰墩墩”站成一排拍照留念,则有且只有2个“冰墩墩”相邻的排队方法数为( ).
A.3600B.1440C.720D.480
【答案】A
【分析】根据题意,由“捆绑法”与“插空法”,代入计算,即可得到结果.
【详解】因为3个“冰墩墩”完全相同,将其中两个“冰墩墩”捆绑,记为元素,另外一个“冰墩墩”记为元素,
先将甲、乙、丙、丁、戊5位运动员全排列,即,
然后将元素插入这五位运动员所形成的空中,即,
则不同的排法种数为.
故选:A
5.一排个座位坐了个三口之家,若每家人坐在一起,则不同的坐法种数为( ).
A.B.C.D.
【答案】C
【分析】由已知,现将每一个家庭内部成员进行排列,每个家庭为种排法,那么三个家庭则是种排法,然后再对三组家庭整体进行排序,即种排法,最后组合在一起即可.
【详解】有已知题意可知,
先将每一个家庭的内部成员进行去排列,共有种排法,
将每个三口之家看成一个元素,三个整体元素进行排列,共有种排法,
所以不同的坐法种数为.
故选:.
高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合导学案: 这是一份高中数学人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000352_t4/?tag_id=42" target="_blank">6.2 排列与组合导学案</a>,文件包含第02讲排列教师版-高二数学同步精品讲义人教A版选择性必修第三册doc、第02讲排列学生版-高二数学同步精品讲义人教A版选择性必修第三册doc等2份学案配套教学资源,其中学案共43页, 欢迎下载使用。
数学选择性必修 第三册第七章 随机变量及其分布7.5 正态分布学案: 这是一份数学选择性必修 第三册<a href="/sx/tb_c4000360_t4/?tag_id=42" target="_blank">第七章 随机变量及其分布7.5 正态分布学案</a>,共16页。
数学选择性必修 第三册6.2 排列与组合导学案: 这是一份数学选择性必修 第三册<a href="/sx/tb_c4000352_t4/?tag_id=42" target="_blank">6.2 排列与组合导学案</a>,共11页。学案主要包含了排列的相关概念,排列数与排列数公式等内容,欢迎下载使用。