数学第六章 计数原理6.2 排列与组合精品学案设计

这是一份数学第六章 计数原理6.2 排列与组合精品学案设计，文件包含人教A版数学高二选择性必修第三册622排列数导学案原卷版docx、人教A版数学高二选择性必修第三册622排列数导学案解析版docx等2份学案配套教学资源，其中学案共21页， 欢迎下载使用。

.能在排列基础上给出排列数的定义和表示，并能区别排列与排列数.
.通过利用计数原理分析和解决具体的排列问题，得到排列数公式，并能利用公式求具体 问题的排列数.
重点难点
重点：排列数公式.
难点：排列数公式的应用.
课前预习 自主梳理
知识点一 排列数的定义
从n个不同元素中取出m(m≤n)个元素的 ，叫做从n个不同元素中取出m个元素的排列数，用符号Aeq \\al(m,n)表示.
思考 排列与排列数相同吗？
答案 排列数是元素排列的个数，两者显然不同．
知识点二 排列数公式及全排列
1．排列数公式的两种形式
(1)Aeq \\al(m,n)＝ ，其中m，n∈N*，并且m≤n.
(2)Aeq \\al(m,n)＝ .
2．全排列
将n个不同的元素全部取出的排列数，等于正整数1到n的连乘积，叫做n的阶乘，用n！表示，于是n个元素的全排列数公式可以写成：Aeq \\al(n,n)＝n! ，另外规定，0！＝1.
4.排列数及排列数公式
(1)“得到从n个不同的元素中取出m个元素的一个排列”的含义是什么?
提示:“得到从n个不同元素中取出m个元素的一个排列”,包含两个方面:①从n个不同元素中取出m个元素;②按照一定顺序排列.
(2)排列与排列数有何不同?
提示:排列与排列数是两个不同的概念,“排列”是指从n个不同元素中取出m个元素按照一定顺序排成一列,是一种排法;“排列数”是指从n个不同元素中取出m个元素所得不同排列的个数,是一个数,用 QUOTE ??? Aeq \\al(m,n)表示.
自主检测
1.判断正误，正确的画“√”，错误的画“×”．
(1)由于排列数的阶乘式是一个分式,所以其化简的结果不一定是整数.( )
(2)在排列的问题中,总体中的元素可以有重复.( )
(3)用1,2,3这三个数字组成无重复数字的三位数.123与321是不相同的排列.( )
(4)若 QUOTE ??? QUOTE ??? Aeq \\al(m,n)=10×9×8×7×6,则n=10,m=6.( )
2.如果，那么，分别为（ ）
A．15，10B．15，9C．15，6D．16，10
3.等于（ ）
A．B．C．D．
4.某铁路所有车站共发行132种普通客票，则这段铁路共有车站数是
A．8B．12C．16D．24
5.，则m等于（ ）
A．3B．4C．5D．6
新课导学
学习探究
环节一 创设情境，引入课题
问题1：在6.2.1节问题1、问题2中，我们是根据计数原理和列举数数的方式得到排列的个数.但随着元素个数的增加，这样的方法就越来越烦琐了.是否有计算排列个数的公式，从而能便捷地求出排列的个数？
前面给出了排列的定义，下面探究计算排列个数的公式．
我们把从n个不同元素中取出个元素的所有不同排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号表示．
符号中的A是英文arrangement（排列）的第一个字母．
师:请你分别算出上一节问题1、问题2的排列数，并用排列数符号表示.
例如，前面问题1是求从3个不同元素中取出2个元素的排列数，表示为．已经算得
．
问题2是求从4个不同元素中取出3个元素的排列数，表示为．已经算得
．
师:请你思考一下，排列数的符号与计算结果之间有什么联系？
环节二 观察分析，感知概念
问题2：从个不同元素中取出个元素的排列数是多少?
追问（1）：我们已经知道，6.2.1节问题1的排列数,问题2的排列数,那么如何 求排列数?
可以先从特殊情况开始探究，例如求排列数．根据前面的求解经验，可以这样考虑：
假定有排好顺序的两个空位，如图6.2-3所示，从n个不同元素中取出2个元素去填空，一个空位填上一个元素，每一种填法就得到一个排列；反之，任何一种排列总可以由这种填法得到．因此，所有不同填法的种数就是排列数．
现在来计算有多少种填法．完成“填空”这件事可以分为两个步骤完成：
第1步，填第1个位置的元素，可以从这个不同元素中任选1个，有种选法；
第2步，填第2个位置的元素，可以从剩下的个元素中任选1个，有种选法．
根据分步乘法计数原理，2个空位的填法种数为
．
追问（2）：如何求排列数?
同理，求排列数可以按依次填3个空位来考虑，有
．
追问(3)：你能类比求排列数和的方法，求排列数吗？
一般地，求排列数可以按依次填个空位来考虑：
假定有排好顺序的个空位，如图6.2-4所示，从个不同元素中取出个元素去填空，一个空位填上一个元素，每一种填法就对应一个排列．因此，所有不同填法的种数就是排列数．
填空可以分为个步骤完成：
第1步，从个不同元素中任选1个填在第1位，有种选法；
第2步，从剩下的个元素中任选1个填在第2位，有种选法；
第3步，从剩下的个元素中任选1个填在第3位，有种选法；
……
第步，从剩下的个元素中任选1个填在第位，有种选法．
根据分步乘法计数原理，个空位的填法种数为
．
这样，我们就得到公式
这里，，并且．这个公式叫做排列数公式．
环节三 抽象概括，形成概念
你能说一下排列数公式的特点吗？
问题3：上述排列数公式有什么特点？使用公式需要注意什么？
根据排列数公式，我们就能方便地计算出从n个不同元素中取出个元素的所有排列的个数．例如，
，
．
特别地，我们把个不同的元素全部取出的一个排列，叫做个元素的一个全排列．
这时，排列数公式中，即有
．
也就是说，将个不同的元素全部取出的排列数，等于正整数1到的连乘积．正整数1到的连乘积，叫做的阶乘，用表示．于是，个元素的全排列数公式可以写成
另外，我们规定，．
环节四 辨析理解 深化概念
例3 计算：（1）；（2）；（3）；（4）．
思考
由例3可以看到，；，即．观察这两个结果，从中你发现它们的共性了吗?
追问：观察这两个结果，从中发现它们的共性了吗？能否将它进行推广？
事实上，
因此，排列数公式还可以写成
．
环节五 概念应用，巩固内化
例4用0～9这10个数字，可以组成多少个没有重复数字的三位数?
对于例4这类计数问题，从不同的角度就有不同的解题方法．解法1根据百位数字不能是0的要求，按分步乘法计数原理完成从10个数中取出3个数组成没有重复数字的三位数这件事；解法2是以0是否出现以及出现的位置为标准，按分类加法计数原理完成这件事；解法3是一种间接法，先求出从10个数中取出3个数的排列数，然后减去其中百位是0的排列数(不是三位数的个数)，就得到没有重复数字的三位数的个数．
从上述问题的解答过程可以看到，引入排列的概念，归纳出排列数公式，我们就能便捷地求解“从个不同元素中取出个元素的所有排列的个数”这类特殊的计数问题．
环节六 归纳总结,反思提升
1. 本节课学习的概念有哪些？
(1)排列数、排列数公式．
(2)全排列、阶乘、0！＝1.
(3)排列数的应用：排队问题(相邻、不相邻、定序等问题)．
2.教师引导学生回顾本节课学习的主要内容，并让学生回答下列问题：
排列与排列数是两个不同的概念，这两个概念有什么不同？
排列数公式是如何推导的？推导过程体现了什么样的数学思想与方法？
如何应用排列与排列数公式分析解决问题？
3. 在解决问题时，用到了哪些数学思想？
方法归纳：直接法、优先法、捆绑法、插空法、除阶乘法、间接法．
4．常见误区：忽视Aeq \\al(m,n)中“n，m∈N*”这个条件．
环节七目标检测，作业布置
教材第20页练习第3题，教材第26页习题6.2第1, 8题.
备用练习
1.．若，则（ ）
A．1B．6C．7D．8
2.（ ）
A．B．C．D．
3.用0，1，2，3，4可以组成的无重复数字的能被3整除的三位数的个数是（ ）
A．20B．24C．36D．48
4.计算：（1）；
（2）.
5.7名学生站成一排，若甲、乙相邻，但都不和丙相邻，则不同的排法种数是（ ）
A．480B．960C．720D．360
6.5人站成一排照相，甲不站在两端的站法有（ ）
A．24种B．72种C．96种D．120种
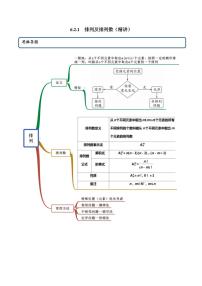
排列数定义
从n个不同元素中取出m(m≤n)个元素的所有 的个数,叫做从n个不同元素中取出m个元素的排列数
排列数表示法
Anm
全排列
n个不同元素全部取出的一个排列,叫做n个元素的一个全排列,且Ann=
阶乘
正整数1到n的连乘积,叫做n的阶乘,用n!表示
排列数公式
乘积式
Anm=n(n-1)(n-2)…(n-m+1)=n!(n-m)!
阶乘式
QUOTE ?!(?-?)! Anm=n!(n-m)!
性质
Ann= ,0!=
备注
n,m∈N*,m≤n