高中数学人教A版 (2019)选择性必修 第三册7.2 离散型随机变量及其分布列优秀一课一练

这是一份高中数学人教A版 (2019)选择性必修 第三册7.2 离散型随机变量及其分布列优秀一课一练，文件包含人教A版数学高二选择性必修第三册72离散型随机变量及其分布列分层作业原卷版docx、人教A版数学高二选择性必修第三册72离散型随机变量及其分布列分层作业解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

【夯实基础】
题型1随机变量的概念及分类
1.下列随机变量不是离散型随机变量的是
A．某景点一天的游客数ξ
B．某寻呼台一天内收到寻呼次数ξ
C．水文站观测到江水的水位数ξ
D．某收费站一天内通过的汽车车辆数ξ
【答案】C
【分析】根据离散型随机变量的概念，将不是离散的随机变量选出来，即是正确选项.
【详解】随着试验结果变化而变化的变量称为随机变量，所有取值可以一一列出的随机变量，称为离散型随机变量．对于C选项来说，由于水位数是属于实数，是一个连续的变量，不属于离散型随机变量.
【点睛】本小题主要考查离散型随机变量的概念，考查离散和随机这两个关键词的理解，属于基础题.
2.下面给出四个随机变量：①一高速公路上某收费站在1小时内经过的车辆数ξ是一个随机变量；②一个沿直线y＝x进行随机运动的质点，它在该直线上的位置η是一个随机变量；③某无线寻呼台1分钟内接到的寻呼次数ξ是一个随机变量；④1天内的温度η是一个随机变量.其中是离散型随机变量的为（ ）
A．①②B．③④C．①③D．②④
【答案】C
【分析】根据离散型随机变量的概念逐一判断即可.
【详解】①中经过的车辆数和③中寻呼次数都能列举出来，而②④中都不能列举出来，所以①③中的ξ是一个离散型随机变量.
故选：C.
3.甲、乙两人下象棋，赢了得3分，平局得1分，输了得0分，共下三局．用ξ表示甲的得分，则{ξ＝3}表示（ ）
A．甲赢三局
B．甲赢一局
C．甲、乙平局三次
D．甲赢一局输两局或甲、乙平局三次
【答案】D
【分析】根据题意，结合比赛得分规则，分析甲得3分的情况，即可求解.
【详解】由题意知，甲、乙两人下象棋，赢了得3分，平局得1分，输了得0分，
其中甲得3分，有两种情况：
甲赢一局输两局，甲得分为3分；
甲、乙平局三次，甲得分为3分.
所以{ξ＝3}表示甲赢一局输两局或甲、乙平局三次.
故选：D.
4.下列叙述中，是离散型随机变量的为（ ）
A．将一枚质地均匀的硬币掷五次，出现正面和反面向上的次数之和
B．某人早晨在车站等出租车的时间
C．连续不断地射击，首次命中目标所需要的次数
D．袋中有个黑球个红球，任取个，取得一个红球的可能性
【答案】C
【分析】根据离散型随机变量定义依次判断各个选项即可.
【详解】对于A，掷硬币只有正面向上和反面向上两种结果，则掷五次，出现正面和反面向上的次数之和为，是常量，A错误；
对于B，等出租车的事件是随机变量，但无法一一列出，不是离散型随机变量，B错误；
对于C，连续不断地射击，首次命中目标所需要的次数是有限个或可列举的无限多个，是离散型随机变量，C正确；
对于D，事件发生的可能性不是随机变量，D错误.
故选：C.
5.①某座大桥一天经过的车辆数为X；
②某通信公司官方客服一天内接听电话的总次数为X；
③一天之内的温度为X；
④一射手对目标进行射击，命中得1分，未命中得0分，用X表示射手在一次射击中的得分.
上述问题中的X是离散型随机变量的是（ ）
A．①②③B．①②④C．①③④D．②③④
【答案】B
【分析】根据离散型随机变量的定义：可列举性判断各项描述是否为离散随机变量即可.
【详解】①大桥一天经过的车辆数是可一一列举，
②客服一天内接听电话的总次数是可一一列举，
③一天之内的温度是连续型变量，
④一次射击中的得分是可一一列举，
由离散随机变量的定义知：①②④.
故选：B
题型2 离散型随机变量的判断
1.(多选题)下列变量：
①某机场候机室中一天的旅客数量为；
②某寻呼台一天内收到的寻呼次数为；
③某水电站观察到一天中长江的水位为；
④某立交桥一天内经过的车辆数为.
其中是离散型随机变量的是（ ）
A．①中的B．②中的
C．③中的D．④中的
【答案】ABD
【分析】利用离散型随机变量的概念，对选项逐一分析判断即可得解.
【详解】因为所有取值可以一一列出的随机变量为离散型随机变量，
而①②④中的随机变量的可能取值，我们都可以按一定的次序一一列出，
因此它们都是离散型随机变量；
而③中的可以取某一区间内的一切值，无法按一定次序一一列出，
因此它不是离散型随机变量.
故选：ABD.
2.下面给出四个随机变量，其中是离散型随机变量的为（ ）
A．高速公路某收费站在未来1小时内经过的车辆数X
B．一个沿直线进行随机运动的质点，它在该直线上的位置Y
C．某景点7月份每天接待的游客数量
D．某人一生中的身高X
【答案】AC
【分析】根据离散型随机变量的概念逐项分析判断.
【详解】对于选项A：收费站在未来1小时内经过的车辆数X有限，且可一一列出，是离散型随机变量，故A正确
对于选项C：某景点7月份每天接待的游客数量有限，且可一一列出，是离散型随机变量，故C正确；
对于选项B、D，都是某一范围内的任意实数，无法一一列出，不符合离散型随机变量的定义，故B、D错误．
故选：AC.
3.将一颗质地均匀的骰子掷两次，不能作为随机变量的是（ ）
A．两次掷出的点数之和
B．两次掷出的最大点数
C．第一次与第二次掷出的点数之差
D．两次掷出的点数
【答案】D
【分析】根据随机变量的定义，结合试验结果，逐项判定，即可求解.
【详解】A中，将一个骰子掷两次，两次掷出的点数之和是一个变量，且随试验结果的变化而变化，是一个随机变量．
B中，两次掷出的最大点数是一个变量，且随试验结果的变化而变化，是一个随机变量．
C中，第一次与第二次掷出的点数是一个变量，且随试验结果的变化而变化，之差也都是随机变量，
D中，两次掷出的点数不是一个变量，所以不是随机变量．
故选：D.
4.下列变量中，是离散型随机变量的是（ ）．
A．某机场明年5月1日运送乘客的数量
B．某办公室一天中接到电话的次数
C．某地警方明年5月1日到10月1日期间查处酒驾司机的人数
D．一瓶净含量为的果汁的容量
【答案】ABC
【分析】根据离散型随机变量的概念依次分析各选项即可得答案.
【详解】解：某机场明年5月1日运送乘客的数量可能为0，1，2，3，…，是随机变化的，而且可以一一列出，是离散型随机变量，故A正确；
某办公室一天中接到电话的次数可能为0，1，2，3，…，是随机变化的，而且可以一一列出，是离散型随机变量，故B正确；
某地警方明年5月1日到10月1日期间查处酒驾司机的人数可能为0，1，2，3，…，是随机变化的，而且可以一一列出，是离散型随机变量，故C正确；
果汁的容量在498mL～502mL之间波动，虽然是随机变量，但不能一一列出，不是离散型随机变量，故D错误．
故选：ABC．
5.袋中装有大小相同的5个球，分别标有1，2，3，4，5五个号码，现在在有放回的条件下依次取出两个球，设两个球的号码之和为随机变量ξ，则ξ所有可能取值的个数是（ ）
A．25B．10C．15D．9
【答案】D
【分析】根据有放回抽样，将号码之和可能的情况列举求解.
【详解】由题意得：两个球的号码之和可能为2，3，4，5，6，7，8，9，10，共9个.
故选：D
题型3用随机变量表示事件的结果
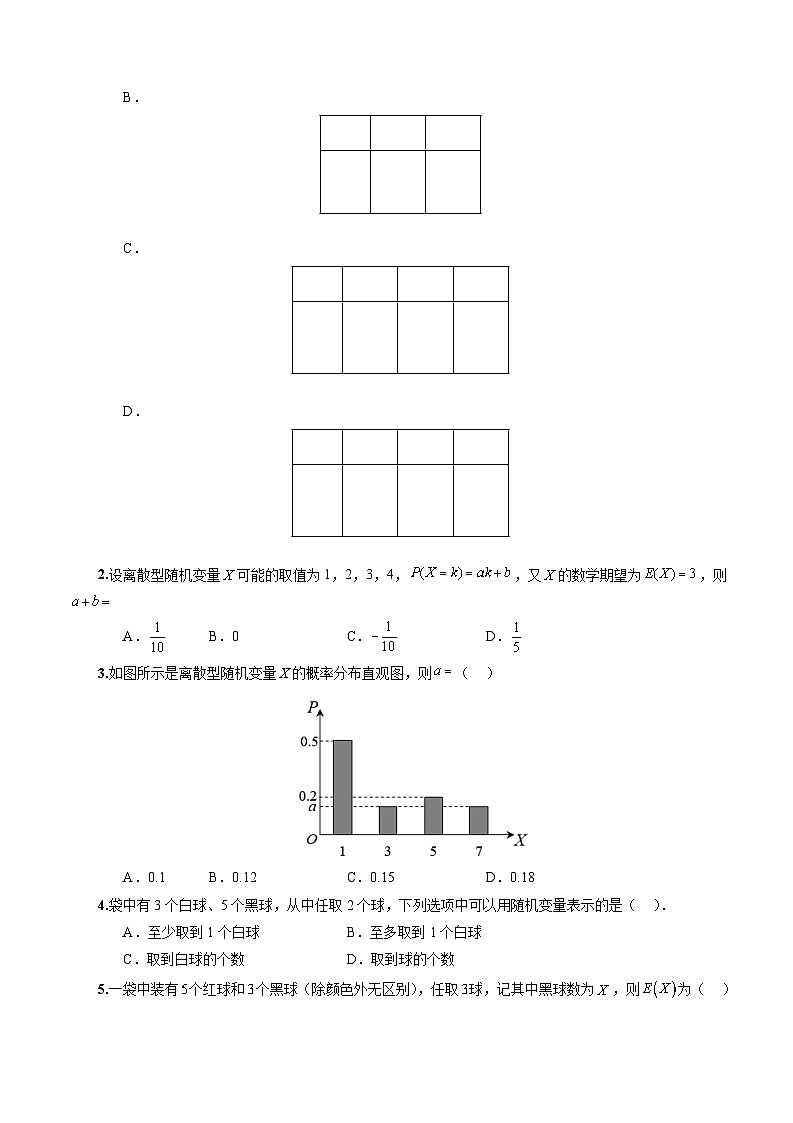
1.投掷两枚质地均匀的骰子，记偶数点朝上的骰子的个数为，则的分布列为（ ）
A．
B．
C．
D．
【答案】C
【分析】根据离散型随机变量的分布列，即可写出答案.
【详解】因为每枚骰子偶数点朝上的概率为，且相互独立，的取值可能为0，1，2.
，，，
所以的分布列为：
故选：C.
2.设离散型随机变量可能的取值为1，2，3，4，，又的数学期望为，则
A．B．0C．D．
【答案】A
【分析】将代入的表达式，利用概率之和为列方程，利用期望值列出第二个方程，联立方程组，可求解得的值.
【详解】依题意可的的分布列为
依题意得
，解得，故.所以选A.
【点睛】本小题主要考查离散型随机变量分布列，考查概率之和为，考查离散型随机变量的数学期望，还考查了方程的思想.属于基础题.
3.如图所示是离散型随机变量X的概率分布直观图，则（ ）
A．0.1B．0.12C．0.15D．0.18
【答案】C
【分析】根据所有随机变量的概率之和为1，列出方程，可求出答案.
【详解】由题意，解得．
故选：C．
4.袋中有3个白球、5个黑球，从中任取2个球，下列选项中可以用随机变量表示的是（ ）．
A．至少取到1个白球B．至多取到1个白球
C．取到白球的个数D．取到球的个数
【答案】C
【分析】由随机变量的含义可知.
【详解】选项A，B是随机事件；选项D是定值2；选项C可能的取值为0，1，2，可以用随机变量表示．
故选：C．
5.一袋中装有个红球和个黑球（除颜色外无区别），任取球，记其中黑球数为，则为（ ）
A．B．C．D．
【答案】A
【分析】由题意可知，随机变量的可能取值有、、、，计算出随机变量在不同取值下的概率，进而可求得随机变量的数学期望值.
【详解】由题意可知，随机变量的可能取值有、、、，
则，，，.
因此，随机变量的数学期望为.
故选：A.
【点睛】本题考查随机变量数学期望的计算，考查计算能力，属于基础题.
题型4求离散型随机变量的分布列
1.随机变量X的分布列如下，的值为（ ）
A．0.6B．0.7C．0.8D．0.9
【答案】C
【分析】首先根据分布列的性质，所有可能取值的概率之后等于1求得，再由求得答案即可.
【详解】解：随机变量X的分布列知：
，
.
故选：C
2.已知随机变量的分布列如表：
则实数（ ）
A．B．C．D．
【答案】A
【分析】根据随机变量的分布列的性质求解即可.
【详解】由题知，
解得．
故选：A
3.若离散型随机变量的分布列如下图所示．
则实数的值为（ ）
A．或B．C．D．或
【答案】C
【分析】根据给定条件，利用分布列的性质列式计算作答.
【详解】依题意，，解得，
所以实数的值为.
故选：C
4.．已知随机变量和，其中，且，若的分布列如下表，则的值为
A．B．C．D．
【答案】A
【分析】根据随机变量和的关系得到，概率和为1，联立方程组解得答案.
【详解】且，则
即

解得
故答案选A
【点睛】本题考查了随机变量的数学期望和概率，根据随机变量和的关系得到是解题的关键.
5.若离散型随机变量X的分布列为
则常数a的值为（ ）
A．B．C．或D．1或
【答案】A
【分析】根据可解出符合题意的的值.
【详解】由随机变量的分布列的性质知，
，
故选：A.
【点睛】本考查分布列的应用，属于简单题，运算量也不大，分布列的随机变量的概率要满足两个条件，一是每个概率都在区间，二是所有概率和为1.
题型5 分布列的性质及应用
1.设是离散型随机变量，则下列不一定能成为的概率分布列的一组概率的是（ ）
A．0.1，0.2，0.2，0.3，0.3
B．0.1，0.2，0.3，0.4
C．，（为实数）
D．，，，，（，）
【答案】C
【分析】利用分布列的性质判断.
【详解】对于A，概率和不为1，一定不符合；
显然B满足，故一定符合；
对于D，有，
又且，，所以它满足分布列的性质，
对于C，由于为实数，不妨取，显然，不满足概率的非负性，
而当时，满足分布列的性质，所以C不一定符合，
故选：C．
2.是离散型随机变量，，那么和分别是( )
A．B．
C．D．
【答案】D
【分析】由期望和方差的运算性质求解即可
【详解】由期望和方差的运算性质知E(X1)= E(2X－5)=2 E(X)-5=7
D(X1)= D(2X－5)= D(X)＝2
故选D
3.某商场销售某种品牌的空调，每周初购进一定数量的空调，商场每销售一台空调可获利500元，若供大于求，则每台未售出的空调需交保管费100元；若供不应求，则可从其他商场调剂供应，调剂的空调每台可获利200元．该商场记录了去年夏天（共10周）空调的周需求量n（单位：台），整理得表：
以10周记录的各需求量的频率作为各需求量发生的概率，若该商场周初购进20台空调，X表示当周的利润（单位：元），则当周的平均利润为（ ）
A．10000元B．9400元C．8800元D．9860元
【答案】D
【分析】求出X的可能取值，进而求出相应的概率，根据均值的计算公式即可求出结果.
【详解】当时，，
当时，，
则X的可能取值为8800，9400，10000，10200，10400，
，
，
，
，
，
则当周的平均利润
（元）．
故选：D．
【点睛】本题考查期望和方差的运算性质，熟记公式，准确计算是关键，是基础题
4.已知离散型随机变量X的分布列如下：
则其数学期望E(X)等于（ ）
A．1B．0.6C．2＋3mD．2.4
【答案】D
【分析】根据分布列的性质先求出m，再套用数学期望的公式即可求解
【详解】∵分布列中出现的所有的概率之和等于1，
∴解得
∴
故选：D
5.若随机变量的分布列为
且，则随机变量的方差等于A．B．C．D．
【答案】D
【详解】分析：先根据已知求出a,b的值，再利用方差公式求随机变量的方差.
详解：由题得
所以
故答案为D.
点睛：（1）本题主要考查分布列的性质和方差的计算，意在考查学生对这些知识的掌握水平.(2) 对于离散型随机变量，如果它所有可能取的值是，，…，，…，且取这些值的概率分别是，，…，，那么＝＋＋…＋,称为随机变量的均方差，简称为方差，式中的是随机变量的期望．
题型6两点分布
1.设随机变量服从两点分布，若，则成功概率（ ）
A．0.2B．0.4C．0.6D．0.8
【答案】C
【分析】根据两点分布概率性质可得解.
【详解】随机变量服从两点分布，，
根据两点分布概率性质可知：，
解得，
故选：C.
【点睛】本题考查了两点分布概率性质的简单应用，属于基础题.
2.随机变量服从两点分布，且，令，则（ ）
A．B．C．D．
【答案】D
【分析】根据两点分布的性质求出，则.
【详解】因为随机变量服从两点分布，且，
所以，
由，所以.
故选：D
3.下列关于随机变量及分布的说法正确的是（ ）
A．抛掷均匀硬币一次，出现正面的次数是随机变量
B．某人射击时命中的概率为0.5，此人射击三次命中的次数服从两点分布
C．离散型随机变量的分布列中，随机变量取各个值的概率之和可以小于1
D．离散型随机变量的各个可能值表示的事件是彼此互斥的
【答案】AD
【详解】对于选项A：抛掷均匀硬币一次，出现正面的次数可能是0，也可能是1，故是随机变量，故选项A正确；
对于选项B：某人射击时命中的概率为0.5，此人射击三次是三次独立重复实验，命中的次数服从二项分布而不是两点分布，故选项B错误；
对于选项C：离散型随机变量的分布列中，随机变量取各个值的概率之和一定等于1，故选项C错误；
对于选项D：由互斥事件的定义可知选项D正确．
故选：AD
【点睛】本题考查随机变量的概念、两点分布和二项分布的适用类型和离散型随机变量的取值及其概率；考查逻辑思维能力；属于基础题.
4.下列选项中的随机变量服从两点分布的是（ ）．
A．抛掷一枚骰子，所得点数X
B．某射手射击一次，击中目标得2分，未击中目标得0分，射手的得分X
C．从装有5个红球，3个白球的袋子中取1个球，定义：“取出白球”，“取出红球”
D．某医生做一次手术，手术成功的次数X
【答案】CD
【分析】利用两点分布的定义，逐项分析判断即可作答.
【详解】两点分布又叫0-1分布，试验结果只有两个，并且随机变量的取值只有0，1两个，C，D满足题意；
抛掷一枚骰子，所得点数X可能的结果为1，2，3，4，5，6，共6个，不是两点分布，A不满足题意；
某射手射击一次的试验结果有两个，但随机变量X的取值是0，2，B不满足题意．
故选：CD
5.有甲、乙两个盒子，甲盒子里有个红球，乙盒子里有个红球和个黑球，现从乙盒子里随机取出个球放入甲盒子后，再从甲盒子里随机取一球，记取到的红球个数为个，则随着的增加，下列说法正确的是（ ）
A．增加，增加B．增加，减小
C．减小，增加D．减小，减小
【答案】C
【分析】由题意可知，从乙盒子里随机取出个球，含有红球个数服从超几何分布，即，可得出，再从甲盒子里随机取一球，则服从两点分布，所以，，从而可判断出和的增减性.
【详解】由题意可知，从乙盒子里随机取出个球，含有红球个数服从超几何分布，即，其中，其中，且，.
故从甲盒中取球，相当于从含有个红球的个球中取一球，取到红球个数为.
故，
随机变量服从两点分布，所以，随着的增大，减小；
，随着的增大，增大.
故选：C.
【点睛】本题考查超几何分布、两点分布，分布列与数学期望，考查推理能力与计算能力，属于难题.
【能力提升】
单选题
1.设随机变量X等可能取值1，2，3，…n，如果，那么（ ）
A．B．C．D．不确定
【答案】C
【分析】根据随机变量的性质即可求解.
【详解】由于随机变量X等可能取值1，2，3，…n，所以，
由，所以，
故选：C
2.若某校研究性学习小组共6人，计划同时参观科普展，该科普展共有甲，乙，丙三个展厅，6人各自随机地确定参观顺序，在每个展厅参观一小时后去其他展厅，所有展厅参观结束后集合返回，设事件A为：在参观的第一小时时间内，甲，乙，丙三个展厅恰好分别有该小组的2个人；事件B为：在参观的第二个小时时间内，该小组在甲展厅人数恰好为2人，则（ ）．
A．B．C．D．
【答案】A
【分析】先求事件A包含的基本事件，再求事件AB包含的基本事件，利用公式可得.
【详解】由于6人各自随机地确定参观顺序，在参观的第一小时时间内，总的基本事件有个；事件A包含的基本事件有个；在事件A发生的条件下，在参观的第二个小时时间内，该小组在甲展厅人数恰好为2人的基本事件为个，而总的基本事件为，故所求概率为,故选A.
【点睛】本题主要考查条件概率的求解，注意使用缩小事件空间的方法求解.
3.从6名选手中，选取4个人参加奥林匹克竞赛，其中某甲被选中的概率是（ ）
A．B．C．D．
【答案】C
【分析】可计算基本事件的总数，再计算出所求概率事件含有的基本事件数，由公式可得概率．
【详解】从6人中选4人共有种选法，其中某甲被中的选法数为，
所以．
故选C．
4.元旦游戏中有20道选择题，每道选择题给了4个选项（其中有且只有1个正确）.游戏规定：每题只选1项，答对得2个积分，否则得0个积分.某人答完20道题，并且会做其中10道题，其它试题随机答题，则他所得积分X的期望值（ ）
A．25B．24C．22D．20
【答案】A
【分析】设剩余10题答对题目为道,则可表示出总的得分情况为.由二项分布可先求得,即可得所得积分X的期望值
【详解】设剩余10题答对题目为个,
有10道题目会做,则总得分为,且
由二项分布的期望可知
所以
故选:A
【点睛】本题考查了离散型随机变量的简单应用,二项分布的数学期望求法,属于中档题.
5.已知的分布列如表所示，其中a，b都是非零实数，则的最小值是（ ）
A．12B．6C．D．
【答案】B
【分析】由分布列的性质可得，利用结合基本不等式，即可求得答案.
【详解】根据分布列的性质知，．且，
所以，
当且仅当时等号成立,
故选:B．
6.设随机变量的概率分布列如表所示，则（ ）
A．B．C．D．
【答案】D
【分析】根据分布列概率之和为1，再根据的取值可求得答案.
【详解】因为，所以或，
所以或．
故选:D．
7.随机变量X所有可能取值是－2，0，3，5，且P(X＝－2)＝，P(X＝3)＝，P(X＝5)＝，则P(X＝0)的值为（ ）
A．0B．C．D．
【答案】C
【分析】根据随机变量各个变量概率和为1，即可求得答案.
【详解】由各个变量概率和为1可得：P(X＝－2)＋P(X＝0)＋P(X＝3)＋P(X＝5)＝1，
所以，解得
故选：C
8.已知随机变量的分布列为，则等于( )
A．B．C．D．
【答案】B
【分析】由分布列的性质求出的值，利用互斥事件概率的加法公式得，据此计算即得答案.
【详解】由，则，解得，
则.
故选：B
多选题
9.下列变量是随机变量的是（ ）
A．在某次数学期中考试中，一个考场30名考生中做对选择题第12题的人数
B．一台机器在一段时间内出现故障的次数
C．某体育馆共有6个出口，散场后从某一出口退场的人数
D．方程的实根个数
【答案】ABC
【分析】根据随机变量的定义判断即可求解.
【详解】随机变量的定义为：作一次实验，其结果有多种可能；选项ABC都符合随机变量的定义，故ABC都正确；
方程的实根个数是2，是确定的，不是随机变量，故D错误.
故选：ABC.
10.某市有四个景点，一位游客来该市游览，已知该游客游览的概率为，游览，和的概率都是，且该游客是否游览这四个景点相互独立，用随机变量 表示该游客游览的景点的个数，下列正确的（ ）
A．游客至多游览一个景点的概率为
B．
C．
D．
【答案】AB
【分析】根据题设确定随机变量X的可能取值，结合各选项的描述，结合对立、互斥事件概率及独立事件乘法公式求出对应，即可判断A、B、C，D.
【详解】解：由题意知，随机变量的可能取值为0，1，2，3，4，
A：游客至多游览一个景点，即游览0个或1个景点，即或，
，
，
游客至多游览1个景点概率为，正确；
B： ，正确；
C：，错误；
D：由于，故错误．
故选：AB．
11.(多选题)甲、乙两人下象棋，赢了得3分，平局得1分，输了得0分，共下三局.用表示甲的得分，则表示的可能结果为（ ）
A．甲赢三局
B．甲赢一局输两局
C．甲、乙平局三次
D．甲赢一局平两局
【答案】BC
【分析】列举出的所有可能的情况，由此得解.
【详解】甲、乙两人下象棋，赢了得3分，平局得1分，输了得0分，
所以有两种情况，即甲赢一局输两局或甲、乙平局三次．
故选：BC．
12.下列说法正确的是（ ）
A．若随机变量，则
B．若随机变量服从两点分布，且，则
C．若随机变量的分布列为，则
D．若随机变量，则的分布列中最大的只有
【答案】ABC
【分析】A选项，根据正态分布的对称性得到，A正确；B选项，根据服从两点分布，且得到分布列，求出的分布列，求出期望值和方差；C选项，根据概率之和为1列出方程，求出；D选项，根据解出答案.
【详解】A选项，，由正态分布的对称性可知，A正确；
B选项，若随机变量服从两点分布，且，
即分布列为：
所以
故，则，B正确；
C选项，分布列中概率之和为1，即，解得，C正确；
D选项，随机变量，令，
即，解得，
因为，所以或3，
则的分布列中最大的有或，D错误.
故选：ABC
填空题
13.设离散型随机变量X服从两点分布，若，则 ．
【答案】
【分析】直接根据两点分布的性质计算可得；
【详解】解：因为离散型随机变量X服从两点分布，且
所以
故答案为：
【点睛】本题考查两点分布的性质，属于基础题.
14.公司要从名男性员工和名女性员工中随机选出人去出差，设抽取的人中女性员工的人数为，则 .
【答案】
【分析】依题意可得，利用古典概型的概率公式计算可得.
【详解】依题意的可能取值为、、、，
所以.
故答案为：
15.现有7张卡片，分别写上数字1，2，3，4，5，5，6，从这7张卡片中随机抽取3张，记所取卡片上数字的最大值为X，则= ．
【答案】
【分析】根据给定条件，求出随机试验的基本事件总数，再求出的事件所含基本事件数即可计算作答.
【详解】从这7张卡片中随机抽取3张的试验有个基本事件，
其中的事件所含基本事件数为，
所以.
故答案为：
16.根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：
历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9，则工期延误天数Y的方差为 ．
【答案】9.8
【分析】求出Y的所有可能取值，进而求出相应的概率，列出分布列，再结合方差的计算公式即可求出结果.
【详解】由题意可知Y的所有可能取值0,2,6,10,
，
，
，
．
所以随机变量Y的分布列如下表所示：
所以，．
所以工期延误天数Y的方差为9.8．
故答案为：9.8.
解答题
17.有2件次品和3件正品混放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测结束．
(1)求第一次检测出的是次品且第二次检测出的是正品的概率；
(2)已知每检测一件产品需要费用100元，设X表示总检测费用（单位：元），求X的分布列．
【答案】(1)
(2)分布列见解析
【分析】（1）根据排列组合知识求出再次检测的基本事件总数与第一次检测出的是次品且第二次检测出的是正品这个事件含有的基本事件的方法数，然后计算概率；
（2）X的可能取值为200，300，400，分别求出概率可得分布列．
【详解】（1）设“第一次检测出的是次品且第二次检测出的是正品”为事件A，
则．
（2）X的可能取值为200，300，400，则，
，
．
故X的分布列为
18.某商场为了了解顾客的购物信息，随机在商场收集了位顾客购物的相关数据如下表：
统计结果显示位顾客中购物款不低于元的顾客占，该商场每日大约有名顾客，为了增加商场销售额度，对一次购物不低于元的顾客发放纪念品.（Ⅰ）试确定，的值，并估计每日应准备纪念品的数量；
（Ⅱ）为了迎接春节，商场进行让利活动，一次购物款元及以上的一次返利元；一次购物不超过元的按购物款的百分比返利，具体见下表：
请问该商场日均大约让利多少元？
【答案】(1)2400;(2)41600.
【详解】试题分析：（Ⅰ）由位顾客中购物款不低于元的顾客可得，，从而可得，进而得商场每日应准备纪念品的数量大约为；（Ⅱ）先算出各购物消费区间的人数，利用各区间中点值乘以对应的人数及返利比例，求和可得到该商场日均大约让利费用.
试题解析：（Ⅰ）由已知，100位顾客中购物款不低于150元的顾客有，；
.
该商场每日应准备纪念品的数量大约为.
（Ⅱ）设顾客一次购物款为元.
当时，顾客约有人；
当时，顾客约有人；
当时，顾客约有人；
当时，顾客约有人.
该商场日均大约让利为：
（元）.
19.今年雷锋日，某中学从高中三个年级中选派4名教师和20名学生去当雷锋志愿者，学生的名额分配如下：
(1)若从20名学生中选出3人参加文明交通宣传，记X为抽取的3人中高一年级学生的人数，求随机变量X的分布列；
(2)若将4名教师安排到三个年级（假设每名教师加入各年级是等可能的，且各位教师的选择是相互独立的），记安排到高一年级的教师人数为，求随机变量的分布列.
【答案】(1)分布列见解析
(2)分布列见解析
【分析】（1）先求出的可能取值为：0，1，2，3，再分别求概率即可；
（2）先求出的可能取值为：0，1，2，3，4，再分别求概率即可．
【详解】（1）由题意易知的可能取值为：0，1，2，3，
则，，，
则X的分布列为：
（2）由题意易知的可能取值为：0，1，2，3，4，
则，，，，
则的分布列为：
20.是指悬浮在空气中的空气动力学当量直径小于或等于微米的颗粒物，也称为可入肺颗粒物.根据现行国家标准，日均值在微克/立方米以下，空气质量为一级；在微克应立方米微克立方米之间，空气质量为二级：在微克/立方米以上，空气质量为超标.从某市年全年每天的监测数据中随机地抽取天的数据作为样本，监测值频数如下表：
（1）从这天的日均值监测数据中，随机抽出天，求恰有天空气质量达到一级的概率；
（2）从这天的数据中任取天数据，记表示抽到监测数据超标的天数，求的分布列.
【答案】（1）；（2）分布列见解析.
【分析】（1）由表格可知：这天的日均值监测数据中，只有天达到一级，然后利用组合计数原理与古典概型的概率公式可计算出所求事件的概率；
（2）由题意可知，随机变量的可能取值有、、、，然后利用超几何分布即可得出随机变量的分布列.
【详解】（1）由表格可知：这天的日均值监测数据中，只有天达到一级．
随机抽取天，恰有天空气质量达到一级的概率为；
（2）由题意可知，随机变量的可能取值有、、、，
，，，.
因此，随机变量的分布列如下表所示：
【点睛】本题考查了概率的计算，同时也考查了超几何分布及其分布列等基础知识与基本技能，属于中档题．
21.某校为了提高教师身心健康号召教师利用空余时间参加阳光体育活动.现有名男教师，名女教师报名，有慢跑、游泳、瑜伽三个可选项目，本周随机选取人参加，每名女教师至多从中选择参加项活动，且选择参加项或项的可能性均为；每名男教师至少从中选择参加项活动，且选择参加项或项的可能性也均为.每人每参加项活动可获得“体育明星” 积分分，选择参加几项活动彼此互不影响，求：
(1)在有女教师参加活动的条件下，恰有一名女教师参加活动的概率；
(2)记随机选取的两人得分之和为，参加活动的女教师人数为，
（i）求与的关系；
（ii）求两人得分之和的数学期望.
【答案】(1)
(2)（i）；（ii）42.5
【分析】（1）由条件概率的计算公式即可求解，
（2）根据一名女教师以及一名男教师参加活动获得分数的期望，即可得，利用的分布列即可求解,由期望的性质即可得，或者利用分类加法以及概率乘法公式也可求解分布列,进而由期望公式求解.
【详解】（1）记有女教师参加活动为事件A，恰有1名女教师参加活动为事件B
，
，
故在有女教师参加活动的条件下，恰有1名女教师参加活动概率为
（2）根据题意，一名女教师参加活动可获得分数的期望为，
一名男教师参加活动可获得分数的期望为
设恰有Y名女教师参加活动，则男教师有名参加活动，
，
则，，．
所以Y的分布列为
则有，
所以．
法二：设恰有Y名女教师参加活动，则男教师有名参加活动，
则，，．
22.已知一个袋中装有个白球和个红球，这些球除颜色外完全相同.
（1）每次从袋中取一个球，取出后不放回，直到取到一个红球为止，求取球次数的分布列和数学期望；
（2）每次从袋中取一个球，取出后放回接着再取一个球，这样取次，求取出红球次数的分布列、数学期望和方差.
【答案】（1）分布列见解析；期望为；（2）分布列见解析；，.
【解析】（1）取到一个红球为止，取球次数所有可能、、、，求对应次数的概率即可列分布列，求；
（2）取出后放回，每次取到红球的概率相同，相当于做了三次独立重复试验，利用二项分布概率公式和期望、方差公式即可求解.
【详解】（1）的可能取值为、、、，
，，
，，
故的分布列为：
；
（2）取出后放回，取球次，每次取到红球的概率为，可看作次独立重复试验，所以，
的可能取值为、、、，
，，
，，
故的分布列为：
∴，
.
【点睛】思路点睛：求离散型随机变量的分布列及期望的一般步骤：
（1）根据题中条件确定随机变量的可能取值；
（2）求出随机变量所有可能取值对应的概率，即可得出分布列；
（3）根据期望的概念，结合分布列，即可得出期望（在计算时，要注意随机变量是否服从特殊的分布，如超几何分布或二项分布等，可结合其对应的概率计算公式及期望计算公式，简化计算）
X
1
2
P
X
0
1
P
X
0
1
2
P
X
0
1
2
P
X
P
1
2
3
4
0
1
2
3
4
0.1
0.2
0.3
0.1
0
1
ξ
1
2
3
4
P

m
n
X
0
1
P
周需求量n
18
19
20
21
22
频数
1
2
3
3
1
X
1
3
5
P
0.5
m
0.2
1
2
3
4
P
a
b
2
3
4
0
1
0
2
降水量X
工期延误天数Y
0
2
6
10
Y
0
2
6
10
P
0.3
0.4
0.2
0.1
X
200
300
400
P
一次购物款（单位：元）
顾客人数
一次购物款（单位：元）
返利百分比
高一年级
高二年级
高三年级
10人
6人
4人
0
1
2
3
0
1
2
3
4
日均值
（微克/立方米）
频数（天）
Y
0
1
2
P

20
30
40
50
60